Mathématiques Terminale Spécialité
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Rappels de première
Algèbre et géométrie
Ch. 1
Combinatoire et dénombrement
Ch. 2
Vecteurs, droites et plans de l’espace
Ch. 3
Orthogonalité et distances dans l’espace
Analyse
Ch. 4
Suites
Ch. 5
Limites de fonctions
Ch. 6
Continuité
Ch. 7
Compléments sur la dérivation
Ch. 8
Logarithme n�épérien
Ch. 9
Fonctions trigonométriques
Ch. 10
Primitives - Équations différentielles
Ch. 11
Calcul intégral
Probabilités
Ch. 12
Loi binomiale
Ch. 13
Sommes de variables aléatoires
Ch. 14
Loi des grands nombres
Annexes
Exercices transversaux
Grand Oral
Apprendre à démontrer
Cahier d'algorithmique et de programmation
Chapitre 14
Objectif BAC
Exercices de synthèse
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
82
Python
[Modéliser, Chercher.]
Un célèbre jeu télévisé propose aux candidats l'expérience suivante, où trois boîtes sont disposées devant le joueur. Deux boîtes sont vides et une contient de l'argent. Le candidat commence par en choisir une au hasard. Le présentateur, qui connaît la répartition des lots, retire alors une boîte vide parmi les deux restantes et demande ensuite au joueur s'il garde son premier choix, ou s'il souhaite changer de boîte.
Deux amis regardent ce jeu et discutent entre eux.
Anthony pense que, puisqu'il reste uniquement deux boîtes, chacune offre autant de chance de gagner.
Laura pense qu'il vaut mieux changer car l'élimination d'une boîte laisse 2 chances sur 3 de gagner si l'on change de boîte. 1. On suppose (pour simplifier) qu'on choisit la boîte numéro 1. Énoncer toutes les situations possibles et montrer alors que Laura a raison.
2. Malgré cette preuve, Anthony n'est toujours pas convaincu. Il propose alors la chose suivante : « J'ai vu dans mon cours que, si on répète l'expérience un grand nombre de fois, la fréquence obtenue tend vers la probabilité ».
Proposer un algorithme pour simuler cette expérience.
3. Simuler l'expérience un très grand nombre de fois et montrer que le résultat conforte l'idée de Laura.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
83
Démo
[Raisonner, Chercher.]
Une variante de la loi faible des grands nombres
On considère une suite de variables aléatoires indépendantes (\text{X}_n), où n est un entier naturel strictement positif. On suppose que chaque variable aléatoire \mathrm{X}_{n} suit une loi de Bernoulli de paramètre p_n (les paramètres ne sont pas nécessairement égaux pour toutes les valeurs de n).On pose \mathrm{S}_{n}=\mathrm{X}_{1}+\mathrm{X}_{2}+\ldots+\mathrm{X}_{n}.
1. On veut montrer que, pour tout \varepsilon\gt0 : \lim\limits_{n \rightarrow+\infty} \mathrm{P}\left(\left|\frac{\mathrm{S}_{n}}{n}-\frac{1}{n} \sum\limits_{i=1}^{n} p_{i}\right| \geqslant \varepsilon\right)=0.
a. Pourquoi n'est-il pas possible d'appliquer la loi des grands nombres ici ?
b. Déterminer l'espérance et la variance de \mathrm{S}_{n} puis montrer que, pour tout entier n \gt 0, \text{V}\left(\text{S}_{n}\right) \leqslant n.
a. Pourquoi n'est-il pas possible d'appliquer la loi des grands nombres ici ?
b. Déterminer l'espérance et la variance de \mathrm{S}_{n} puis montrer que, pour tout entier n \gt 0, \text{V}\left(\text{S}_{n}\right) \leqslant n.
c. En appliquant convenablement l'inégalité de Bienaymé-Tchebychev, montrer le résultat souhaité.
2. Dans ce cas bien précis d'une somme de variables aléatoires suivant une loi de Bernoulli, qu'apporte ce résultat en plus, par rapport à la loi des grands nombres étudiée dans le cours ?
2. Dans ce cas bien précis d'une somme de variables aléatoires suivant une loi de Bernoulli, qu'apporte ce résultat en plus, par rapport à la loi des grands nombres étudiée dans le cours ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
84
Python
[Modéliser, Chercher.]
On cherche à modéliser une expérience aléatoire dont l'ensemble des issues serait infini. 1. Soit n un entier naturel.
a. Montrer que, pour tout n \in \mathbb{N}, 0 \leqslant \frac{1}{\mathrm{e} \times n !} \leqslant 1.
b. Ecrire un programme Python pour simuler la somme \mathrm{S}_{n}=\sum\limits_{k=0}^{n} \frac{1}{\mathrm{e} \times k !}.
c. Tester le programme pour n = 100 et n = 1\:000.
d. Que remarque-t-on ?
La loi de la variable aléatoire définie pour tout n \in \mathbb{N} par \mathrm{P}(\mathrm{X}=n)=\frac{1}{\mathrm{e} \times n !}, est appelée loi de Poisson de paramètre 1.
2. Faire le même travail avec la variable \text{Y} telle que \mathrm{P}(\mathrm{Y}=n)=\left(\frac{1}{4}\right)^{n} \times \frac{3}{4} (loi géométrique de paramètre \frac{3}{4}).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
85
Approfondissement
On souhaite réaliser un sondage sur le nombre d'hommes et de femmes dans la société française. Pour cela, un statisticien décide d'engager une étude autour des nouveau- nés. Il obtient le tableau suivant.

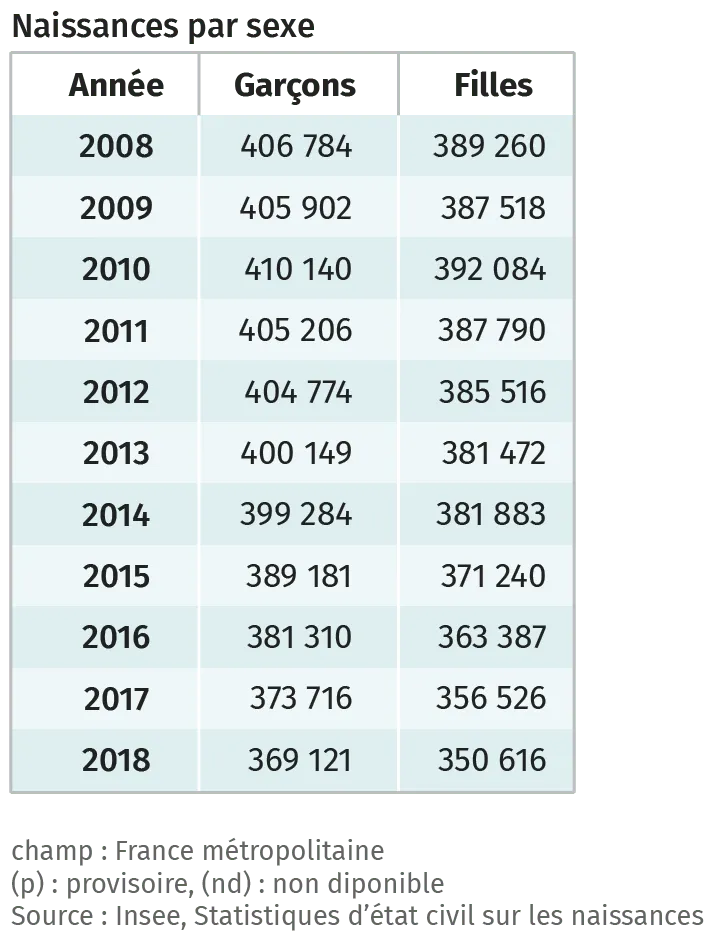
On définit le sex ratio, noté \text{SR}, par la relation suivante : \mathrm{SR}=\frac{\text { Nombre d'hommes }}{\text { Nombre de femmes }}.


On définit le sex ratio, noté \text{SR}, par la relation suivante : \mathrm{SR}=\frac{\text { Nombre d'hommes }}{\text { Nombre de femmes }}.
1. Calculer le sex ratio pour les années 2008 à 2018.
Ce nombre semble-t-il stable ?
2. On suppose dans cette question qu'on dispose seulement de la moyenne des \text{SR} des années 2009 à 2018.
a. En calculant cette valeur, expliquer comment en déduire la proportion moyenne d'hommes dans la population française et donner cette valeur.
b. En justifiant soigneusement, quel nombre peut-on considérer pour estimer la proportion d'hommes dans la population française ?
3. Dans cette question, on cherche à déterminer le nombre de personnes n à étudier pour avoir une précision souhaitée. On considère la variable aléatoire \mathrm{M}_{n}=\sum\limits_{i=1}^{n} \frac{\mathrm{X}_{i}}{n}, où \mathrm{X}_{i} = 1 si la personne interrogée est une femme et \mathrm{X}_{i} = 0 si la personne interrogée est un homme. En reprenant l'estimation obtenue à la question précéde, déterminer n pour que \mathrm{P}\left(\left|\mathrm{M}_{n}-\mathrm{E}\left(\mathrm{M}_{n}\right)\right| \geqslant 0{,}1\right)\lt0{,}05.
2. On suppose dans cette question qu'on dispose seulement de la moyenne des \text{SR} des années 2009 à 2018.
a. En calculant cette valeur, expliquer comment en déduire la proportion moyenne d'hommes dans la population française et donner cette valeur.
b. En justifiant soigneusement, quel nombre peut-on considérer pour estimer la proportion d'hommes dans la population française ?
3. Dans cette question, on cherche à déterminer le nombre de personnes n à étudier pour avoir une précision souhaitée. On considère la variable aléatoire \mathrm{M}_{n}=\sum\limits_{i=1}^{n} \frac{\mathrm{X}_{i}}{n}, où \mathrm{X}_{i} = 1 si la personne interrogée est une femme et \mathrm{X}_{i} = 0 si la personne interrogée est un homme. En reprenant l'estimation obtenue à la question précéde, déterminer n pour que \mathrm{P}\left(\left|\mathrm{M}_{n}-\mathrm{E}\left(\mathrm{M}_{n}\right)\right| \geqslant 0{,}1\right)\lt0{,}05.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
86
Python
Approfondissement
Un professeur oublie fréquemment les clefs de sa salle de classe. S'il oublie ses clefs le jour n, la probabilité qu'il les oublie le lendemain est de 0{,}1. S'il n'oublie pas ses clefs le jour n, la probabilité qu'il les oublie le lendemain est de 0{,}4.
La probabilité qu'il les oublie le premier jour est de 0{,}2.
On considère, pour tout entier naturel n non nul, l'événement \text{E}_n\:: « Le professeur oublie ses clefs le jour n. » et on note p\left(\mathrm{E}_{n}\right)=p_{n}.
Partie A :
1. Calculer p_1, p_2 et p_3.2. Déterminer une relation de récurrence entre p_{n+1} et p_n pour tout entier n \gt 0.
3. Pour tout entier n \gt 0, on pose u_{n}=p_{n}+\alpha. Déterminer \alpha pour que (\text{U}_n) soit géométrique.
4. Exprimer u_n puis p_n en fonction de n.
5. Déterminer la limite de la suite (p_n) et en donner l'interprétation.
Partie B :
On suppose qu'un élève arrive uniquement à répondre aux questions 1. et 2. de la partie A. Il décide donc d'entreprendre une démarche numérique pour répondre aux questions suivantes.1. Écrire un algorithme qui permette de calculer les n premiers termes de la suite (p_n).
2. Programmer et tester l'algorithme avec Python pour plusieurs (grandes) valeurs de n.
3. Quelle semble être la limite de la suite (p_n) ? Ce résultat est-il cohérent avec le résultat de la partie A ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercices transversaux en lien avec ce chapitre :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le Grand Oral
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Justifier le lien entre votre sujet et votre projet d'orientation
Exemple de sujet : Les sondages d'opinion
Méthode
❯ Le sujet que vous avez choisi de présenter doit être en lien avec votre projet d'études.❯ Le jury va s'intéresser à ce que le travail sur votre sujet vous a permis de découvrir et éventuellement de confirmer par rapport à votre projet d'orientation.
❯ Pour anticiper cette dernière partie de l'épreuve, posez-vous les questions suivantes : Qu'est-ce que la préparation du Grand Oral et le travail sur mon sujet m'ont appris ? Quels aspects du métier ou du domaine dans lequel je souhaite me former ai-je pu approfondir ? Certains points m'ont-ils surpris, déçu, intrigué ?
Exemples de liens avec un projet d'orientation
❯ N'hésitez pas à présenter les méthodes ainsi que les particularités des instituts de sondage que vous avez pu étudier.❯ Les sondages sont très utilisés dans le domaine politique mais c'est également un outil essentiel dans le marketing pour déterminer la satisfaction ou les attentes des clients par exemple.
❯ Ce sujet peut également vous permettre d'aborder l'analyse de données (via des méthodes statistiques) où les applications sont nombreuses.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
