Mathématiques Terminale Spécialité
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Rappels de première
Algèbre et géométrie
Ch. 1
Combinatoire et dénombrement
Ch. 2
Vecteurs, droites et plans de l’espace
Ch. 3
Orthogonalité et distances dans l’espace
Analyse
Ch. 4
Suites
Ch. 5
Limites de fonctions
Ch. 6
Continuité
Ch. 7
Compléments sur la dérivation
Ch. 8
Logarithme n�épérien
Ch. 9
Fonctions trigonométriques
Ch. 10
Primitives - Équations différentielles
Ch. 11
Calcul intégral
Probabilités
Ch. 12
Loi binomiale
Ch. 13
Sommes de variables aléatoires
Ch. 14
Loi des grands nombres
Annexes
Exercices transversaux
Grand Oral
Apprendre à démontrer
Cahier d'algorithmique et de programmation
Chapitre 12
Cours 3
Introduction à l'échantillonnage
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
Soient n un entier naturel non nul, \alpha et p deux nombres réels appartenant à [0~; 1] et \text{X} une variable aléatoire qui suit la loi binomiale \mathcal{B}(n~; p).
Il existe un intervalle \text{I} non vide tel que \mathrm{P}(\mathrm{X} \in \mathrm{I}) \geqslant 1-\alpha.
Il existe un intervalle \text{I} non vide tel que \mathrm{P}(\mathrm{X} \in \mathrm{I}) \geqslant 1-\alpha.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Cette propriété démontre l'existence d'un intervalle qui convient mais cet intervalle n'est pas unique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
L'intervalle \mathrm{I}=[0~; n] convient. En effet, pour tout \alpha \in[0~; 1], 1-\alpha \leqslant 1 et \mathrm{P}(0 \leqslant \mathrm{X} \leqslant n)=1 donc on a bien \mathrm{P}(\mathrm{X} \in \mathrm{I}) \geqslant 1-\alpha.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- La suite \left(u_{k}\right) de terme général u_{k}=\mathrm{P}(\mathrm{X} \leqslant k) est croissante et, à partir d'un certain rang, ses termes valent tous 1.
- Dans la pratique, on cherchera souvent un intervalle dont l'amplitude est la plus petite possible.
- Selon le contexte, l'intervalle est généralement de la forme [0~; k], [k~; n] ou [k~; k'].
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode - 4
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
On considère la variable aléatoire \text{X} qui suit la loi binomiale \mathcal{B}(n~; p) avec n=40 et p=0{,}38.
Dans chaque cas, déterminer les entiers a ou b vérifiant \mathrm{P}(a \leqslant \mathrm{X} \leqslant b) \geqslant 0{,}95 et la condition donnée.
1. On pose a = 0 et on cherche le plus petit entier b qui puisse convenir.
2. On pose b = 40 et on cherche le plus grand entier a qui puisse convenir.
3. On cherche l'intervalle [a~; b] de plus petite amplitude possible tel que \mathrm{P}(\mathrm{X} \leqslant a) \approx \mathrm{P}(\mathrm{X} \geqslant b) (arrondir à 10^{-2} près).
1. On pose a = 0 et on cherche le plus petit entier b qui puisse convenir.
2. On pose b = 40 et on cherche le plus grand entier a qui puisse convenir.
3. On cherche l'intervalle [a~; b] de plus petite amplitude possible tel que \mathrm{P}(\mathrm{X} \leqslant a) \approx \mathrm{P}(\mathrm{X} \geqslant b) (arrondir à 10^{-2} près).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. On remarque que \mathrm{P}(0 \leqslant \mathrm{X} \leqslant b)=\mathrm{P}(\mathrm{X} \leqslant b) puis on utilise la calculatrice pour obtenir la valeur de b souhaitée.
2. On remarque que \mathrm{P}(a \leqslant \mathrm{X} \leqslant n)=\mathrm{P}(\mathrm{X} \geqslant a) puis on utilise à nouveau la calculatrice.
3. On s'aide des questions 1. et 2. pour faire des tests à la calculatrice et trouver un intervalle qui convient.
2. On remarque que \mathrm{P}(a \leqslant \mathrm{X} \leqslant n)=\mathrm{P}(\mathrm{X} \geqslant a) puis on utilise à nouveau la calculatrice.
3. On s'aide des questions 1. et 2. pour faire des tests à la calculatrice et trouver un intervalle qui convient.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
En utilisant une calculatrice ou un tableur, on peut rapidement obtenir les valeurs de certaines probabilités.

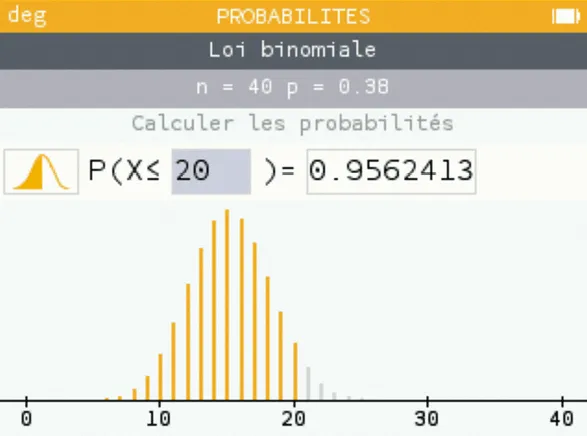

1. On lit \mathrm{P}(\mathrm{X} \leqslant 19) \approx 0{,}918 et \mathrm{P}(\mathrm{X} \leqslant 20) \approx 0{,}956 donc avec a = 0 et b = 20, on a \mathrm{P}(a \leqslant \mathrm{X} \leqslant b) \geqslant 0{,}95.
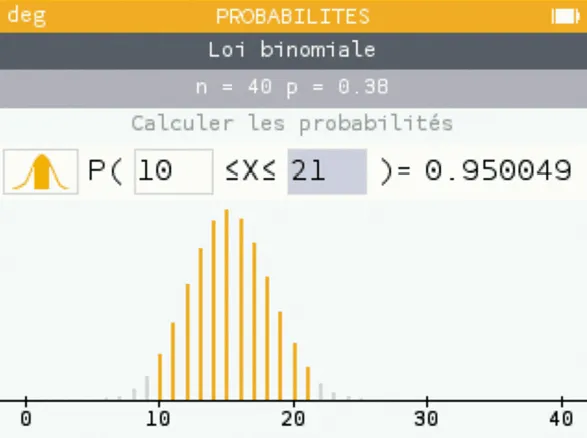
2. On lit \mathrm{P}(\mathrm{X} \geqslant 10) \approx 0{,}971 et \mathrm{P}(\mathrm{X} \geqslant 11) \approx 0{,}940 donc avec a = 10 et b = 40, on a \mathrm{P}(a \leqslant \mathrm{X} \leqslant b) \geqslant 0{,}95.
3. Avec a = 8 et b = 23, on a \mathrm{P}(a \leqslant \mathrm{X} \leqslant b) \approx 0{,}992, \mathrm{P}(\mathrm{X} \leqslant a) \approx 0{,}01 et \mathrm{P}(\mathrm{X} \geqslant b) \approx 0{,}01.
On a donc bien \mathrm{P}(a \leqslant \mathrm{X} \leqslant b) \geqslant 0{,}95 et \mathrm{P}(\mathrm{X} \leqslant a) \approx \mathrm{P}(\mathrm{X} \geqslant b).




1. On lit \mathrm{P}(\mathrm{X} \leqslant 19) \approx 0{,}918 et \mathrm{P}(\mathrm{X} \leqslant 20) \approx 0{,}956 donc avec a = 0 et b = 20, on a \mathrm{P}(a \leqslant \mathrm{X} \leqslant b) \geqslant 0{,}95.
2. On lit \mathrm{P}(\mathrm{X} \geqslant 10) \approx 0{,}971 et \mathrm{P}(\mathrm{X} \geqslant 11) \approx 0{,}940 donc avec a = 10 et b = 40, on a \mathrm{P}(a \leqslant \mathrm{X} \leqslant b) \geqslant 0{,}95.
3. Avec a = 8 et b = 23, on a \mathrm{P}(a \leqslant \mathrm{X} \leqslant b) \approx 0{,}992, \mathrm{P}(\mathrm{X} \leqslant a) \approx 0{,}01 et \mathrm{P}(\mathrm{X} \geqslant b) \approx 0{,}01.
On a donc bien \mathrm{P}(a \leqslant \mathrm{X} \leqslant b) \geqslant 0{,}95 et \mathrm{P}(\mathrm{X} \leqslant a) \approx \mathrm{P}(\mathrm{X} \geqslant b).
Pour s'entraîner
Exercices , et
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
