Activités

« Lettre à un amy, sur les parties du jeu de paume » est une lettre publiée en 1713 dans l’Ars Conjectandi. Jacques Bernoulli y donne, entre autres, les probabilités de gagner lors d’une partie de jeu de paume, ancêtre de notre tennis moderne. Cette lettre donne des résultats mathématiques concrets appliqués à la vie de tous les jours et s’éloigne de documents mathématiques très théoriques.
À noter que la façon de compter les points au jeu de paume est la même qu’au tennis, sauf qu’après avoir gagné un troisième échange, on comptabilise 45 points et non 40 comme au tennis.

Partie A

Deux joueurs A et B de même force jouent ensemble.
La table de Bernoulli ci-dessous donne les probabilités de gagner du joueur A en fonction du score.

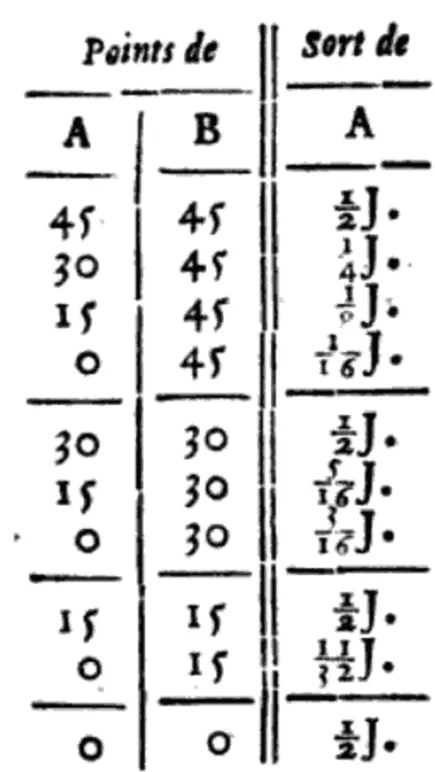
Par exemple, sur un score de 15-30, le joueur A a une probabilité de $\dfrac{5}{16}$ de gagner, ce qui est noté $\dfrac{5}{16}\text{J}.$
Même si, pour gagner, il faut avoir 2 points de plus que son adversaire, on admet que les joueurs étant de même force, ils ont chacun une chance sur deux de gagner.

Expliquer pourquoi, sur un score de 45-45 (chaque joueur a 45 points), le joueur A a une chance sur deux de gagner.


Score de 30-45 : le joueur A a 30 points et le joueur B a 45 points.
a) Quelle est la probabilité pour le joueur A de revenir au score 45-45 ?


b) Montrer que dans ce cas, la probabilité que A a de gagner est bien $\dfrac{1}{4}\text{J}.$


Score de 15-45 : le joueur A a 15 points et le joueur B a 45 points.
a) Quelle est la probabilité pour le joueur A de revenir au score 30-45 ?


b) Montrer que, dans ce cas, la probabilité que A a de gagner est bien $\dfrac{1}{8}\text{J}.$


En s’inspirant des réponses aux questions précédentes et en travaillant de proche en proche, montrer que pour un score de 15-30, la probabilité que A a de gagner est $\dfrac{5}{16}\text{J}.$

Partie B

Jacques Bernoulli répond également au problème suivant : si A est n fois plus fort que B, quelles sont alors ses probabilités de gagner ?
Autrement dit, le joueur A marque le point avec une probabilité égale à $\dfrac{n}{n+1}.$

Score de 45-45. On rappelle qu’il faut deux points d’écart à un joueur pour gagner.
a) Démontrer que le joueur A gagne avec la probabilité indiquée par Bernoulli de $\dfrac{n^{2}}{n^{2}+1}.$


b) Quelle probabilité le joueur B a-t-il de gagner ?


Score de 30-45.
a) Quelle est la probabilité pour le joueur A de revenir au score 45-45 ?


b) Montrer que, dans ce cas, la probabilité que A a de gagner est bien $\dfrac{n^{3}}{n^{3}+n^{2}+n+1}$ (attention, il y a une erreur dans l’impression du livre de l’époque).


En procédant de proche en proche, on retrouve alors toutes les probabilités établies par Jacques Bernoulli.

Jacques Bernoulli est le premier à aborder le problème du lien qui existe entre les probabilités d’un événement et les fréquences de sa réalisation. Dans Ars Conjectandi (1713), au chapitre IV de la 4^e partie, il explique que l’on peut également mesurer une probabilité à partir de fréquences de réalisation d’une expérience aléatoire. Au chapitre V, il met en oeuvre ce qu’il vient d’énoncer. Dans une urne qui contient $t$ boules dont $r$ boules blanches (fertiles), il effectue $n \times t$ tirages avec remise et compte le nombre de boules blanches. Et il écrit :

Jacques Bernoulli, Ars Conjectandi, 4^e partie, traduction du Latin par Norbert Meunier.

On appelle $\text{F}$ la fréquence observée et $p$ la probabilité de l’événement « La boule tirée est blanche ».
Le nombre $c$ dont parle Bernoulli est le nombre minimum de tirages nécessaires pour avoir, en termes actuels, $\mathrm{P}\left(\mathrm{F}-\dfrac{1}{t} \lt p \lt \mathrm{F}+\dfrac{1}{t}\right) \gt 1-\alpha$ où $\alpha$ est un réel de $[0 \:; 1]$ fixé. Bernoulli en effectue une formidable démonstration se basant sur les résultats qu’il venait de démontrer sur la loi binomiale.
Près de 150 ans plus tard, Bienaymé et Tchebychev publient l’inégalité qui porte leur nom. Ils fournissent ainsi une démonstration plus simple de la loi des grands nombres qui, de plus, permet de lier la probabilité de réalisation d’une variable aléatoire à son espérance et à sa variance.

Soit $n \in \N.$ On note $\text{I}$ l’ensemble des entiers naturels strictement positifs et inférieurs ou égaux à $n$ ; autrement dit, $\mathrm{I}=\mathbb{N} \cap[1 \:; n].$
Soit $\text{X}$ la variable aléatoire qui prend les valeurs positives $x_i$ pour $i \in \text{I}$ de probabilités respectives $p_i.$
On pose $m = \text{E(X)}$ et on note $\text{V(X)}$ la variance de $\text{X}$.

Compléter l'égalité suivante : $\mathrm{V}(\mathrm{X})=\sum\limits_{i \in \mathrm{I}}(\ldots)$.


Soit $\text{J}$ l’ensemble des entiers $i$ tels que $1 \leqslant i \leqslant n$ et $\left|x_{i}-m\right| \geqslant \alpha.$ On a donc $\mathrm{J}=\left\{i \in \mathrm{I} /\left|x_{i}-m\right| \geqslant \alpha\right\}.$ Justifier que $\mathrm{V}(\mathrm{X}) \geqslant \sum\limits_{i \in \mathrm{J}}\left(x_{i}-m\right)^{2} p_{i}.$


Montrer que $\sum\limits_{i \in \mathrm{J}} \alpha^{2} p_{i}=\alpha^{2} \mathrm{P}(|\mathrm{X}-m| \geqslant \alpha).$


En utilisant $\left|x_{i}-m\right| \geqslant \alpha,$ donner une minoration de $\text{V(X)}$ et en déduire l’inégalité de Bienaymé-Tchebychev : $\mathrm{P}(|\text{X}-m| \geqslant \alpha) \leqslant \dfrac{\mathrm{V}(\mathrm{X})}{\alpha^{2}}.$

Vous trouverez la démonstration complète — longue mais faisable — de Tchebychev à la page 178 du journal de mathématiques pures et appliquées sur le site de Gallica.