Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Rappels de première
Algèbre et géométrie
Ch. 1
Combinatoire et dénombrement
Ch. 2
Vecteurs, droites et plans de l’espace
Ch. 3
Orthogonalité et distances dans l’espace
Analyse
Ch. 4
Suites
Ch. 5
Limites de fonctions
Ch. 6
Continuité
Ch. 7
Compléments sur la dérivation
Ch. 8
Logarithme népérien
Ch. 9
Fonctions trigonométriques
Ch. 10
Primitives - Équations différentielles
Ch. 11
Calcul intégral
Probabilités
Ch. 12
Loi binomiale
Ch. 13
Sommes de variables aléatoires
Ch. 14
Loi des grands nombres
Annexes
Exercices transversaux
Grand Oral
Apprendre à démontrer
Cahier d'algorithmique et de programmation
Chapitre 12
TP INFO 1
Planche de Galton
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Un joueur lâche une bille sur une planche inclinée sur laquelle sont plantés des clous comme sur la figure ci‑contre. À chaque clou rencontré, la bille passe indifféremment à droite ou à gauche de façon équiprobable. En fin de parcours, elle tombe dans une case. Le numéro de la case est donc le nombre de fois où la bille est descendue à droite lors de son parcours.
Dans ce TP, on considère une planche de Galton à douze rangées de clous ; il y a donc 13 cases numérotées de 0 (case à gauche) à 12 (case à droite).
On suppose qu'à chaque clou, la probabilité d'aller à droite est égale à 0{,}5.
On suppose qu'à chaque clou, la probabilité d'aller à droite est égale à 0{,}5.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions pr éliminaires
1. Soit \text{X} la variable aléatoire donnant la case dans laquelle une bille donnée finit sa chute. Déterminer la loi de probabilité suivie par \text{X}.
2. Quelle est la probabilité qu'une bille finisse dans la case de gauche ? Dans la case n°11 ? Dans la case n°6 ?
3. Quelle est l'espérance de \text{X} ? Interpréter le résultat dans le contexte.
2. Quelle est la probabilité qu'une bille finisse dans la case de gauche ? Dans la case n°11 ? Dans la case n°6 ?
3. Quelle est l'espérance de \text{X} ? Interpréter le résultat dans le contexte.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Simuler la chute de 1 000 billes le long de cette planche et vérifier que la simulation est bien cohérente avec la théorie.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1Python
1. Créer une fonction direction qui renvoie la direction prise par une bille lors du passage d'une rangée (0 pour gauche et 1 pour droite).
2. On souhaite simuler la chute de 1 000 billes en créant une fonction qui renvoie une liste, chaque indice de la liste correspondant à une case et la valeur correspondant au nombre de billes présentes dans la case à la fin de la simulation. Par exemple :
from random import randint def direction() : return ...
2. On souhaite simuler la chute de 1 000 billes en créant une fonction qui renvoie une liste, chaque indice de la liste correspondant à une case et la valeur correspondant au nombre de billes présentes dans la case à la fin de la simulation. Par exemple :
Le zoom est accessible dans la version Premium.
En reprenant votre fonction direction, compléter la fonction simulation.
3. Exécuter le programme et vérifier, pour 1 000 billes, que la simulation est en accord avec les résultats calculés dans les questions préliminaires.
from random import randint
def direction() :
return ...
def simulation(n):
#liste correspondant aux 13 cases
cases = 13*[0]
for bille in range (...):
case_finale = 0
for clou in range(...):
case_finale = case_finale + ...
cases[case_finale] = cases[case_finale] + 1
return cases
3. Exécuter le programme et vérifier, pour 1 000 billes, que la simulation est en accord avec les résultats calculés dans les questions préliminaires.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Tableur
1. Reproduire la feuille de calcul suivante.
Le zoom est accessible dans la version Premium.
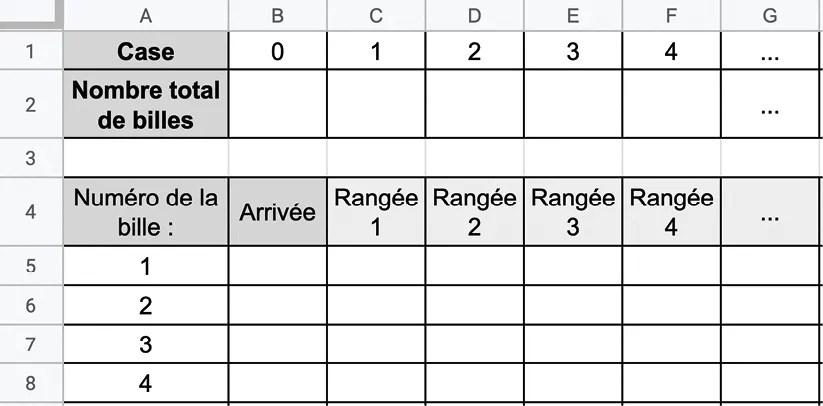
2. On s'intéresse à la trajectoire de la première bille.
a. Remplir les cellules C5 à N5 pour obtenir une série aléatoire de douze 0 et 1. 0 indique que la bille va à gauche et 1 qu'elle va à droite.
b. Quelle formule doit‑on entrer dans la cellule B5 pour obtenir la valeur de la case d'arrivée de la bille ?
3. a. Simuler la chute de 1 000 billes.
b. Utiliser la ligne 2 pour compter le nombre de billes dans chacune des cases d'arrivée.
c. Les résultats obtenus à l'aide du tableur sont‑ils en accord avec les résultats calculés dans les questions préliminaires ?
a. Remplir les cellules C5 à N5 pour obtenir une série aléatoire de douze 0 et 1. 0 indique que la bille va à gauche et 1 qu'elle va à droite.
b. Quelle formule doit‑on entrer dans la cellule B5 pour obtenir la valeur de la case d'arrivée de la bille ?
3. a. Simuler la chute de 1 000 billes.
b. Utiliser la ligne 2 pour compter le nombre de billes dans chacune des cases d'arrivée.
c. Les résultats obtenus à l'aide du tableur sont‑ils en accord avec les résultats calculés dans les questions préliminaires ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah