Physique-Chimie Terminale Spécialité

Rejoignez la communauté !

Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.

Préparation aux épreuves du Bac

1. Constitution et transformations de la matière

Composition et évolution d'un système

Ouverture de thème p. 16-17

Ch. 1

Modélisation des transformations acide-base

Ch. 2

Analyse physique d'un système chimique

Ch. 3

Méthode de suivi d'un titrage

Ch. 4

Évolution temporelle d'une transformation chimique

Ch. 5

Évolution temporelle d'une transformation nucléaire

BAC

Thème 1

Prévision et stratégie en chimie

Ouverture de thème p. 146-147

Ch. 6

Évolution spontanée d'un système chimique

Ch. 7

Équilibres acide-base

Ch. 8

Transformations chimiques forcées

Ch. 9

Structure et optimisation en chimie organique

Ch. 10

Stratégies de synthèse

BAC

Thème 1 bis

2. Mouvement et interactions

Ouverture de thème

p. 290-291

Ch. 11

Description d'un mouvement

Ch. 12

Mouvement dans un champ uniforme

Ch. 13

Mouvement dans un champ de gravitation

Ch. 14

Modélisation de l'écoulement d'un fluide

BAC

Thème 2

3. Conversions et transferts d'énergie

Ouverture de thème

p. 402-403

Ch. 15

Étude d’un système thermodynamique

Ch. 16

Bilans d'énergie thermique

BAC

Thème 3

4. Ondes et signaux

Ouverture de thème

p. 462-463

Ch. 17

Propagation des ondes

Ch. 18

Interférences et diffraction

Ch. 19

Lunette astronomique

Ch. 20

Effet photoélectrique et enjeux énergétiques

Ch. 21

Évolutions temporelles dans un circuit capacitif

BAC

Thème 4

Annexes

Ch. 22

Méthode

Chapitre 18

Activité 5 - Activité expérimentale

120 min

Étoiles et diffraction

Ce document est actuellement projeté sur le côté de votre écran.

Objectif : Exploiter la relation liant angle caractéristique de diffraction, longueur d'onde et taille de l'ouverture.

Ce document est actuellement projeté sur le côté de votre écran.

Problématique de l'activité

Lorsque l'on regarde certaines photographies astronomiques, on peut s'étonner de constater que les astres possèdent des « branches » leur donnant l'aspect... d'une étoile !

Pourquoi les astres observés au télescope ont-ils une forme en étoile ?

Ce document est actuellement projeté sur le côté de votre écran.

Doc. 1
Photographies de Sirius

Ci-dessous, deux photographies de l'étoile Sirius prises avec deux télescopes différents. Sur la photographie de gauche, Sirius comporte quatre branches alors qu'elle en compte six sur celle de droite.

Le zoom est accessible dans la version Premium.

Crédits : Tragoolchitr Jittasaiyapan/Shutterstock, Sanford John/SPL

Ce document est actuellement projeté sur le côté de votre écran.

Doc. 2
Araignée d'un télescope

Certains télescopes sont constitués d'un miroir secondaire situé à l'entrée du télescope qui permet l'observation des objets célestes à travers l'oculaire après réflexion de la lumière incidente sur le miroir primaire. Ce miroir secondaire est maintenu par des « bras » appelés aigrettes. L'ensemble

{

aigrettes

+

miroir

}

constitue ce que l'on appelle une araignée.

Le zoom est accessible dans la version Premium.

Crédits : lelivrescolaire.fr

Le nombre de bras de l'araignée d'un télescope peut varier d'un modèle à l'autre. Les images ci-dessous montrent les trois types d'araignée les plus rencontrés.

Le zoom est accessible dans la version Premium.

Crédits : lelivrescolaire.fr

Ce document est actuellement projeté sur le côté de votre écran.

Doc. 3
Diffraction de la lumière par une fente

Une fente diffracte la lumière qui la traverse. Si la fente est suffisamment petite, la figure de diffraction, observée dans un plan parallèle à la fente, est constituée d'une série de taches réparties sur un axe perpendiculaire à la direction de la fente. Ainsi, une fente verticale donne une figure de diffraction s'étalant sur un axe horizontal. Par ailleurs, la largeur

L

de la tache centrale est deux fois plus grande que celle des autres. L'écart angulaire

θ

peut être calculé à partir de la relation :

θ = \frac{λ}{a}

θ

: écart angulaire (rad)

λ

: longueur d'onde (m)

a

: largeur de la fente (m)

$Diffraction de la lumière par une fente$

Le zoom est accessible dans la version Premium.

Crédits : lelivrescolaire.fr

$Diffraction de la lumière par une fente$

Le zoom est accessible dans la version Premium.

Crédits : lelivrescolaire.fr

Ce document est actuellement projeté sur le côté de votre écran.

Doc. 4
Théorème de Babinet

Le théorème de Babinet énonce que deux objets de forme complémentaire produisent des figures de diffraction identiques. Ceci s'explique par le fait que le phénomène de diffraction est produit par les bords de l'objet diffractant. Ainsi, un fil ou une fente de même largeur produisent des figures de diffraction identiques.

Le zoom est accessible dans la version Premium.

Crédits : lelivrescolaire.fr

► Deux objets diffractants produisant la même figure.

Ce document est actuellement projeté sur le côté de votre écran.

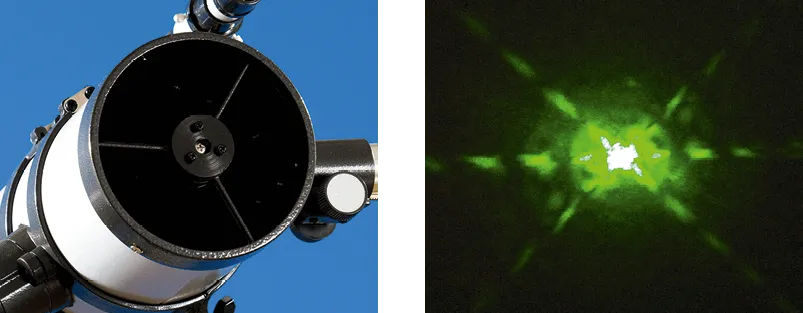
Doc. 5
Image d'une étoile

Les deux photographies ci-dessous montrent une reproduction de l'araignée à trois bras d'un télescope (à gauche) et la figure de diffraction obtenue (à droite).

Le zoom est accessible dans la version Premium.

Crédits : Science Photo Library/Alamy, Vincent Aimé

Ce document est actuellement projeté sur le côté de votre écran.

Doc. 6
Matériel nécessaire

Source lumineuse laser
Fente calibrée
Jeu de fils calibrés
Diapositives avec une araignée et supports

Écran avec support
Mètre ruban
Logiciel tableur-grapheur

Ce document est actuellement projeté sur le côté de votre écran.

Doc. 7
Incertitude

L'incertitude

u (x)

obtenue pour la mesure d'une grandeur

x

à l'aide d'un instrument de mesure de plus petite graduation

r

est égale à :

u (x) = \frac{r}{2 3}

Ce document est actuellement projeté sur le côté de votre écran.

Questions

APP : Extraire l'information utile
REA : Mettre en œuvre un protocole
VAL : Analyser des résultats
REA : Respecter les règles de sécurité

Compétence(s)

1. Préciser si la tache centrale de diffraction due à une même fente est plus large pour une distance fente‑écran

D

égale à

1, 00

1, 30

1, 50

m ou

1, 80

m. En déduire le choix de distance le plus judicieux.

2. Réaliser le montage permettant d'observer la figure de diffraction par une fente calibrée puis un fil calibré de même épaisseur

a = 40

µm. Vérifier que les figures obtenues sont bien en accord avec les informations fournies dans le et le .

3. Mesurer simplement la largeur de la tache centrale de diffraction et noter la valeur

L_{1}

obtenue. Calculer l'incertitude-type

u (L_{1})

sur la mesure de

L_{1}

puis écrire le résultat sous la forme

L_{1} \pm u (L_{1})

4. Proposer une méthode pour augmenter la précision de la mesure, puis la mettre en œuvre et calculer la nouvelle incertitude-type sur la mesure de

L_{2}

avec cette méthode. Écrire le résultat sous la forme

L_{2} \pm u (L_{2})

5. Confirmer que la précision a bien été augmentée en comparant les incertitudes relatives.

6. Lorsque

θ

est petit, on considère que

tan (θ) \approx θ

. Dans le , le triangle

FOM

est rectangle en

O

, déterminer l'expression de l'écart angulaire

θ

en fonction de

D

L

7. En déduire une expression de

L

en fonction de

a

D

λ

8. Réaliser plusieurs mesures avec différentes valeurs de

a

. Puis, en utilisant un tableur-grapheur, tracer le graphe représentant l'évolution de

L

en fonction de

\frac{1}{a}

. Modéliser la courbe obtenue.

Dessinez ici

9. Déduire de l'expression trouvée à la question 7. et du graphe tracé, la valeur de la longueur d'onde

λ

du laser. Calculer l'incertitude type

u (λ)

en considérant que les seules sources d'incertitudes à considérer sont sur les mesures de

L

et de

D

et présenter le résultat sous la forme

λ \pm u (λ)

\frac{u ( λ )}{λ} = (\frac{u ( D )}{D})^{2} + (\frac{u ( L )}{L})^{2}

10. Justifier la forme de la figure de diffraction obtenue avec une araignée à trois branches.

11. Reproduire soigneusement les araignées du puis dessiner la figure de diffraction obtenue dans chaque cas.

Dessinez ici

Ce document est actuellement projeté sur le côté de votre écran.

Synthèse de l'activité

Expliquer en quelques lignes la forme des étoiles observées à travers un télescope.

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

Oups, une coquille

j'ai une idée !

Nous préparons votre pageNous vous offrons 5 essais

Yolène

Émilie

Jean-Paul

Fatima

Sarah

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.