Physique-Chimie Terminale Spécialité
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Préparation aux épreuves du Bac
1. Constitution et transformations de la matière
Ch. 1
Modélisation des transformations acide-base
Ch. 2
Analyse physique d'un système chimique
Ch. 3
Méthode de suivi d'un titrage
Ch. 4
Évolution temporelle d'une transformation chimique
Ch. 5
Évolution temporelle d'une transformation nucléaire
BAC
Thème 1
Ch. 6
Évolution spontanée d'un système chimique
Ch. 7
Équilibres acide-base
Ch. 8
Transformations chimiques forcées
Ch. 9
Structure et optimisation en chimie organique
Ch. 10
Stratégies de synthèse
BAC
Thème 1 bis
2. Mouvement et interactions
Ch. 11
Description d'un mouvement
Ch. 12
Mouvement dans un champ uniforme
Ch. 13
Mouvement dans un champ de gravitation
Ch. 14
Modélisation de l'écoulement d'un fluide
BAC
Thème 2
3. Conversions et transferts d'énergie
Ch. 15
Étude d’un système thermodynamique
Ch. 16
Bilans d'énergie thermique
BAC
Thème 3
4. Ondes et signaux
Ch. 17
Propagation des ondes
Ch. 18
Interférences et diffraction
Ch. 19
Lunette astronomique
Ch. 20
Effet photoélectrique et enjeux énergétiques
Ch. 21
Évolutions temporelles dans un circuit capacitif
BAC
Thème 4
Annexes
Ch. 22
Méthode
Chapitre 18
Exercices
Pour s'échauffer - Pour commencer
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
| Pour commencer | Différenciation | Pour s'entraîner | |
|---|---|---|---|
| Savoir caractériser les phénomènes d'interférences et de diffraction | |||
| Savoir établir les conditions d'interférences et de diffraction | |||
| Savoir exploiter les relations liées aux interférences à deux ondes | |||
| Savoir exploiter les relations liées à la diffraction |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour s'échauffer
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5Conditions d'interférences
Énoncer les conditions pour que deux ondes périodiques sinusoïdales produisent des interférences stables et observables.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6Interfrange
Deux fentes d'Young de largeur l = 0{,}050 mm, distantes de a = 0{,}50 mm et situées à une distance D = 1{,}80 m d'un écran, sont éclairées par une source laser de longueur d'onde \lambda = 550 nm.
Déterminer la valeur de l'interfrange i.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7Conditions de diffraction
Une onde rencontre un obstacle de petite dimension notée a.Préciser la ou les condition(s) pour que l'onde soit diffractée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8Diffraction des ondes sonores
Une onde sonore de longueur d'onde \lambda = 30 cm rencontre une ouverture de largeur a = 4{,}0 m.
Calculer, en (rad) puis en (°), l'angle caractéristique de diffraction \theta.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9Figures de diffraction
Préciser la forme géométrique d'une ouverture dont la figure de diffraction est donnée ci-dessous.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10Diffraction par une fente
Pour une fente fine de largeur quelconque, préciser en justifiant quelle est la radiation la plus diffractée entre une radiation monochromatique rouge ou bleue.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour commencer
Périodicité d'une onde
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
11Périodicité d'une onde
✔ REA/MATH : Utiliser des outils mathématiques
Une onde mécanique progressive sinusoïdale de fréquence f = 1{,}5 MHz et de phase à l'origine \varphi = \dfrac{\pi}{2} se propage avec la célérité c = 1 \: 500 m⋅s-1.
Déterminer la période T ainsi que la longueur \lambda de l'onde mécanique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
12Représentation schématique
✔ APP : Faire un schéma
Représenter sous forme d'un schéma la période spatiale et la période temporelle d'une onde mécanique progressive sinusoïdale.
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
13Identification d'une onde sinusoïdale
✔ REA/MATH : Utiliser des outils mathématiques
L'amplitude d'une onde mécanique est modélisée par la fonction suivante :
s(x, t)=2{,}0 \times \cos \left(\dfrac{2 \pi}{2{,}0 \times 10^{-3}} \times\left(t-\dfrac{x}{c}\right)+\dfrac{\pi}{3}\right) 1. À partir de l'expression ci-dessus, déterminer la valeur de la période T et de la phase à l'origine \varphi.
2. Déterminer la valeur de l'amplitude s de l'onde à l'origine (x et t sont nuls).
3. À x = 0 m, représenter graphiquement l'évolution de l'amplitude de l'onde s(x, t) sur une durée égale à 3\: T à la calculatrice.
4. Sur le même graphique, représenter une onde identique mais dont le déphasage à l'origine est égal à zéro.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Interférences d'ondes périodiques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
14Expérience d'Young
✔ VAL : Faire preuve d'esprit critique
Thomas Young élabore en 1801 un dispositif pour démontrer la nature ondulatoire de la lumière. Cette expérience est restée célèbre sous le nom d'expérience des trous d'Young. Vers 1818, le français Augustin Fresnel a l'idée de remplacer les trous par des fentes.
Parmi les trois photographies ci-dessous, identifier celles qui correspondent aux deux expériences décrites dans l'énoncé. Justifier.


a


b


c
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
15Interférence sonore
✔ APP : Faire un schéma
Une vidéo a créé le buzz en montrant un appareil capable d'annuler le bruit venant de l'extérieur d'un appartement en le ventousant simplement sur la fenêtre. Si cette technologie existe pour les casques audio à réduction active de bruit, qu'en est-il pour une pièce entière ?
1. Nommer le phénomène sur lequel repose le principe de fonctionnement des casques à réduction active de bruit.
2. Schématiser simplement le principe physique de fonctionnement d'un tel appareil.
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
16Interférences à la surface d'un liquide
✔ REA : Utiliser un modèle
Deux vibreurs \text{V}_1 et \text{V}_2 synchrones de fréquence 200 Hz produisent des ondes à la surface d'un liquide qui se propagent à la célérité c = 4{,}0 m⋅s-1. La distance qui les sépare est a = 16 cm.
1. Déterminer la longueur d'onde des ondes produites par chacun des deux vibreurs.
2. Un point \text{P} est situé sur l'axe reliant \text{V}_1 et \text{V}_2 à une distance b du vibreur \text{V}_1. Faire un schéma et exprimer la différence de chemin \delta = \text{V}_1\text{P} - \text{V}_2\text{P} au point \text{P} entre les deux ondes en fonction de a et b.
2. Un point \text{P} est situé sur l'axe reliant \text{V}_1 et \text{V}_2 à une distance b du vibreur \text{V}_1. Faire un schéma et exprimer la différence de chemin \delta = \text{V}_1\text{P} - \text{V}_2\text{P} au point \text{P} entre les deux ondes en fonction de a et b.
Cliquez pour accéder à une zone de dessin
3. Exprimer la relation entre la différence de chemin et la longueur d'onde \lambda pour des interférences constructives.
4. Préciser les valeurs de b pour lesquelles l'amplitude des ondes au point \text{P} est maximale.
5. Calculer le nombre de franges d'interférences d'amplitude maximale entre les deux vibreurs.
4. Préciser les valeurs de b pour lesquelles l'amplitude des ondes au point \text{P} est maximale.
5. Calculer le nombre de franges d'interférences d'amplitude maximale entre les deux vibreurs.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Diffraction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17Angle caractéristique de diffraction
✔ APP : Faire un schéma
On réalise la figure de diffraction d'un fil calibré d'épaisseur 60 \: \mum avec un laser de longueur d'onde dans le vide \lambda = 550 nm.
1. Déterminer la couleur du laser.
2. Faire un schéma de la situation en faisant apparaître \theta, l'angle caractéristique de diffraction.
Cliquez pour accéder à une zone de dessin
3. Calculer la valeur de \theta.
4. La largeur de la tache centrale de diffraction est de 2{,}0 cm. Déterminer la distance D à laquelle se situe le fil calibré de l'écran.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
18Restitution d'un son
✔ REA : Utiliser un modèle
Une enceinte est constituée d'un caisson dans lequel est placé un haut-parleur. Le son sort de l'enceinte par une ouverture de diamètre d = 18 cm.
Une enceinte est constituée d'un caisson dans lequel est placé un haut-parleur. Le son sort de l'enceinte par une ouverture de diamètre d = 18 cm.
Données
1. Calculer les longueurs d'onde des ondes sonores de fréquence 200 Hz, 2{,}0 kHz et 20 kHz.
2. Préciser quel son sera le mieux diffracté à la sortie du haut-parleur.
2. Préciser quel son sera le mieux diffracté à la sortie du haut-parleur.
3. En justifiant, préciser si une personne placée sur le côté d'une enceinte entendra davantage les sons graves ou les sons aigus.
4. Les enceintes comportent au minimum deux hautparleurs : le woofer et le tweeter. Expliquer pourquoi les diamètres de ces haut-parleurs sont différents.
4. Les enceintes comportent au minimum deux hautparleurs : le woofer et le tweeter. Expliquer pourquoi les diamètres de ces haut-parleurs sont différents.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19Diffraction à la surface de l'eau
✔ VAL : Analyser des résultats
L'image ci-dessous est la photographie de la propagation d'ondes progressives périodiques à la surface de l'eau dans une cuve à ondes. Les ondes se propagent vers la droite.




1. Expliquer ce que cette expérience illustre.
2. Comparer les dimensions de l'ouverture de l'obstacle avec la longueur d'onde.
3. Préciser comment évolue la longueur avant et après le passage de l'onde par l'ouverture.
2. Comparer les dimensions de l'ouverture de l'obstacle avec la longueur d'onde.
3. Préciser comment évolue la longueur avant et après le passage de l'onde par l'ouverture.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Courbe d'intensité
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20Profil des franges d'interférences
✔ REA : Appliquer une formule
Une expérience d'interférences est réalisée avec deux fentes fines parallèles éclairées par un faisceau laser de longueur d'onde \lambda = 520 nm.
Le profil en intensité lumineuse récupéré par le capteur situé à 1{,}50 m des fentes est donné ci-après.
Une expérience d'interférences est réalisée avec deux fentes fines parallèles éclairées par un faisceau laser de longueur d'onde \lambda = 520 nm.
Le profil en intensité lumineuse récupéré par le capteur situé à 1{,}50 m des fentes est donné ci-après.

2. Calculer la valeur de l'écartement a entre les fentes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21Interférences versus diffraction
✔ RAI/ANA : Construire un raisonnement
Le profil en intensité d'une expérience d'interférences avec des fentes d'Young est fourni sur le doc. suivant. En regardant ce graphe, un élève pense qu'il s'agit d'un phénomène de diffraction. Il ajoute une courbe représentant l'enveloppe du profil en intensité.
Le profil en intensité d'une expérience d'interférences avec des fentes d'Young est fourni sur le doc. suivant. En regardant ce graphe, un élève pense qu'il s'agit d'un phénomène de diffraction. Il ajoute une courbe représentant l'enveloppe du profil en intensité.
Doc.
Profil en intensité

Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22Profil de la figure de diffraction
✔ APP : Extraire l'information utile
Une fente verticale de largeur a = 35 \: \mum est éclairée par un laser rouge. Le profil en intensité de la figure de diffraction est obtenu à une distance de 1{,}10 m de la fente.

1. Déterminer précisément la largeur L de la tache centrale de diffraction. En déduire la valeur de la longueur d'onde \lambda du laser.
2. Calculer la valeur de la largeur de la tache centrale de diffraction si un laser de longueur d'onde \lambda = 532 nm est utilisé.

1. Déterminer précisément la largeur L de la tache centrale de diffraction. En déduire la valeur de la longueur d'onde \lambda du laser.
2. Calculer la valeur de la largeur de la tache centrale de diffraction si un laser de longueur d'onde \lambda = 532 nm est utilisé.
3. Représenter l'allure du profil en intensité de la figure de diffraction obtenue avec ce laser.
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une notion, trois exercices
Différenciation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23
Longueur d'onde d'un laser
✔ REA : Appliquer une formule
Le dispositif des fentes d'Young est utilisé pour déterminer la longueur d'onde d'un laser.

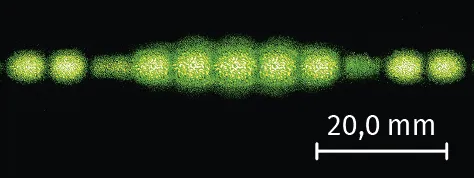
Une figure d'interférences est obtenue pour des fentes séparées d'une distance a = 0{,}20 mm. La distance entre les fentes et l'écran est D = 2{,}50 m.
1. Faire le schéma du dispositif des fentes d'Young.
Cliquez pour accéder à une zone de dessin
2. Donner la relation mathématique reliant l'interfrange i, la longueur d'onde \lambda du laser, les distances D et a.
3. En déduire une relation pour calculer la longueur d'onde \lambda du laser.
4. Déterminer la valeur de l'interfrange.
5. Calculer la longueur d'onde du laser. Vérifier sa cohérence avec l'image.
3. En déduire une relation pour calculer la longueur d'onde \lambda du laser.
4. Déterminer la valeur de l'interfrange.
5. Calculer la longueur d'onde du laser. Vérifier sa cohérence avec l'image.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24
Distance entre deux objets
✔ REA : Appliquer une formule
Le dispositif de Young peut également être utilisé pour déterminer la distance séparant deux fentes fines. Le dispositif est le même que celui de l'exercice précédent, la longueur d'onde du laser utilisé est \lambda = 600 nm et la distance entre les fentes et l'écran est de D = 2{,}50 m. La valeur trouvée pour dix interfranges est 3{,}3 cm.
1. Donner la relation mathématique permettant de déterminer la distance a séparant deux fentes fines en fonction de \lambda, D et i.
2. Déterminer la valeur de a.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25
Mesure de distance
✔ REA : Appliquer une formule
On réalise une figure d'interférences avec deux fentes séparées de a = 0{,}15 mm et un laser de longueur d'onde \lambda = 635 nm. L'interfrange mesurée est i = 1{,}83 mm.
Calculer la distance entre l'écran et les fentes.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
