Approfondissement

70

Environnement et développement durable

[Ch.1 - Mod.1 - Mod.8 - Cal.4.]

La géothermie, énergie renouvelable et non polluante, permet la production d'énergie électrique grâce à la chaleur des nappes d'eau souterraines. La centrale géothermique de Rittershoffen (Bas-Rhin) a été inaugurée le 7 juin 2016. On y a creusé un puits qui a la forme du tronc de cône représenté.


On calcule le volume d'un tronc de cône grâce à la formule suivante : $\mathrm{V}=\frac{\pi }{3}\times h\times \left({\mathrm{R}}^2+\mathrm{R}\times r+r^2\right)$, où $h$ désigne la hauteur du tronc de cône, $\text{R}$ le rayon de la grande base et $r$ le rayon de la petite base. Calculer le volume du puits en $m^3$.

Insérer une formule mathématique

71

[Ch.1 - Mod.1 - Mod.8 - Cal.4]

Ryan souhaite comparer la masse d'alcool de deux boissons. Il dispose des informations suivantes.



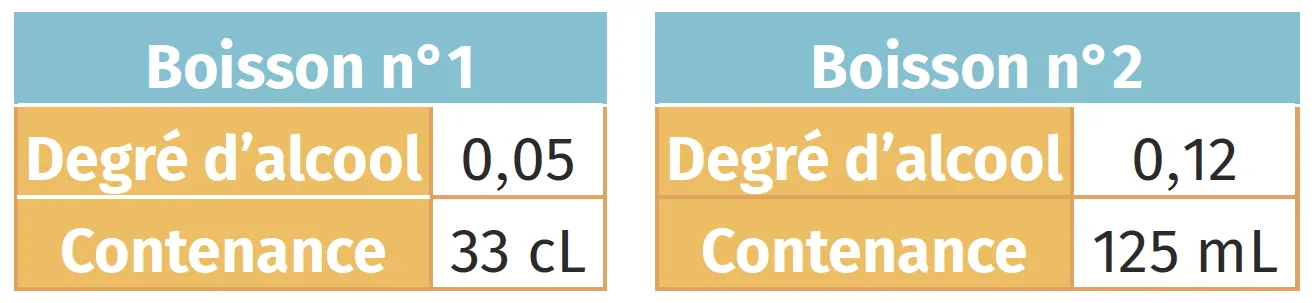
Quelle boisson a la masse d'alcool la plus élevée ? Justifier.

Insérer une formule mathématique

72

[Mod.8 - Rais.4 - Cal.4]

On considère le programme de calcul suivant.

$\boxed{\begin{array}{rl}1& \text{Choisir un nombre entier neˊgatif}\\ 2& \text{Le multiplier par 2}\\ 3& \text{Ajouter 3}\\ 4& \text{Multiplier le reˊsultat par –4}\\ 5& \text{Ajouter 4}\end{array}}$

1. Qu'obtient-on en choisissant $-3$ au départ ?

Insérer une formule mathématique

2. Soit $x$, le nombre de départ. Exprimer, en fonction de $x$, le résultat du programme.

Insérer une formule mathématique

3. Eva souhaite montrer que, quel que soit le nombre de départ, on obtient toujours un multiple de $8$.

a. Développer et réduire l'expression obtenue à la question 2. .

Insérer une formule mathématique

b. À l'aide d'une factorisation, démontrer que l'on obtient toujours un multiple de $8$.

Insérer une formule mathématique

73

[Ch.2 - Mod.8 - Rais.5 - Cal.4]

Paul construit une suite de maisons avec des allumettes comme représenté ci-après.



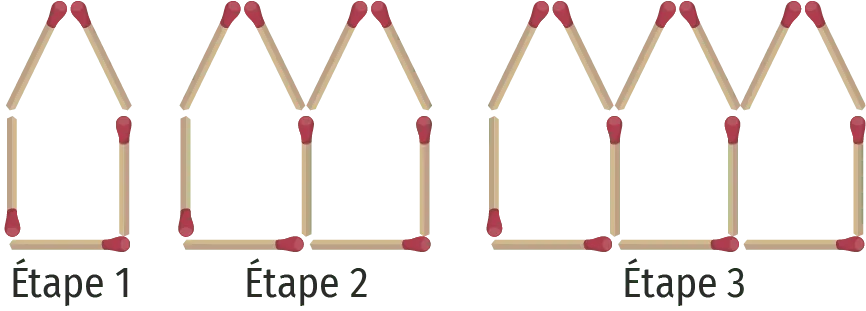
1. Combien d'allumettes faut-il pour construire quatre maisons (étape 4) ?

Insérer une formule mathématique

2. Soit $n$, le numéro de l'étape. Proposer une expression qui donne le nombre d'allumettes, en fonction de $n$, nécessaires à la construction de l'étape $n$.

Insérer une formule mathématique

3. Combien faut-il d'allumettes pour construire cette suite de maisons à l'étape 2020 ?

Insérer une formule mathématique

74

[Mod.8 - Rais.4 - Cal.4]

On considère le programme de calcul suivant.

$\boxed{\begin{array}{rl}1& \text{Choisir un nombre entier}\\ 2& \text{Le multiplier par 3}\\ 3& \text{Soustraire 6}\\ 4& \text{Eˊlever le reˊsultat au carreˊ}\end{array}}$

1. Qu'obtient-on en choisissant $-2$ au départ ?

Insérer une formule mathématique

2. Soit $x$, le nombre de départ. Exprimer, en fonction de $x$, le résultat du programme.

Insérer une formule mathématique

3. Démontrer que, quel que soit le nombre de départ, on obtient toujours un multiple de $9$.

Insérer une formule mathématique

75

[Mod.8 - Cal.4]

On considère l'expression $\mathrm{C}=(2x-3)(-x+1)+3$.

1. Développer et réduire $\text{C}$.

Insérer une formule mathématique

2. Factoriser $\text{C}$ à partir du résultat de la question 1. .

Insérer une formule mathématique

3. En utilisant la forme la plus adaptée, calculer $\text{C}$ pour :

a. $x=0$

Insérer une formule mathématique

b. $x=\frac{3}{2}$

Insérer une formule mathématique

c. $x=\frac{5}{2}$

Insérer une formule mathématique

76

Énigme

Un magicien affirme qu'il peut deviner l'âge des spectateurs. Pour cela, il fait monter une personne sur la scène puis il lui demande de réaliser en silence les calculs suivants :
« Ajoutez 3 à votre âge, multipliez par 10, divisez ensuite par 5 puis retranchez 5.»
Enfin, le magicien demande d'annoncer le nombre ainsi obtenu. Emma, la première volontaire à se prêter à ce tour de magie, annonce : « 47 ». Le magicien lui annonce immédiatement : « Tu as 23 ans ! ». Emma approuve.
Expliquer comment le magicien peut trouver l'âge du spectateur très rapidement une fois le résultat du calcul connu.

Insérer une formule mathématique

79

Casse-tête

Mia a un certain nombre de bonbons, plus grand que $6$, que l'on note $n$, Sofia en a $15$ de plus que Mia et Élise en a $3$ de plus que Sofia. Dans la journée, Mia mange $5$ bonbons, Sofia en mange $6$ et Élise en mange $7$. À la fin de la journée, elles mettent ce qui leur reste en commun et se les partagent équitablement. Exprimer, en fonction de $n$, le nombre de bonbons que reçoit chacune des filles à la fin de la journée.

Insérer une formule mathématique

77

Casse-tête

Sarah choisit un nombre entier. À la somme des carrés des deux entiers qui lui succèdent, elle retranche la somme des carrés des deux entiers qui le précèdent. Sarah prétend pouvoir trouver rapidement le résultat.
Expliquer son raisonnement.

Insérer une formule mathématique

78

Défi

Pour calculer rapidement le carré d'un nombre compris entre $26$ et $100$, on suit les étapes suivantes :

• Étape 1 : soustraire $25$ au nombre, puis le multiplier par $100$ ;
• Étape 2 : reprendre le nombre de départ, le soustraire à $50$, puis élever le résultat au carré ;
• Étape 3 : ajouter les résultats des étapes 1 et 2.

1. Démontrer que ce programme de calcul permet bien de calculer le carré d'un nombre.

Insérer une formule mathématique

2. Calculer mentalement $38^2$.

Insérer une formule mathématique