Mathématiques Terminale Bac Pro
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Statistique et probabilités
Ch. 1
Statistiques à deux variables
Ch. 2
Probabilités
Partie 2 : Algèbre - Analyse
Ch. 3
Suites numériques
Ch. 4
Fonctions polynômes de degré 3
Ch. 5
Fonctions exponentielles et logarithme décimal
Ch. 6
Calculs commerciaux et financiers
Partie 3 : Géométrie
Ch. 7
Vecteurs
Ch. 8
Trigonométrie
Annexes
Révisions Genially
Consolidation
Poursuite d'études
Annexes
Programmation
Cahier d'algorithmique et de programmation
Chapitre 2
Avant de commencer
Probabilités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
L'objectif de ce chapitre est de modéliser
des situations aléatoires par des arbres de
probabilités pondérés afin de déterminer
des probabilités. Ces situations sont
liées à des domaines variés : économie,
industrie, domaine médical, développement
durable, changement climatique, etc.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.


Les machines à sous sont monnaie courante à Las Vegas.
Avoir la chance de gagner le jackpot est le rêve de tout
joueur. Peut-on prédire nos chances de gagner aux jeux
de hasard ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Rappels de première
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Probabilité d'un événement dans le cas d'une situation équiprobable
La probabilité d᾽un événement \text{A} est {\mathrm{P}(\mathrm{A})=\frac{\text { nombre d'issues favorables à } \mathrm{A}}{\text { nombre total d'issues }}}Événement contraire
L'événement contraire de \text{A} est noté \overline{\mathrm{A}} et on a \mathrm{P}(\overline{\mathrm{A}})=1-\mathrm{P}(\mathrm{A}).Intersection et union
L'intersection des événements \text{A} et \text{B} se note \mathrm{A \cap B}. Elle est réalisée lorsque \text{A} et \text{B} sont réalisés.L'union de deux événements se note \mathrm{A} \cup \mathrm{B}. Elle est réalisée si au moins un des deux événements est réalisé.
Les probabilités de l'union et de l'intersection sont liées par la relation : \mathrm{P}(\mathrm{A} \cup \mathrm{B})=\mathrm{P}(\mathrm{A})+\mathrm{P}(\mathrm{B})-\mathrm{P}(\mathrm{A} \cap \mathrm{B}).

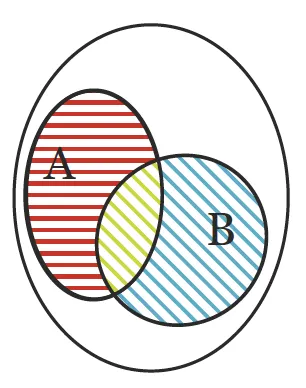
L'intersection correspond à la partie hachurée en vert du diagramme de Venn.
L'union correspond à toute la partie hachurée.
Probabilité conditionnelle
La probabilité que l'événement \text{B} se réalise sachant que l'événement \text{A} est réalisé se note \mathrm{P_{A}(B)} et est donnée par la relation \mathrm{P_{A}(B)=\frac{P(A \cap B)}{P(A)}}avec \mathrm{P}(\mathrm{A}) \neq 0.Tableau
Un tableau permet de classer les effectifs d'une population selon deux caractères différents. Dans le tableau ci-contre on a :\mathrm{P(A)=\frac{\color{purple}{40}}{\color{blue}{100}}=0,4} ; \mathrm{P}(\overline{\mathrm{A}} \cap \mathrm{B})=\frac{\color{orange}{10}}{\color{blue}{100}}=0,1 et \mathrm{P_{A}(B)=\frac{\color{green}20}{\color{purple}40}=0,5}.
| \text{A} | \overline{\mathrm{A}} | Total | |
| \text{B} | \color{green}20 | \color{orange}10 | 30 |
| \overline{\mathrm{B}} | 20 | 50 | 70 |
| Total | \color{purple}40 | 60 | \color{blue}100 |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Validation des acquis
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 1
Dans une urne, il y a trois boules blanches numérotées de 1 à 3 et six boules rouges numérotées de 4 à 9. On considère les événements suivants. \text{B} : « La boule piochée est
blanche », \text{R} : « La boule piochée est rouge » et
\text{A} : « La boule piochée porte un chiffre pair ».
On pioche une boule au hasard. Pour chaque probabilité, choisir la ou les bonne(s) réponse(s).
1. \text{P(R)=}
2. \mathrm{P}(\mathrm{R} \cap \mathrm{A})=
3. \mathrm{P}(\mathrm{B} \cup \mathrm{A})=
4. \mathrm{P_{A}(R)=}
5. \mathrm{P}(\overline{\mathrm{A}})=
1. \text{P(R)=}
2. \mathrm{P}(\mathrm{R} \cap \mathrm{A})=
3. \mathrm{P}(\mathrm{B} \cup \mathrm{A})=
4. \mathrm{P_{A}(R)=}
5. \mathrm{P}(\overline{\mathrm{A}})=
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 2
Voici les résultats d'une enquête portant
sur les jeux vidéo préférés des élèves d'un
lycée. On considère les événements suivants :
1. Compléter le tableau ci-dessous.
2. On choisit au hasard un élève.
a. Donner la probabilité qu'il s'agisse d'une fille qui préfère jouer à Minecraft.
b. Donner la probabilité que son jeu préféré soit Les Sims sachant que c'est une fille.
- \text{M} : « Le jeu préféré de l'élève est Minecraft » \text{S} : « Le jeu préféré de l'élève est Les Sims » ;
- \text{F} : « L'élève est une fille » et \text{G} : « L'élève est un garçon ».
1. Compléter le tableau ci-dessous.
| Minecraft | Les Sims | Total | |
| Fille | 31 | 99 | |
| Garçon | 7 | ||
| Total | 135 |
2. On choisit au hasard un élève.
a. Donner la probabilité qu'il s'agisse d'une fille qui préfère jouer à Minecraft.
b. Donner la probabilité que son jeu préféré soit Les Sims sachant que c'est une fille.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
