Mathématiques Terminale Bac Pro
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Statistique et probabilités
Ch. 1
Statistiques à deux variables
Ch. 2
Probabilités
Partie 2 : Algèbre - Analyse
Ch. 3
Suites numériques
Ch. 4
Fonctions polynômes de degré 3
Ch. 5
Fonctions exponentielles et logarithme décimal
Ch. 6
Calculs commerciaux et financiers
Partie 3 : Géométrie
Ch. 7
Vecteurs
Ch. 8
Trigonométrie
Annexes
Révisions Genially
Consolidation
Poursuite d'études
Annexes
Programmation
Cahier d'algorithmique et de programmation
Chapitre 2
Exercices
Probabilités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exploiter la lecture d'un arbre de probabilités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 1
Une étude a été réalisée sur l'ensemble de la
production de vélos dans deux entreprises A et B.
On sait que deux tiers des vélos proviennent de
l'entreprise A. Parmi les vélos de l'entreprise A,
40 % sont des vélos électriques alors qu'il n'y a
que 15 % de vélos électriques dans l'entreprise B.
On choisit au hasard un vélo dans l'ensemble de la
production. On note les événements \mathrm A : « Le vélo
provient de l'entreprise A », \mathrm B : « Le vélo provient de l'entreprise B » et \mathrm E : « Le vélo est électrique ».
L'arbre de probabilités pondéré ci‑après résume cette étude.
1. Compléter l'arbre de probabilités pondéré à l'aide de l'énoncé.
2. Donner la probabilité que le vélo provienne de l'entreprise B.
3. Interpréter les événements \mathrm {\overline{E}}, \mathrm{A \cap E} et \mathrm{B \cap \overline{E}}.
4. Donner la probabilité que le vélo choisi soit électrique sachant qu'il vient de l'entreprise A.
5. Donner la probabilité que le vélo choisi ne soit pas électrique sachant qu'il vient de l'entreprise B.
L'arbre de probabilités pondéré ci‑après résume cette étude.
1. Compléter l'arbre de probabilités pondéré à l'aide de l'énoncé.
2. Donner la probabilité que le vélo provienne de l'entreprise B.
3. Interpréter les événements \mathrm {\overline{E}}, \mathrm{A \cap E} et \mathrm{B \cap \overline{E}}.
4. Donner la probabilité que le vélo choisi soit électrique sachant qu'il vient de l'entreprise A.
5. Donner la probabilité que le vélo choisi ne soit pas électrique sachant qu'il vient de l'entreprise B.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 2
Copie d᾽élève
En devoir, un professeur a donné à ses élèves l'arbre
de probabilités pondéré suivant puis leur a demandé de
compléter le tableau correspondant.

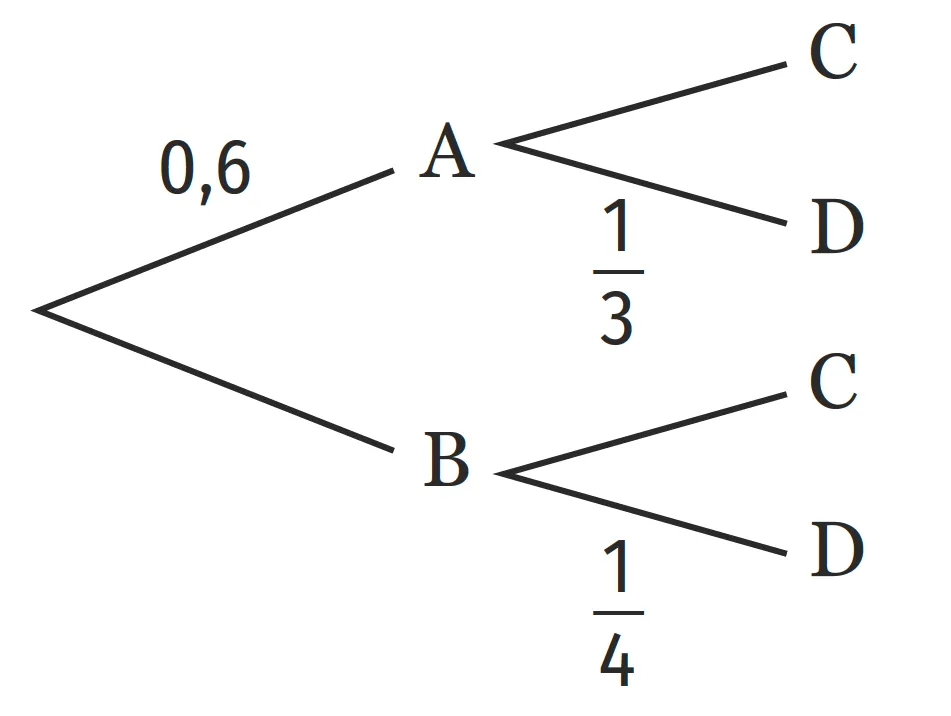
Les données du professeur sont en noir. Éloïse a écrit ses réponses en rouge. Indiquer les erreurs faites par Éloïse et corriger le tableau.


Les données du professeur sont en noir. Éloïse a écrit ses réponses en rouge. Indiquer les erreurs faites par Éloïse et corriger le tableau.
| A | B | Total | |
| C | 48 | 12 | 66 |
| D | 18 | 36 | 54 |
| Total | 72 | 48 | 120 |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 3
Modéliser chacune des situations aléatoires
suivantes par un arbre de probabilités.
1. On lance deux fois de suite une pièce de monnaie équilibrée, on note les événements \mathrm P : « La pièce tombe sur pile » et \mathrm F : « La pièce tombe sur face ».
2. On lance trois fois de suite un dé à six faces non truqué, on note l'événement \mathrm A : « On obtient un 1 ».
1. On lance deux fois de suite une pièce de monnaie équilibrée, on note les événements \mathrm P : « La pièce tombe sur pile » et \mathrm F : « La pièce tombe sur face ».
Cliquez pour accéder à une zone de dessin
2. On lance trois fois de suite un dé à six faces non truqué, on note l'événement \mathrm A : « On obtient un 1 ».
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 4
Inversé
Proposer une situation correspondant
à l'arbre de probabilités pondéré ci-après.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Calculer une probabilité
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 5
Copie d᾽élève
L᾽arbre de probabilités pondéré ci-après a
été réalisé par François puis validé par le professeur.

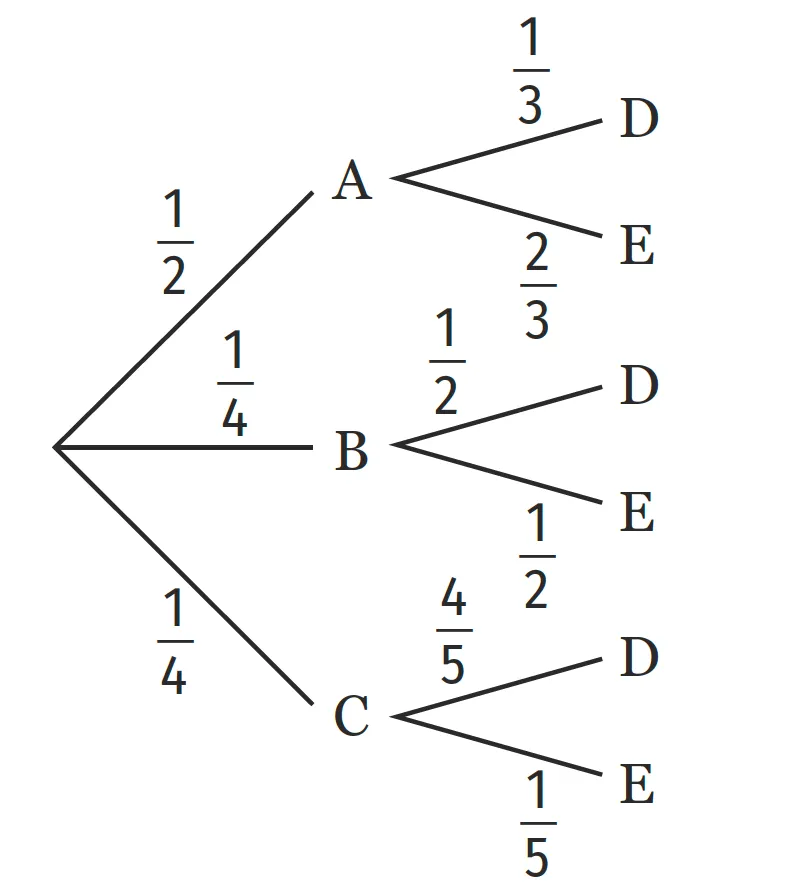
À la question « Déterminer la probabilité \mathrm{P(E)}» François propose la réponse suivante :
\mathrm{P(E)}=\frac{1}{2}+\frac{2}{3}+\frac{1}{4}+\frac{1}{2}+\frac{1}{4}+\frac{1}{5}=\frac{71}{30}=2,37
1. Sans calcul, indiquer pourquoi on peut savoir que le résultat donné par François est faux.
2. Déterminer la probabilité \mathrm {P(E)}.


À la question « Déterminer la probabilité \mathrm{P(E)}» François propose la réponse suivante :
\mathrm{P(E)}=\frac{1}{2}+\frac{2}{3}+\frac{1}{4}+\frac{1}{2}+\frac{1}{4}+\frac{1}{5}=\frac{71}{30}=2,37
1. Sans calcul, indiquer pourquoi on peut savoir que le résultat donné par François est faux.
2. Déterminer la probabilité \mathrm {P(E)}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 6
Un sac contient sept pièces de monnaie dont
trois pièces truquées. Une pièce truquée permet
d'obtenir face sept fois sur dix. Julian pioche une
pièce au hasard dans ce sac et la lance.
Donner la probabilité qu'il obtienne face.
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 7
Algorithmique
On lance deux fois de suite une pièce de monnaie
équilibrée et on s'intéresse au nombre de pile et
de face obtenus. On modélise cette situation par
l'algorithme ci-après.
1. Compléter les lignes 7 et 9 de ce programme afin qu'il donne en sortie le nombre de fois où la pièce est tombée sur pile et le nombre de fois où elle est tombée sur face.
2. Au lieu de lancer cette pièce de monnaie deux fois de suite, on souhaite la lancer dix fois. Comment doit-on modifier le programme pour simuler cette situation ?
3. On souhaite désormais simuler dix lancers d'une pièce de monnaie truquée, ayant 70 % de chance de tomber sur pile. Comment doit-on modifier le programme pour simuler cette situation ?
from random import * def lancer(): p = 0 f = 0 for k in range(2): if random() < 0.5: p = ... else: f = ... return(p, f) print(lancer())
1. Compléter les lignes 7 et 9 de ce programme afin qu'il donne en sortie le nombre de fois où la pièce est tombée sur pile et le nombre de fois où elle est tombée sur face.
2. Au lieu de lancer cette pièce de monnaie deux fois de suite, on souhaite la lancer dix fois. Comment doit-on modifier le programme pour simuler cette situation ?
3. On souhaite désormais simuler dix lancers d'une pièce de monnaie truquée, ayant 70 % de chance de tomber sur pile. Comment doit-on modifier le programme pour simuler cette situation ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 8
| Kobe Bryant | |
|---|---|
Palmarès :
|
  |
L'adresse aux lancers francs de Kobe Bryant était impressionnante.
- Il marquait 90 % de ses premiers lancers.
- S'il marquait le premier lancer, il marquait le second 85 % du temps.
- S'il échouait au premier lancer, il réussissait six fois sur dix le lancer suivant.
1. Dresser l'arbre de probabilités pondéré qui représente cette situation.
Cliquez pour accéder à une zone de dessin
L'équipe de Kobe Bryant perd d'un point. Il ne reste plus de temps au compteur mais une faute sur Kobe Bryant lui permet d'obtenir deux lancers francs à la fin du match. Au basket, un lancer franc réussi rapporte 1 point.
2. Déterminer la probabilité que l'équipe de Kobe Bryant gagne.
3. Déterminer la probabilité qu'il y ait une prolongation (égalité à la fin de la partie).
4. Déterminer la probabilité qu'il rate son second lancer franc.
5. Déterminer la probabilité qu'il ait réussi son premier lancer franc sachant qu'il a raté le second.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Indépendance
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 9
Indiquer, dans chacun des cas suivants, si les
événements \mathrm A et \mathrm B sont indépendants.
1. \mathrm{P}(\mathrm{A})=\frac{1}{4} ; \mathrm{P}(\mathrm{B})=0,25 \text { et } \mathrm{P}(\mathrm{A} \cap \mathrm{B})=\frac{1}{16}.
2. \mathrm{P}(\mathrm{A})=0{,}9 ; \mathrm{P}(\mathrm{B})=0{,}8 \text { et } \mathrm{P}(\mathrm{A} \cap \mathrm{B})=0{,}75.
3. \mathrm{P}(\mathrm{A})=0{,}7 ; \mathrm{P}(\overline{\mathrm{B}})=0{,}8 \text { et } \mathrm{P}(\mathrm{A} \cap \mathrm{B})=0{,}14.
1. \mathrm{P}(\mathrm{A})=\frac{1}{4} ; \mathrm{P}(\mathrm{B})=0,25 \text { et } \mathrm{P}(\mathrm{A} \cap \mathrm{B})=\frac{1}{16}.
2. \mathrm{P}(\mathrm{A})=0{,}9 ; \mathrm{P}(\mathrm{B})=0{,}8 \text { et } \mathrm{P}(\mathrm{A} \cap \mathrm{B})=0{,}75.
3. \mathrm{P}(\mathrm{A})=0{,}7 ; \mathrm{P}(\overline{\mathrm{B}})=0{,}8 \text { et } \mathrm{P}(\mathrm{A} \cap \mathrm{B})=0{,}14.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 10
Dans une urne opaque, il y a quinze boules
indiscernables au toucher, numérotées de 1 à 15.
Cinq d'entre elles sont rouges. On en tire une au
hasard et on considère les événements :
1. Déterminer les probabilités \mathrm{P(A)}, \mathrm{P(B)} et \mathrm{P(C)}.
2. À quoi correspond l'événement \mathrm{A \cap B} ?
3. Peut-on calculer \mathrm{P(A \cap B)} ? Pourquoi ?
4. À quoi correspond l'événement \mathrm{B \cap C} ?
5. Calculer la probabilité \mathrm{P(B \cap C)}.
6. Les événements \mathrm B et \mathrm C sont-ils indépendants ?
- \mathrm A : « La boule est rouge » ;
- \mathrm B : « Le chiffre est inférieur ou égal à cinq » ;
- \mathrm C : « Le chiffre est un multiple de cinq ».
1. Déterminer les probabilités \mathrm{P(A)}, \mathrm{P(B)} et \mathrm{P(C)}.
2. À quoi correspond l'événement \mathrm{A \cap B} ?
3. Peut-on calculer \mathrm{P(A \cap B)} ? Pourquoi ?
4. À quoi correspond l'événement \mathrm{B \cap C} ?
5. Calculer la probabilité \mathrm{P(B \cap C)}.
6. Les événements \mathrm B et \mathrm C sont-ils indépendants ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Bilan
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 11
Une machine à sous, comme montré en page d᾽introduction du chapitre, est composée de trois cylindres identiques. Elle affiche aléatoirement un
symbole sur chaque cylindre.
Chaque cylindre comporte dix symboles : deux fois le symbole « 7 » ; trois fois le symbole « BAR » et cinq fois le symbole « X ».
Aligner trois « 7 » rapporte 35 $, aligner trois « BAR » rapporte 15 $ et aligner trois « X » rapporte 10 $. Une partie coûte 2 $.
Une telle machine est-elle rentable pour le casino ?
1. Déterminer la probabilité d'avoir trois « 7 », puis celle d'avoir trois « BAR » et enfin celle d'avoir trois « X ».
2. Déterminer la probabilité de perdre sachant que l'on perd si on n'aligne pas trois symboles identiques.
3. Calculer le produit de la probabilité d'avoir trois « 7 » par le gain correspondant. Faire de même pour les autres situations.
4. Additionner les quatre résultats de la question précédente afin de déterminer le gain moyen.
5. Répondre à la question posée dans l᾽énoncé.
Chaque cylindre comporte dix symboles : deux fois le symbole « 7 » ; trois fois le symbole « BAR » et cinq fois le symbole « X ».
Aligner trois « 7 » rapporte 35 $, aligner trois « BAR » rapporte 15 $ et aligner trois « X » rapporte 10 $. Une partie coûte 2 $.
Une telle machine est-elle rentable pour le casino ?
1. Déterminer la probabilité d'avoir trois « 7 », puis celle d'avoir trois « BAR » et enfin celle d'avoir trois « X ».
2. Déterminer la probabilité de perdre sachant que l'on perd si on n'aligne pas trois symboles identiques.
3. Calculer le produit de la probabilité d'avoir trois « 7 » par le gain correspondant. Faire de même pour les autres situations.
4. Additionner les quatre résultats de la question précédente afin de déterminer le gain moyen.
5. Répondre à la question posée dans l᾽énoncé.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 12
Algorithmique
En reprenant les données de l'exercice précédent, un professeur de mathématiques a simulé une partie avec cette machine à sous. Un cylindre simplifié de la machine est présenté ci-après.

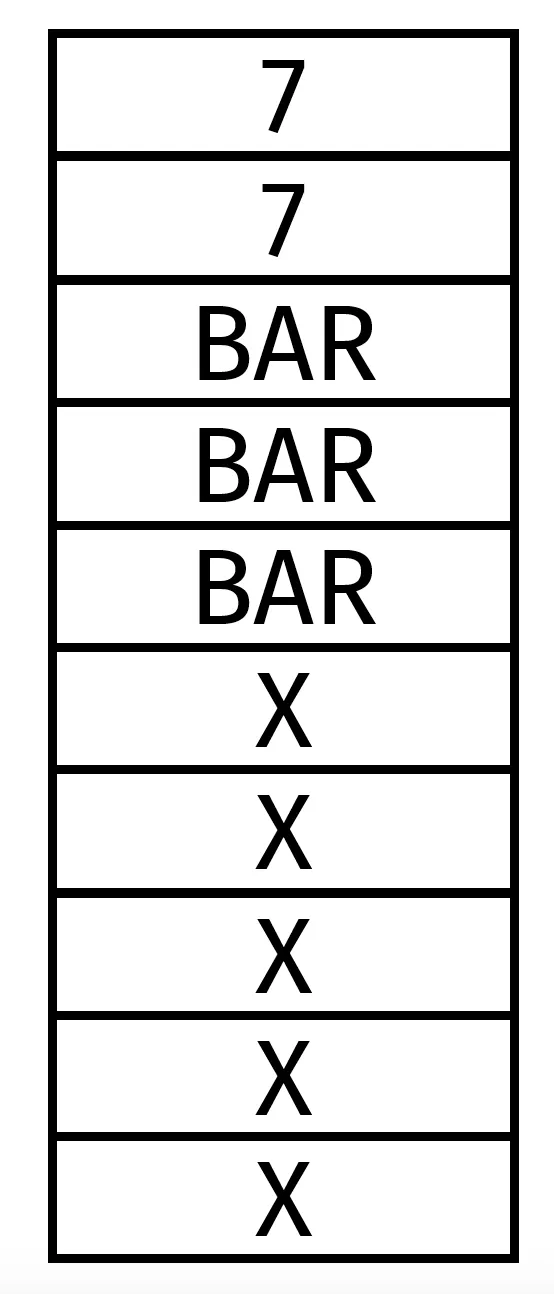
1. Compléter le programme puis simuler plusieurs parties.
En mathématiques, on appelle espérance la valeur qu'on s'attend à trouver en moyenne si on répète un grand nombre de fois une simulation.
2. Quelle est l'espérance de ce jeu ?
3. Le résultat est-il en accord avec celui de l'exercice précédent ?
4. Interpréter cette phrase : « Les jeux de casino sont dits à espérance négative ».


1. Compléter le programme puis simuler plusieurs parties.
En mathématiques, on appelle espérance la valeur qu'on s'attend à trouver en moyenne si on répète un grand nombre de fois une simulation.
2. Quelle est l'espérance de ce jeu ?
3. Le résultat est-il en accord avec celui de l'exercice précédent ?
4. Interpréter cette phrase : « Les jeux de casino sont dits à espérance négative ».
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 13
Le tableau ci-après recense les machines de sport
utilisées par les adhérents
d'un club de fitness.
On choisit au hasard un des adhérents du club. On considère les événements \mathrm A : « La personne est une femme », \mathrm B : « La personne utilise le tapis de course » et \mathrm C : « La personne utilise le rameur ».
1. Déterminer les probabilités \mathrm {P(A)} et \mathrm {P(B)}.
2. Montrer que les événements \mathrm {A} et \mathrm {B} sont indépendants.
3. Les événements \mathrm {A} et \mathrm {C} sont-ils indépendants ?
| Homme | Femme | Total | |
|---|---|---|---|
| Tapis de course | 7 | 14 | 21 |
| Vélo elliptique | 2 | 19 | 21 |
| Rameur | 15 | 15 | 30 |
| Total | 24 | 48 | 72 |
On choisit au hasard un des adhérents du club. On considère les événements \mathrm A : « La personne est une femme », \mathrm B : « La personne utilise le tapis de course » et \mathrm C : « La personne utilise le rameur ».
1. Déterminer les probabilités \mathrm {P(A)} et \mathrm {P(B)}.
2. Montrer que les événements \mathrm {A} et \mathrm {B} sont indépendants.
3. Les événements \mathrm {A} et \mathrm {C} sont-ils indépendants ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 14
La vie scolaire d'un établissement réalise une
étude sur les liens entre les retards des bus (donc
des élèves) et les conditions météorologiques.
Voici le relevé portant sur un total de 400 bus.
On choisit au hasard un de ces bus. On considère les événements \mathrm P : « Il pleut » et \mathrm R : « Le bus est en retard ». Les événements \mathrm P et \mathrm R sont-ils indépendants ? Justifier puis interpréter la réponse.


| Beau temps | Pluie | |
|---|---|---|
| Bus en retard | 30 | 15 |
| Bus à l'heure | 335 | 20 |
On choisit au hasard un de ces bus. On considère les événements \mathrm P : « Il pleut » et \mathrm R : « Le bus est en retard ». Les événements \mathrm P et \mathrm R sont-ils indépendants ? Justifier puis interpréter la réponse.


Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
