Mathématiques 3e - 2021
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Nombres et calculs
Ch. 1
Nombres entiers
Ch. 2
Calcul numérique
Ch. 3
Calcul littéral
Ch. 4
Équations
Partie 2 : Organisation et gestion de données, fonctions
Ch. 5
Notion de fonction
Ch. 6
Fonctions affines
Ch. 7
Situations de proportionnalité
Ch. 8
Statistiques
Ch. 9
Probabilités
Partie 3 : Espace et géométrie
Ch. 10
Théorème de Thalès et triangles semblables
Ch. 11
Trigonométrie dans le triangle rectangle
Ch. 12
Transformations dans le plan et leurs effets
Ch. 13
Géométrie dans l'espace
Partie 4 : Mesures et grandeurs
Ch. 14
Mesures et grandeurs
Annexes
Scratch
Dossier brevet
Rappels, Index, Compétences
Révisions Genially
Calcul littéral
Plan de travail
Chapitre 5
Révisions
Notion de fonction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.

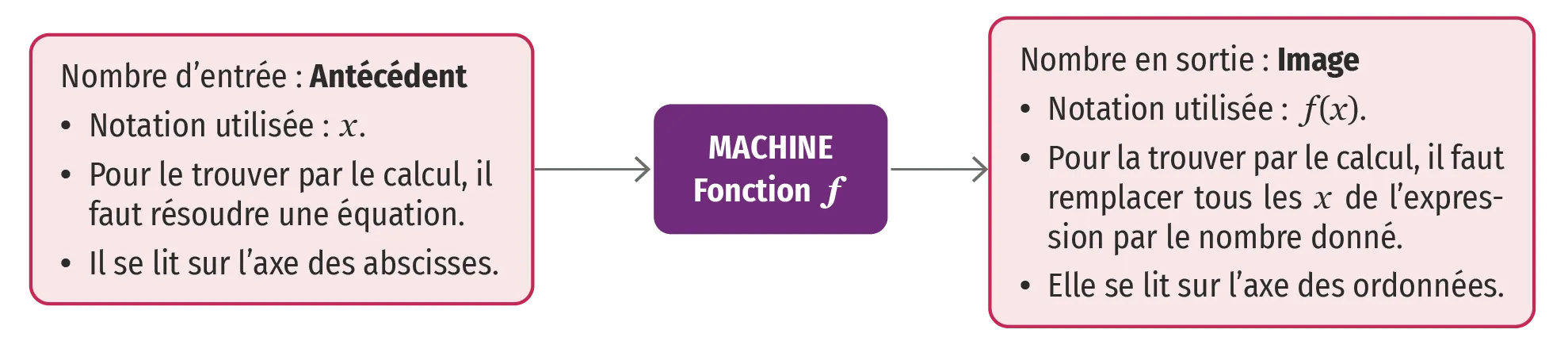
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
QCU : réponse unique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6
On donne f : 2 \mapsto -8 et f(4) = -6. Quelle affirmation est vraie ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7
Soit g la fonction définie par g : x \mapsto x^2 - 9. L'image de -3 par g est :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8
On donne ci‑dessous le tableau de valeurs d'une fonction h.
| \boldsymbol{x} | -2 | -1 | 0 | 1 |
| \boldsymbol{h(x)} | 3 | -0{,}5 | -1{,}5 | -2 |
Quelle affirmation est vraie ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9
Soit j la fonction définie par j(x) = 2x - 3. Un antécédent de 0 par j est :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
QCM : réponses multiples
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10
On donne ci‑dessous la courbe représentative d'une fonction k.Quelles affirmations sont vraies ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
11
On donne ci‑dessous la courbe représentative d'une fonction \ell.Quelles affirmations sont vraies ?

Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
