Découvrir le chapitre : trigonométrie dans le triangle rectangle

Partie A : Papier et crayon

1

Tracer un triangle \text{ABC} rectangle en \text{B} tel que \widehat{\text{BAC}} = 30°.

GeoGebra

Accéder au module

Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail

2

Quelle est l'hypoténuse de ce triangle ? Quel est le côté adjacent à l'angle \widehat{\text { BAC }} ? Quel est le côté opposé à cet angle ?

3

Mesurer la longueur des trois côtés de ce triangle puis calculer les quotients : \frac{\mathrm{AB}}{\mathrm{AC}}, \frac{\mathrm{BC}}{\mathrm{AC}} et \frac{\mathrm{BC}}{\mathrm{AB}}.

4

Comparer les valeurs des quotients obtenues par tous les élèves de la classe.

Partie B : Avec un logiciel de géométrie dynamique

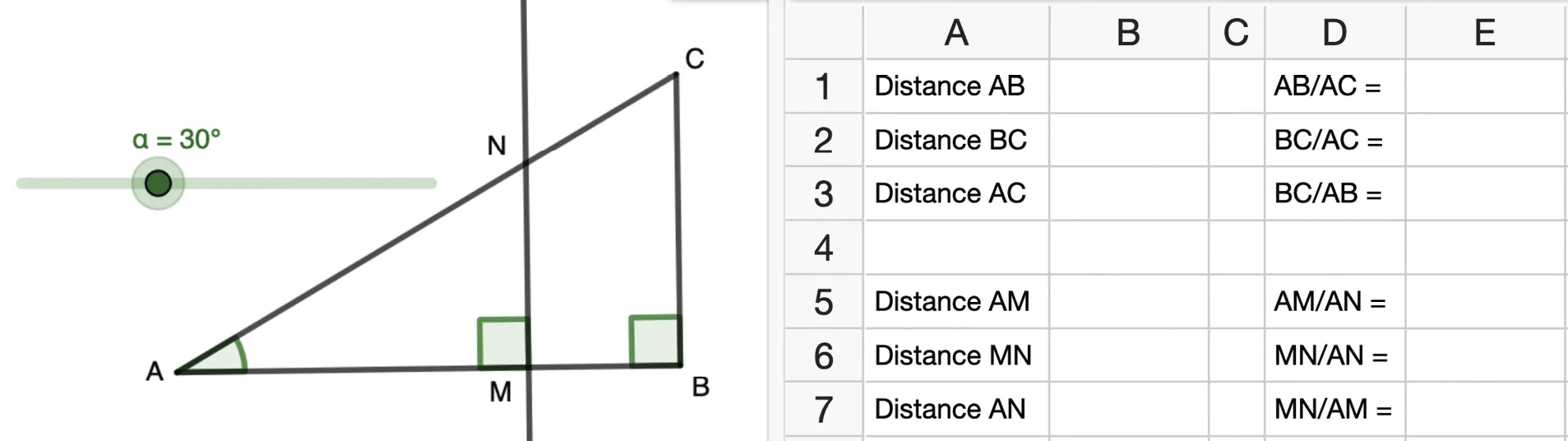
Grâce à un logiciel de géométrie dynamique, on trace un triangle \text{ABC} rectangle en \text{B} tel que la mesure de l'angle \widehat{\mathrm{BAC}} soit définie par un curseur que l'on fixe ici à 30° puis on place un point \text{M} appartenant à \text{[AB].} On trace ensuite la droite perpendiculaire à \text{[AB]} passant par \text{M.} On nomme enfin \text{N} le point d'intersection de cette droite avec le côté \text{[AC].}

1

Quelle est la nature du triangle \text{AMN} ?

2

Dans le tableau ci-dessus, quelles formules doit‑on entrer dans les colonnes B et E pour afficher les longueurs et rapports indiqués ? Que constate‑t‑on ?

3

Déplacer le point \text{M} et observer ces valeurs. Que peut‑on conjecturer ? Quel théorème permet de démontrer cette conjecture ?

4

Grâce au curseur, changer la valeur de l'angle \widehat{\mathrm{BAC}} en déplaçant le point \text{C.} Déplacer ensuite le point \text{M.} Cette conjecture est‑elle toujours vérifiée ?

On appelle ces trois quotients les cosinus, sinus et tangente de l'angle \widehat{\mathbf{B A C}}.
Que peut‑on dire de ces trois rapports ?

Nora regarde des avions décoller. L'angle entre le sol et la trajectoire rectiligne d'un avion au décollage est constant et mesure 40°. Nora se demande à quelle hauteur se trouvera l'avion lorsqu'il aura parcouru 1\:000 m dans les airs après son décollage.


Faire un schéma de la situation.

2

Identifier chacun des côtés du triangle rectangle par rapport à l'angle mesurant 40°.

3

Quelle relation trigonométrique permettrait de déterminer la longueur cherchée ?

Coup de pouce

Cosinus	Sinus	Tangente
Adjacent	Opposé	Opposé
Hypoténuse	Hypoténuse	Adjacent

4

En utilisant un produit en croix et les informations données, déterminer cette longueur.

Quelles sont les étapes permettant de calculer une longueur dans un triangle rectangle en s'aidant des relations trigonométriques ?

Faire un schéma de la situation.

2

Identifier chacun des côtés du triangle rectangle par rapport à l'angle dont on cherche la mesure.

3

Quelle relation trigonométrique permettrait de déterminer l'angle d'inclinaison ?

4

En utilisant les informations données, déterminer l'angle cherché à l'aide des fonctionnalités de la calculatrice.

Coup de pouce

Les touches Arcos, Arcsin et Arctan d'une calculatrice permettent de déterminer la mesure d'un angle.

Quelles sont les étapes permettant de calculer une mesure d'angle aigu dans un triangle rectangle en s'aidant des relations trigonométriques ?