Mathématiques 3e - 2021
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Nombres et calculs
Ch. 1
Nombres entiers
Ch. 2
Calcul numérique
Ch. 3
Calcul littéral
Ch. 4
Équations
Partie 2 : Organisation et gestion de données, fonctions
Ch. 5
Notion de fonction
Ch. 6
Fonctions affines
Ch. 7
Situations de proportionnalité
Ch. 8
Statistiques
Ch. 9
Probabilités
Partie 3 : Espace et géométrie
Ch. 10
Théorème de Thalès et triangles semblables
Ch. 11
Trigonométrie dans le triangle rectangle
Ch. 12
Transformations dans le plan et leurs effets
Ch. 13
Géométrie dans l'espace
Partie 4 : Mesures et grandeurs
Ch. 14
Mesures et grandeurs
Annexes
Scratch
Dossier brevet
Rappels, Index, Compétences
Révisions Genially
Calcul littéral
Plan de travail
Chapitre 11
Exercices
Entraînement
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Vérifier que les connaissances de base sont acquises.
Développer les connaissances.
Maîtriser les notions de manière approfondie.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Relations trigonométriques dans
le triangle rectangle
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
46 [Ch.1 - Mod.4]
\text{CED} est un triangle rectangle en \text{D.}

Compléter le tableau suivant, lorsque cela est possible, avec les angles correspondants.

Compléter le tableau suivant, lorsque cela est possible, avec les angles correspondants.
| Cosinus | Sinus | Tangente | |
|---|---|---|---|
| \frac{\textbf{CD}}{\textbf{CE}} | \widehat{\mathrm{DCE}} | ||
| \frac{\bm{\text{CD}}}{\bm{\text{ED}}} | |||
| \frac{\textbf{ED}}{\textbf{CE}} | |||
| \frac{\textbf{ED}}{\textbf{CD}} |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
47
DÉMO
[Ch.2 - Rais.3]
Soit \text{ABC} un triangle rectangle en \text{A.}
1. Faire un schéma.
Cliquez pour accéder à une zone de dessin
2. Donner la relation, en fonction des longueurs du triangle, permettant de calculer \sin\widehat{\text{ABC}} puis celle permettant de calculer \cos\widehat{\text{ACB}}.
3. En déduire que \sin\widehat{\text{ABC}} = \cos\widehat{\text{ACB}}.
4. Démontrer de même que \sin\widehat{\text{ACB}} = \cos\widehat{\text{ABC}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
48
[Rep.6 - Cal.3]
On donne les mesures des trois côtés d'un triangle rectangle \text{ABC :}
\text{AB = 45} cm, \text{AC = 60} cm et \text{BC = 75} cm.
1. Donner la formule, en fonction des longueurs du triangle, permettant de calculer \cos\widehat{\text{ABC}}.
\text{AB = 45} cm, \text{AC = 60} cm et \text{BC = 75} cm.
1. Donner la formule, en fonction des longueurs du triangle, permettant de calculer \cos\widehat{\text{ABC}}.
2.
Donner, sans calculatrice, \cos\widehat{\text{ABC}} sous
forme d'une fraction irréductible.
3. Donner, sans calculatrice, la valeur exacte de \cos\widehat{\text{ABC}}.
3. Donner, sans calculatrice, la valeur exacte de \cos\widehat{\text{ABC}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
49
[Rep.6 - Cal.3]
On donne les mesures des trois côtés d'un triangle rectangle \text{ABC :}\text{AB = 15} cm, \text{AC = 20} cm et \text{BC = 25} cm.
1. Donner la relation, en fonction des longueurs du triangle, permettant de calculer \sin\widehat{\text{ABC}}.
2. Donner, sans calculatrice, \sin\widehat{\text{ABC}} sous forme d'une fraction irréductible.
3. Donner, sans calculatrice, la valeur exacte de \sin\widehat{\text{ABC}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
50
[Rep.6 - Cal.3]
Les trois côtés d'un triangle rectangle \text{ABC} mesurent
\text{AB = 0{,}5} m,
\text{AC = 1{,}2} m et \text{BC = 1{,}3} m.
1. Donner la formule, en fonction des longueurs du triangle, permettant de calculer \tan\widehat{\text{ABC}}.
2. Donner, sans calculatrice, \tan\widehat{\text{ABC}} sous forme d'une fraction irréductible.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
51
Copie d'élève
[Mod.4]
Lorsque l'on connaît la mesure des angles aigus dans un triangle rectangle ainsi que la longueur d'un côté, on est capable de déterminer la mesure de chacun des autres côtés grâce aux relations trigonométriques.Compléter le tableau avec la relation trigonométrique adéquate.
Rémi a écrit ses réponses en rouge.
| Côté cherché | ||||
| Hypoténuse | Opposé | Adjacent | ||
| Côté connu | Hypoténuse | sinus | cosinus | |
| Opposé | tangente | tangente | ||
| Adjacent | cosinus | sinus | ||
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
52
[Rep.6 - Cal.3 - Mod.4]
Soit \text{DEF} un triangle rectangle en \text{D} tel que \text{DE = 0{,}9} m, \text{DF = 1{,}2} m et \text{EF = 1{,}5} m.
Donner les valeurs exactes du sinus, du cosinus et de la tangente de l'angle \widehat{\text{DFE}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
53
Démo
[Ch.3 - Rais.1 - Mod.10]
On a créé la feuille de calcul suivante.

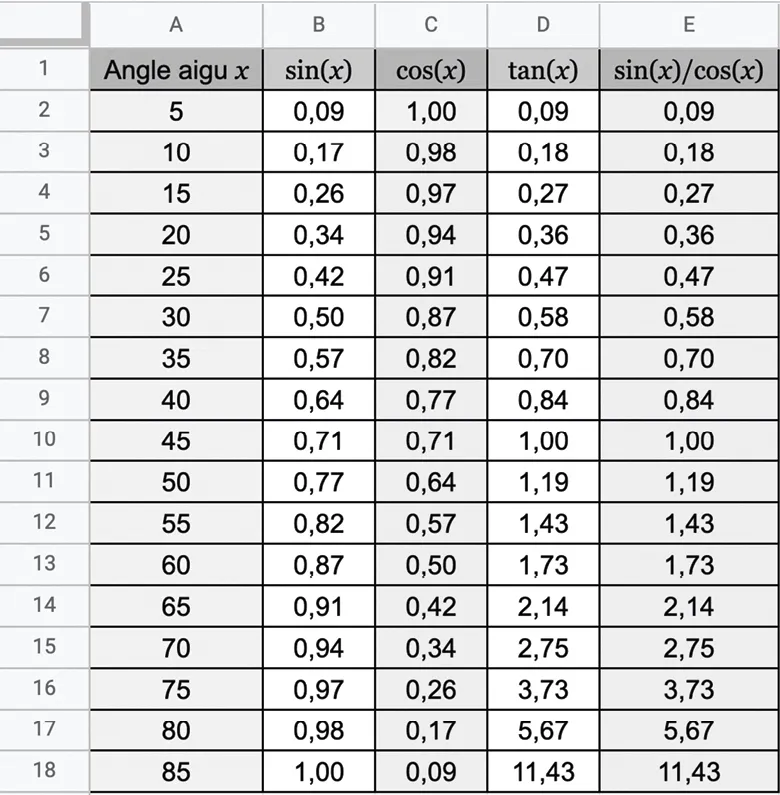
1. Quelle conjecture peut‑on émettre ?
2. On considère un triangle \text{ABC} rectangle en \text{A.} En utilisant les relations trigonométriques dans ce triangle, démontrer que cette conjecture est vraie quel que soit l'angle aigu \widehat{\text{ACB}}.
2. On considère un triangle \text{ABC} rectangle en \text{A.} En utilisant les relations trigonométriques dans ce triangle, démontrer que cette conjecture est vraie quel que soit l'angle aigu \widehat{\text{ACB}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
54
[Com.4 - Rais.4]
Soit \text{ABC} un triangle rectangle en \text{A} tel que \widehat{\text{ACB}} = 45°.
1. Faire un schéma à main levée.
1. Faire un schéma à main levée.
Cliquez pour accéder à une zone de dessin
2.
Que peut-on dire du triangle \text{ABC} ?
3. Démontrer que {\sin 45° = \cos 45°.}
3. Démontrer que {\sin 45° = \cos 45°.}
4.
On admet que, pour tout angle x, on a {\cos^{2}x + \sin^{2}x = 1} (voir pour une démonstration de cette propriété).
En déduire que {\sin 45°=\cos 45°=\sqrt{\frac{1}{2}}.}
5. De même, on admet que, pour tout angle x, {\tan x=\frac{\sin x}{\cos x}} (voir pour la démonstration de cette formule).
En déduire la valeur exacte de \tan45°.
En déduire que {\sin 45°=\cos 45°=\sqrt{\frac{1}{2}}.}
5. De même, on admet que, pour tout angle x, {\tan x=\frac{\sin x}{\cos x}} (voir pour la démonstration de cette formule).
En déduire la valeur exacte de \tan45°.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
55Démo
[Cal.3 - Rais.4]
L'objectif de cet exercice est de déterminer le sinus et le cosinus de certains
angles particuliers.
Soit \text{ABC} un triangle rectangle en \text{A} tel que \widehat\text{ACB} = 30°.
1. Faire une figure. On appelle \text{B} ^\prime le symétrique de \text{B} par rapport au point \text{A.}
Soit \text{ABC} un triangle rectangle en \text{A} tel que \widehat\text{ACB} = 30°.
1. Faire une figure. On appelle \text{B} ^\prime le symétrique de \text{B} par rapport au point \text{A.}
Cliquez pour accéder à une zone de dessin
2. Démontrer que le triangle \text{BCB}^\prime est un triangle équilatéral.
3. Dans le triangle \text{ABC} donner l'expression de \sin\widehat{\text{ACB}} en fonction des longueurs des côtés de ce triangle.
3. Dans le triangle \text{ABC} donner l'expression de \sin\widehat{\text{ACB}} en fonction des longueurs des côtés de ce triangle.
4.
En déduire que \sin 30°=\frac{1}{2}.
5. En procédant de la même manière, donner la valeur exacte de \cos 60°.
5. En procédant de la même manière, donner la valeur exacte de \cos 60°.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Calculer des longueurs et des mesures d'angles aigus
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
56
[Ch.1 - Com.1]
On cherche à déterminer la longueur de l'ombre d'un arbre de 15 m de haut projetée sur le sol lorsque le Soleil fait un angle de 42° avec l'horizontale.
1. Faire une figure à main levée de la situation.
1. Faire une figure à main levée de la situation.
Cliquez pour accéder à une zone de dessin
2. Déterminer la longueur de l'ombre projetée. Arrondir à l'unité.




Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
57
[Ch.1 - Com.1]
On cherche à déterminer la hauteur d'une tour qui projette une ombre de 96 m de long sur le sol lorsque le Soleil fait un angle de 52° avec l'horizontale.
1. Faire une figure à main levée de la situation.
Cliquez pour accéder à une zone de dessin
2. Déterminer la hauteur de la tour. Arrondir à l'unité.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
58
[Ch.1 - Ch.2 - Cal.5]

Quelle est la hauteur de la tour Eiffel ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
59
Copie d'élève
[Mod.3]
Soit \text{ABC} un triangle rectangle en \text{A} tel que \text{BC = 125} m et \widehat{\text{ACB}} = 26°. On donne \sin 26° \approx 0{,}4384. Calculer \text{AB.} Donner une valeur approchée au dixième. Voici la réponse proposée par Julien :
On sait que \text{ABC} est rectangle en \text{A.}
Or \sin \widehat{\text{ACB}}=\frac{\text{AB}}{\text{BC}} d'où \text{AB}=\frac{\text{BC}}{0{,}4384} \approx 285{,}1 m.
Or \sin \widehat{\text{ACB}}=\frac{\text{AB}}{\text{BC}} d'où \text{AB}=\frac{\text{BC}}{0{,}4384} \approx 285{,}1 m.
Indiquer l'erreur commise par Julien et proposer une correction à cet exercice.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
60
[Rep.6 - Rais.3]
Soit \text{JOYE} un rectangle tel que \widehat{\text{JOE}} = 40° et \text{JE} = 9 cm.
1. Dessiner la figure en vraie grandeur.
2. Déterminer une valeur approchée au dixième de la mesure de chacun des côtés du rectangle.
3. En déduire une valeur approchée de son aire au dixième près.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
61
[Ch.1 - Mod.4]

On cherche à déterminer l'angle formé parles rayons du Soleil avec l'horizontale lorsque l'ombre d'un immeuble de 24 m de haut projette sur le sol une ombre de 16 m de long.
1. Faire une figure à main levée de la situation.
2. Déterminer la mesure arrondie à l'unité de l'angle cherché.
Cliquez pour accéder à une zone de dessin
2. Déterminer la mesure arrondie à l'unité de l'angle cherché.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
62
[Ch.4 - Com.4]
Soit \text{ABCD} un rectangle tel que \text{AB = 70} m et \text{BC = 120} m.
1. Déterminer la mesure à l'unité de l'angle \widehat{\text{DAC}}.
2. En déduire la mesure à l'unité de l'angle \widehat{\text{CAB}}.
3. Déterminer la mesure à l'unité de chacun des angles formés par les diagonales et les côtés du rectangle.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
63
Inversé
[Com.1]
Écrire un énoncé d'exercice dont la
réponse attendue est : « La pente de la rampe
de skate avec l'horizontale est de 8°. »
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
64
[Rais.3]
Une échelle de 15{,}50 m arrive à 15{,}20 m de haut sur le mur vertical sur
lequel elle est posée.Déterminer, au degré près, la mesure de l'angle qu'elle fait avec ce mur.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
65
[Ch.1 - Rep.5 - Rais.3 - Com.3]
L'astronome grec Hipparque a mis au point, au IIe siècle av. J.‑C., une méthode pour
mesurer le rapport des distances entre la Terre, le Soleil et la Lune. Lorsque la Lune est exactement à l'un de ses quartiers, c'est‑à‑dire lorsqu'on en voit exactement la moitié, l'angle formé entre le Soleil, la Terre et la Lune est de 89{,}85° environ.
On connaît la distance entre la Terre et le Soleil : elle est de 149\:597\:870 km. C'est ce que l'on nomme l'UA (Unité Astronomique).

En s'aidant du schéma ci‑dessus et des informations données, déterminer la distance Terre‑Lune lorsque la Lune est exactement à l'un de ses quartiers.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
66
[Ch.2 - Mod.4]
Ce panneau de signalisation signifie que, pour tout déplacement horizontal de 100~m, la route monte de 10~m.


On veut déterminer à quel angle d'inclinaison par rapport à l'horizontale cette indication correspond.


On veut déterminer à quel angle d'inclinaison par rapport à l'horizontale cette indication correspond.
1. Faire un schéma à main levée de la situation.
2. Déterminer l'angle d'inclinaison de la route par rapport à l'horizontale. Arrondir au dixième.
Cliquez pour accéder à une zone de dessin
2. Déterminer l'angle d'inclinaison de la route par rapport à l'horizontale. Arrondir au dixième.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
67
[Ch.1 - Ch.4 - Rais.3]
Le calcul de la pente de toiture est spécifique
à chaque habitation. Ainsi, pour une toiture en chaume, la pente minimale est de 40 %.Cela signifie que, pour 1~m parcouru horizontalement, le toit s'élève de 0{,}40~m.
À quel angle en degré cette pente correspond‑elle ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
69
[Ch.2 - Ch.4 - Rais.2]
Benoît souhaite installer une tyrolienne au fond de son jardin pour ses enfants.Il désire accrocher le câble à deux arbres : au premier à une hauteur de 4,50 m et au second à une hauteur de 1 m. Les deux arbres sont éloignés l'un de l'autre de 28 m.
Quel angle va alors former le câble de la tyrolienne avec l'horizontale ? Arrondir au degré.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
68
[Ch.4 - Mod.4 - Rais.3]
Luca aménage une rampe de skate sur le parking de sa maison. Il fabrique ainsi une rampe de 1{,}92 m de long et de hauteur totale 30 cm.
Avec quel angle par rapport à l'horizontale Luca peut‑il compter skater ? Arrondir au degré.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
70
[Ch.2 - Mod.4]
Une route en ligne droite forme un angle de 3° avec l'horizontale.
1. À quelle pente, exprimée en pourcentage, cet angle de 3° correspond‑il ? Arrondir à l'unité.
2. Quelle distance faut‑il parcourir sur cette route pour s'élever de 100 m au‑dessus du point de départ ? Arrondir à l'unité.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
