Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Analyse
Ch. 1
Suites
Ch. 2
Fonctions
Ch. 3
Dérivation
Partie 2 : Statistiques et probabilités
Ch. 4
Fréquences conditionnelles et probabilités conditionnelles
Ch. 5
Variables aléatoires
Automatismes
Partie 3 : Géométrie
Ch. 6
Trigonométrie
Ch. 7
Produit scalaire
Ch. 8
Nombres complexes
Partie 4 : Analyse
Ch. 9
Compléments sur la dérivation
Ch. 10
Primitives
Révisions Genially
Chapitre 9
TP Info
Suite géométrique complexe
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Soient a et b deux nombres réels et q le nombre complexe défini par q=a+\mathrm{i}b.
On définit la suite de nombres complexes \left(z_{n}\right) vérifiant z_{0}=1 et la relation, valable pour tout entier naturel n, z_{n+1}=q z_{n}.
On choisit ici q=1+\mathrm{i}.
1. Calculer z_{1}, z_{2}, z_{3} et z_{4}.
2. En déduire \left|z_{1}\right|, \left|z_{2}\right|, \left|z_{3}\right| et \left|z_{4}\right|.
3. Déterminer le sens de variation de la suite \left(\left|z_{n}\right|\right).
4. Conjecturer, pour tout entier naturel n, une expression de z_{n} en fonction de n.
On définit la suite de nombres complexes \left(z_{n}\right) vérifiant z_{0}=1 et la relation, valable pour tout entier naturel n, z_{n+1}=q z_{n}.
Questions préliminaires
On choisit ici q=1+\mathrm{i}.
1. Calculer z_{1}, z_{2}, z_{3} et z_{4}.
2. En déduire \left|z_{1}\right|, \left|z_{2}\right|, \left|z_{3}\right| et \left|z_{4}\right|.
3. Déterminer le sens de variation de la suite \left(\left|z_{n}\right|\right).
4. Conjecturer, pour tout entier naturel n, une expression de z_{n} en fonction de n.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Se familiariser avec les suites géométriques complexes et étudier le sens de variation de la suite des modules, en utilisant une des deux méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode de résolution 1
Geogebra
On choisit ici q=\frac{3}{4}+\frac{1}{2} \mathrm{i}.
On veut créer un tableau donnant les différentes valeurs de z_n, \operatorname{Re}\left(z_{n}\right), \operatorname{Im}\left(z_{n}\right) et \left|z_{n}\right| pour n allant de 0 à 15, puis afficher la ligne brisée formée par les points \text{A}_n d'affixe z_n.
1. Reproduire le tableau suivant dans GeoGebra.
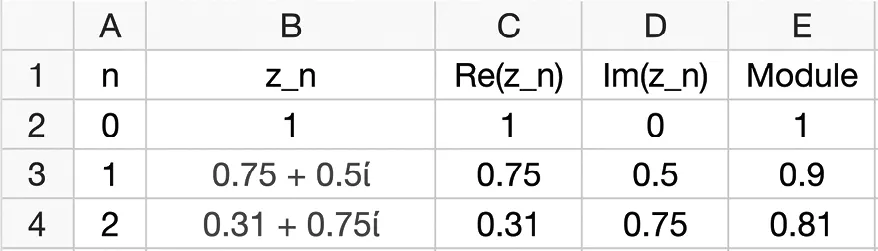
2. a. On a saisi dans la cellule B3 la formule \color{purple}\bf{=(0.75+0.5i)*B2} et dans la cellule C2 la formule \color{purple}\bf{=Re(B2)}.
Quelles formules doit‑on saisir dans les cellules D2 et E2 pour obtenir toutes les valeurs voulues en étirant ces formules vers le bas ?
b. Créer une ligne brisée à partir des colonnes C et D et observer le graphique obtenu. Quelle figure observe‑t‑on ?
3. Quel est le sens de variation de \left(\left|z_{n}\right|\right) ?
4. Que se passe‑t‑il pour \left(\left|z_{n}\right|\right) lorsque l'on choisit q = \text{i} ?
On veut créer un tableau donnant les différentes valeurs de z_n, \operatorname{Re}\left(z_{n}\right), \operatorname{Im}\left(z_{n}\right) et \left|z_{n}\right| pour n allant de 0 à 15, puis afficher la ligne brisée formée par les points \text{A}_n d'affixe z_n.
1. Reproduire le tableau suivant dans GeoGebra.
Le zoom est accessible dans la version Premium.
GeoGebra
2. a. On a saisi dans la cellule B3 la formule \color{purple}\bf{=(0.75+0.5i)*B2} et dans la cellule C2 la formule \color{purple}\bf{=Re(B2)}.
Quelles formules doit‑on saisir dans les cellules D2 et E2 pour obtenir toutes les valeurs voulues en étirant ces formules vers le bas ?
b. Créer une ligne brisée à partir des colonnes C et D et observer le graphique obtenu. Quelle figure observe‑t‑on ?
3. Quel est le sens de variation de \left(\left|z_{n}\right|\right) ?
4. Que se passe‑t‑il pour \left(\left|z_{n}\right|\right) lorsque l'on choisit q = \text{i} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode de résolution 2
Python
1. Le code suivant définit une fonction qui permet de calculer les différents termes de la suite \left(z_{n}\right) avec q = 1 + \text{i}.
a. Vérifier que ce programme permet de confirmer les calculs de la question préliminaire.
b. Modifier le code afin qu'il corresponde à l'étude de la suite \left(z_{n}\right) lorsque q=\frac{3}{4}+\frac{1}{2} \mathrm{i}.
2. Écrire une fonction permettant de renvoyer la partie réelle et la partie imaginaire de z_{n} lorsqu'on saisit n.
3. Écrire une boucle qui calcule et affiche les valeurs successives de \left|z_{n}\right| , pour n allant de 0 à 10. Conjecturer alors le sens de variation de \left(\left|z_{n}\right|\right).
4. Que remarque‑t‑on pour \left(\left|z_{n}\right|\right) lorsqu'on prend q=\mathrm{i} ?
from math import sqrt
q = complex(1, 1)
def suite(n):
z = 1
for k in range(n):
z = z*q
return z
a. Vérifier que ce programme permet de confirmer les calculs de la question préliminaire.
b. Modifier le code afin qu'il corresponde à l'étude de la suite \left(z_{n}\right) lorsque q=\frac{3}{4}+\frac{1}{2} \mathrm{i}.
Remarque
Dans le langage Python, le nombre complexe \text{i} est noté \text{j}.
2. Écrire une fonction permettant de renvoyer la partie réelle et la partie imaginaire de z_{n} lorsqu'on saisit n.
Aide
Les commandes z.real et z.imag permettent d'obtenir la partie réelle et la partie imaginaire de z.
3. Écrire une boucle qui calcule et affiche les valeurs successives de \left|z_{n}\right| , pour n allant de 0 à 10. Conjecturer alors le sens de variation de \left(\left|z_{n}\right|\right).
4. Que remarque‑t‑on pour \left(\left|z_{n}\right|\right) lorsqu'on prend q=\mathrm{i} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On admet que si \left(u_{n}\right) est une suite géométrique de raison q^{\prime}, alors, pour tout entier naturel n, u_{n}=u_{0} \times q^{\prime n}.
1. Ce résultat est‑il cohérent avec la formule conjecturée dans la question préliminaire 4 ?
2. En déduire, pour tout entier naturel n, une expression de \left|z_{n}\right| en fonction de n lorsque q=\frac{3}{4}+\frac{1}{2} \mathrm{i}.
1. Ce résultat est‑il cohérent avec la formule conjecturée dans la question préliminaire 4 ?
2. En déduire, pour tout entier naturel n, une expression de \left|z_{n}\right| en fonction de n lorsque q=\frac{3}{4}+\frac{1}{2} \mathrm{i}.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah