Enseignement mathématique 1re
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Exercices rituels et automatismes
Exercices rituels
Automatismes
Partie 1 - Information chiffrée
Ch. 1
Analyse de l'information chiffrée
Partie 2 - Probabilités
Ch. 2
De la statistique aux probabilités
Partie 3 - Phénomènes d’évolution
Ch. 3
Croissance linéaire
Ch. 4
Croissance exponentielle
Partie 4 - Dérivation
Ch. 5
Variations instantanées
Ch. 6
Variations globales
GeoGebra
Chapitre 3
Pour aller plus loin
Terme général d'une suite arithmétique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Cette double-page permet d'approfondir les notions de ce chapitre et de travailler de façon différenci�ée avec les élèves de la classe, notamment avec les plus à l'aise en mathématiques ou bien avec celles et ceux qui souhaiteraient choisir l'option mathématiques complémentaires en terminale.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Cours
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On considère une suite u.
- Pour tout entier naturel n, le terme u(n) d'une suite u est noté un et on note \left(u_{n}\right) la suite u.
- Une suite arithmétique u de raison r vérifie pour tout entier naturel n : {u_{n+1}=u_{n}+r}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriétés
Soit \left(u_{n}\right) une suite arithmétique de raison r et de premier terme u_{0}.
1. Pour tout entier {n \in \mathbb{N}}, {u_{n}=n \times r+u_{0}}.
2. Pour tous entiers naturels n et p, {u_{n}=(n-p) \times r+u_{p}}.
1. Pour tout entier {n \in \mathbb{N}}, {u_{n}=n \times r+u_{0}}.
2. Pour tous entiers naturels n et p, {u_{n}=(n-p) \times r+u_{p}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Soit {\left(u_{n}\right)} la suite arithmétique de raison r = -2 telle que u_{5}=7.
Pour tout entier naturel n, {u_{n}=(n-5) \times r+u_{5}}, soit
Pour tout entier naturel n, {u_{n}=(n-5) \times r+u_{5}}, soit
u_{n}=-2(n-5)+7=-2 n+17.
On en déduit que {u_{0}=-2 \times 0+17=17}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercices
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
62
Soit \left(u_{n}\right) la suite arithmétique définie sur \mathrm{N} par {u_{n}=5 n-4}.
Exprimer u_{n+1} en fonction de n.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
63
Soit \left(u_{n}\right) la suite arithmétique définie sur \mathrm{N} par {u_{n}=1-n \sqrt{2}}.
Calculer {u_{n+1}-u_{n}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
64
Soit \left(u_{n}\right) une suite arithmétique vérifiant, pour tout entier naturel n, {u_{n+1}=u_{n}+\frac{1}{2}}. Exprimer u_{n+3} en fonction de u_{n}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
65
Soit \left(u_{n}\right) la suite arithmétique de raison r=\frac{3}{5} telle que u_{4}=-\frac{2}{5}.
Calculer les termes de rang 9 et de rang 2 de cette suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
66
Soit \left(u_{n}\right) la suite arithmétique telle que u_{2}=3 et u_{12}=-1.
Déterminer la raison r et le premier terme u_{0} de cette suite
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
67
Pour chacune des suites suivantes, calculer \mathrm{u}_{20}.
1. La suite \left(u_{n}\right) est artimétique de raison r=3 et telle que u_{7}=12.
2. La suite \left(u_{n}\right) est artimétique de raison r=5 et telle que u_{25}=17.
3. La suite \left(u_{n}\right) est définie par {\left\{\begin{array}{c} u_{0}=3 \\ u_{n+1}=u_{n}+7 \end{array}\right.} pour {n \in \mathbb{N}}
4. La suite \left(u_{n}\right) est définie par {\left\{\begin{array}{c} u_{1}=-2 \\ u_{n+1}=u_{n}-4 \end{array}\right.} pour {n \in \mathbb{N}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
68
Kalyam place une somme d'argent u_{0} au taux simple annuel de 5 % ; c'est-à-dire que chaque année, la somme placée augmentera de 5 % de la somme initiale. Pour tout entier naturel n, un désigne le capital de Kalyam n années après son placement.
1. Déterminer u_{1} et u_{2} en fonction de u_{0}.
2. Exprimer u_{n+1} en fonction de u_{n} et de u_{0}.
3. En justifiant, déterminer une expression de u_{n} en fonction de n et de u_{0}.
4. Cinq ans après avoir placé son argent, Kalyam possède 1\:250 €. Quelle somme d'argent avait-il placé au départ ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
69
Dans le jardin de Yoann, se trouve un puits de 15,7 m de profondeur. Toutes les heures, il creuse 1,2 m. On note u_n la profondeur du puits au bout de \mathrm{n} heures.


1. Justifier que \left(u_{n}\right) est une suite arithmérique dont on précisera la raison et le premier terme u_{0}.
2. Résoudre u_{n} \geqslant 30. Interpréter ce résultat.
3. Compléter le programme Python ci-dessous afin de retrouver le résultat obtenu à la question 2.
def seuil() : u = 15.7 n = 0 while ... : u = ... n = ... return(n)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
70
On donne ci-dessous un programme rédigé à l'aide de Python.


1. Ce programme est associé à une suite arithmétique \left(u_{n}\right). Préciser la raison r et le premier terme u_{0} de cette suite.
2. a. Quel est l'objectif de ce programme ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
71
Rayane loue un appartement à Bordeaux. Son contrat de location débute le 1er juin 2022 avec un loyer de 503 € qui augmente ensuite de 32 € tous les ans. On note u_{n} le loyer de l'appartement de Rayane, en euro, au bout de \mathrm{n} années après le 1er juin 2022. On a donc u_{0}=503.
1. On admet que \left(u_{n}\right) est une suite arithmétique. Donner la raison r de cette suite.
2. Quel loyer Rayane devra-t-il payer au 1er juin 2029 ?
3. Afin d'y voir plus clair dans ses dépenses, Rayane réalise la feuille de calcul ci-dessous.

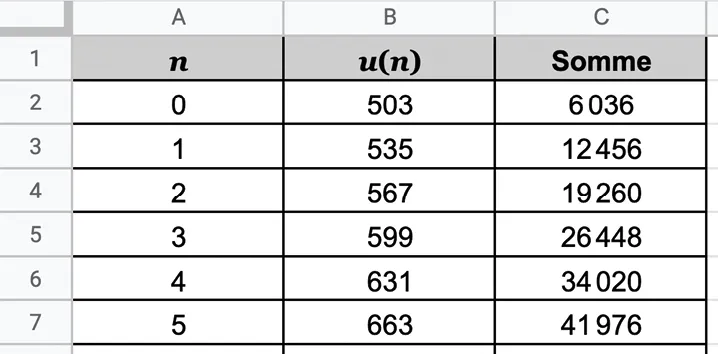
a. Quelle formule Rayane a-t-il entrée dans la cellule B3 puis étirée vers le bas pour remplir automatiquement la colonne B ?
b. Sachant que {6\:036=503 \times 12}, à quoi correspond la valeur calculée dans la cellule C2 ?
c. À quoi correspond la valeur dans la cellule C3 ? Comment a-t-elle été calculée ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
72
On souhaite démontrer la propriété suivante : « Si \left(u_{n}\right) est une suite arithmétique de raison r, alors, pour tous entiers naturels n et p,
{u_{n}=(n-p) r+u_{p}} ».
1. Rappeler l'expression de u_{n} en fonction de u_{0}, de n et de r.
2. Exprimer de même u_{p} en fonction de u_{0}, de p et de r.
3. En déduire une expression de u_{0} en fonction de u_{p}, de p et de r.
4. Conclure.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
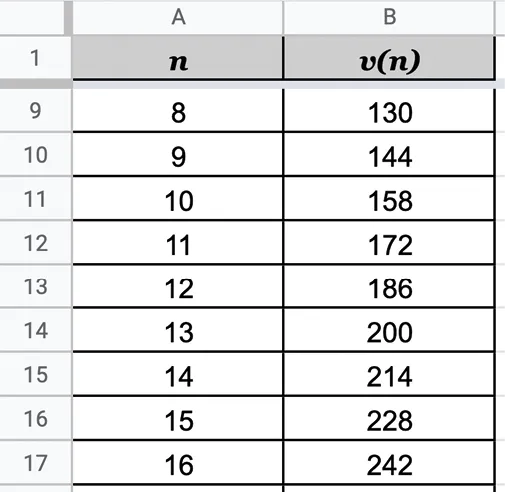
73
La suite \left(v_{n}\right) est une suite arithmétique dont on a calculé les termes à l'aide d'un tableur.
1. Déterminer la raison de la suite \left(v_{n}\right).
2. Calculer le premier terme v_{0}.
3. Calculer v_{20} de deux façons différentes.
2. Calculer le premier terme v_{0}.
3. Calculer v_{20} de deux façons différentes.

Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
