Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Exercices rituels et automatismes
Exercices rituels
Automatismes
Partie 1 - Information chiffrée
Ch. 1
Analyse de l'information chiffrée
Partie 2 - Probabilités
Ch. 2
De la statistique aux probabilités
Partie 3 - Phénomènes d’évolution
Ch. 3
Croissance linéaire
Ch. 4
Croissance exponentielle
Partie 4 - Dérivation
Ch. 5
Variations instantanées
Ch. 6
Variations globales
GeoGebra
Chapitre 4
Exercices d'entraînement
1. Suites géométriques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27
On considère la suite u définie par u(0)=0,5 et, pour tout entier naturel n, u(n+1)=3 \times u(n).
1. Calculer u(1), u(2) et u(3).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28
Exercice inversé
Écrire l'énoncé d'un exercice sur les suites géométriques dont les réponses sont les suivantes.
1. u(1) = 10, u(2) = 50 et u(3) = 250.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29
On considère la suite u définie par u(0) = 3 et, pour tout entier naturel n, u(n+1)=4 \times u(n).
1. Calculer u(1), u(2) et u(3).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
30
Environnement
La quantité d'énergie, en TWh, consommée chaque année par les data centers dans le monde depuis 2018 peut être modélisée par la suite géométrique définie par u(0) = 200 et u(n+1)=1,6 \times u(n), où n représente le nombre d'années écoulées depuis l'année 2018.
Le zoom est accessible dans la version Premium.
1. Quelle est la raison de cette suite géométrique ?
2. Selon cette modélisation, quelle quantité d'énergie a été consommée par les data centers en 2021 ?
3. On estime qu'à Paris, en 2021, un habitant consomme en moyenne 1,82 MWh/an soit 1,82 \times 10^{-6} TWh/an. D'après la région Île-de-France, Paris comptait 2\:175\:061 habitants en 2021.
Au cours de cette année, la population parisienne a-t-elle consommé plus ou moins d'énergie que les data centers ?
Au cours de cette année, la population parisienne a-t-elle consommé plus ou moins d'énergie que les data centers ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
31
Lorsqu'une personne prend connaissance d'une rumeur, elle partage cette rumeur avec deux autres personnes qui ne la connaissaient pas.
1. Montrer que la propagation d'une rumeur peut être modélisée par une suite géométrique dont on précisera la raison.
2. Dans la situation de l'énoncé, la rumeur va-t-elle gagner ou perdre en intensité ? Justifier.
3. En étudiant de plus près le comportement des personnes, on remarque que 80 % des personnes qui prennent connaissance de la rumeur ne la partagent pas. On suppose que 10\:000 personnes sont au courant de la rumeur. Justifier que la modélisation de la propagation de la rumeur est toujours une suite géométrique et en donner la nouvelle raison.
4. La rumeur va-t-elle gagner ou perdre en intensité ? Justifier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
32
Jean a calculé les sept premiers termes d'une suite géométrique. Malheureusement il a effacé par erreur certains d'entre eux.
u(0)=8
u(2)=2
u(2)=2
u(5)=0,25
Aider Jean à retrouver les termes manquants.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
33
En NSI
Un microprocesseur est la partie d'un ordinateur qui permet d'exécuter les instructions et de traiter les données d'un programme.
Un transistor est un des composants du microprocesseur : plus le microprocesseur contient de transistors, plus il peut réaliser des opérations complexes et traiter des nombres de grande taille.
En 1965, Gordon Moore conjecture que le nombre de transistors sur un microprocesseur nouvelle génération doublera tous les deux ans. En 1972, le processeur « 8008 » possédait 3\:500 transistors.
Un transistor est un des composants du microprocesseur : plus le microprocesseur contient de transistors, plus il peut réaliser des opérations complexes et traiter des nombres de grande taille.
En 1965, Gordon Moore conjecture que le nombre de transistors sur un microprocesseur nouvelle génération doublera tous les deux ans. En 1972, le processeur « 8008 » possédait 3\:500 transistors.
1. Justifier que, selon la loi de Moore, le nombre de transistors sur un microprocesseur à l'année 1972+2n est modélisé par une suite géométrique dont on donnera le premier terme et la raison.
2. En 1974 est sorti le processeur « 8080 ». Selon la modélisation précédente, combien de transistors contenait-il ?
2. En 1974 est sorti le processeur « 8080 ». Selon la modélisation précédente, combien de transistors contenait-il ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
34
La loi de Moore, définie dans l'exercice précédent, conjecture que le nombre de transistors dans un microprocesseur est modélisé par la suite géométrique \mathrm{p} de premier terme p(0)=3\:500 et de raison 2.
On donne la feuille de calcul ci-dessous.
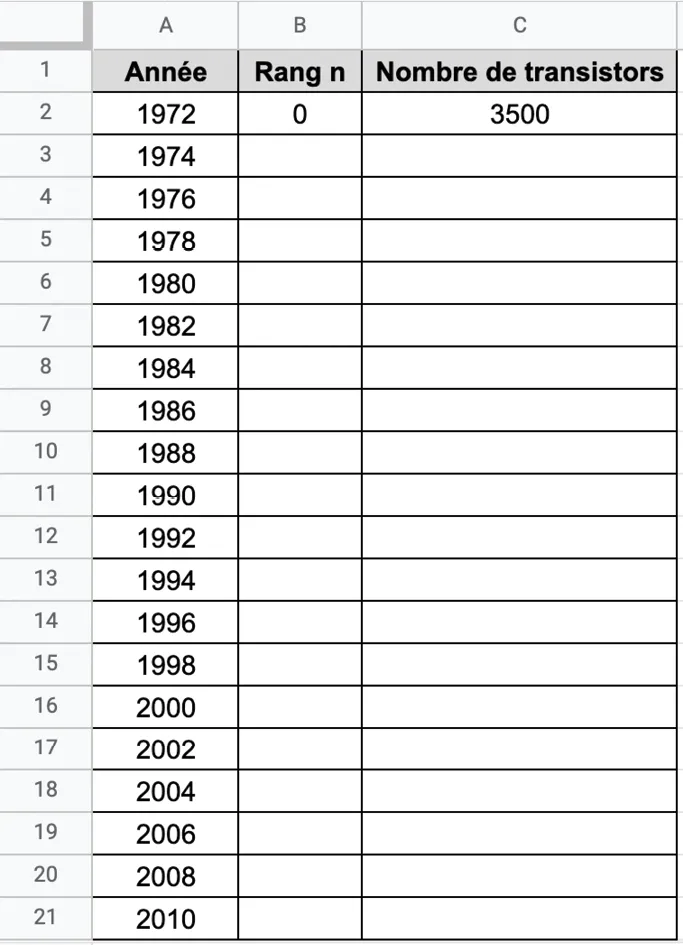
On donne la feuille de calcul ci-dessous.
Le zoom est accessible dans la version Premium.
1. Quelle formule doit-on saisir en C3, puis étirer vers le bas, pour obtenir le nombre de transistors dans les microprocesseurs à l'année voulue ?
2. Compléter cette feuille de calcul, soit en utilisant un tableur, soit en utilisant la calculatrice, pour calculer une estimation du nombre de transistors sur un microprocesseur en 2010.
3. On rappelle que, p étant une suite géométrique, on a, pour tout entier naturel n, p(n)=p(0) \times q^{n}. À l'aide de cette formule, calculer le nombre de transistors dans un microprocesseur en 2010.
4. Une recherche Internet montre qu'en 2010, on comptait environ 1\:170\:000\:000 transistors par microprocesseur.
Que peut-on dire de la loi de Moore ? Donne-t-elle des résultats exacts ? De bons ordres de grandeur ?
2. Compléter cette feuille de calcul, soit en utilisant un tableur, soit en utilisant la calculatrice, pour calculer une estimation du nombre de transistors sur un microprocesseur en 2010.
3. On rappelle que, p étant une suite géométrique, on a, pour tout entier naturel n, p(n)=p(0) \times q^{n}. À l'aide de cette formule, calculer le nombre de transistors dans un microprocesseur en 2010.
4. Une recherche Internet montre qu'en 2010, on comptait environ 1\:170\:000\:000 transistors par microprocesseur.
Que peut-on dire de la loi de Moore ? Donne-t-elle des résultats exacts ? De bons ordres de grandeur ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
35
On considère la suite géométrique \mathrm{u} définie pour tout entier naturel \mathrm{n}, de premier terme u(0)=8 et de raison q=1,5.
1. Calculer u(1), u(2) et u(3).
2. Représenter graphiquement le nuage de points associé aux quatre premiers termes de cette suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
36
On considère les suites géométriques k et p définies par k(0)=1 et p(0)=8 et les relations, valables pour tout entier naturel n, k(n+1)=1,5 \times k(n) et p(n+1)=0,8 \times p(n).
Associer à chaque suite la représentation graphique qui lui correspond en utilisant la méthode indiquée.
Le zoom est accessible dans la version Premium.
1. En utilisant une des valeurs prises par chacune des suites.
2. En utilisant les variations des suites étudiées.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
37
Parmi les suites géométriques suivantes, définies pour tout n \in \mathbb{N}, lesquelles sont croissantes ? Justifier.
1. u(0)=4 et {u(n+1)=0,5 \times u(n)}
2. v(0)=0,5 et {v(n+1)=4 \times v(n)}
3. w(0)=4 et {w(n+1)=\sqrt{2} \times w(n)}
4. z(0)=4 et {z(n+1)=\frac{1}{4} \times z(n)}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
38
Fil rouge
La quantité de carbone 14 d'un organisme biologique vivant est stable et vaut \mathrm{A}. À sa mort, on estime que cette quantité diminue approximativement de 1,24 % par siècle.
On note \mathrm{C}(n) la quantité de carbone 14 dans un organisme n siècles après sa mort. Ainsi, \mathrm{C}(0)=\mathrm{A}
1. Justifier que la suite \mathrm{C} est une suite géométrique dont on précisera la raison.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
39
Un triangle de Sierpinski se dessine en commençant par tracer un triangle équilatéral dont l'aire vaut 1. À la première étape, on marque le milieu de chacun de ses côtés et on enlève le triangle au centre. Puis on répète l'opération avec les trois triangles restants et ainsi de suite.
Le zoom est accessible dans la version Premium.
1. Quelle est l'aire de la partie colorée à l'étape initiale ? À l'étape 1 ? À l'étape 2 ?
2. Par quelle opération passe-t-on de l'aire colorée de l'étape n à l'aire colorée de l'étape n+1 ?
3. On note \mathrm{A} la suite qui modélise l'aire colorée à chaque étape.
Justifier que \mathrm{A} est une suite géométrique dont on précisera le premier terme et la raison.
2. Par quelle opération passe-t-on de l'aire colorée de l'étape n à l'aire colorée de l'étape n+1 ?
3. On note \mathrm{A} la suite qui modélise l'aire colorée à chaque étape.
Justifier que \mathrm{A} est une suite géométrique dont on précisera le premier terme et la raison.
4. Exprimer, pour tout entier naturel n, \mathrm{A(n)} en fonction de n.
5. En utilisant la calculatrice ou le tableur, déterminer la plus petite valeur de n telle que \mathrm{A(n)} \lt 0,1.
5. En utilisant la calculatrice ou le tableur, déterminer la plus petite valeur de n telle que \mathrm{A(n)} \lt 0,1.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah