Soient a et b deux réels.
m>0 : a \lt b \Leftrightarrow m a \lt m b
\Leftrightarrow m a+p \lt m b+p \Leftrightarrow f(a) \lt f(b)
donc f est strictement croissante.

m \lt 0 : a \lt b \Leftrightarrow m a>m b
\Leftrightarrow m a+p>m b+p \Leftrightarrow f(a)>f(b)
donc f est strictement décroissante.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Logique

On peut utiliser un raisonnement par l'absurde pour démontrer les réciproques.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Propriété

f est une fonction affine impaire si et seulement si f est une fonction linéaire.
f est une fonction affine paire si et seulement si f est une fonction constante.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Démonstration

Voir exercice

p. 111

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Application et méthode

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Utiliser les variations

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Énoncé

Soit a \in[-3\: ;-2] et g une fonction affine définie sur \mathbb{R} par g(x)=-4 x-5. Déterminer un encadrement de g(a).

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Méthode

1. On vérifie les variations de la fonction g .
2. La fonction est décroissante donc deux nombres et leur image sont classés dans l'ordre inverse.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Solution

La fonction affine g est strictement décroissante car m = -4 et -4 \lt 0 donc :
-3 \leqslant a \leqslant-2
\Leftrightarrow g(-3) \geqslant g(a) \geqslant g(-2)
\Leftrightarrow 7 \geqslant g(a) \geqslant 3

Pour s'entraîner

Exercices 25
p. 105, 62
p. 109 et 63
p. 110.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Utiliser la parité

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Énoncé

h est une fonction affine impaire telle que h(3) = 5. En déduire l'expression de h en fonction de x \in \mathbb{R}.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Méthode

1. On détermine de quel type de fonction affine il s'agit en utilisant la propriété.
2. En utilisant la bonne définition et les valeurs de l'énoncé, on détermine l'expression de la fonction cherchée.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Solution

h est une fonction affine et impaire : elle est donc linéaire.
Ainsi, il existe k \in \mathbb{R} tel que, pour tout x \in \mathbb{R}, h(x)=k x.
Puisque h(3)=5 alors 3 k=5 d'où k=\dfrac{5}{3}.
Pour tout x \in \mathbb{R}, h(x)=\dfrac{5}{3} x.

Pour s'entraîner

Exercices 25
p. 105.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

B
Signes

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Propriété

1. Si m \neq 0, alors f(x)=0 \Leftrightarrow x=-\dfrac{p}{m}.

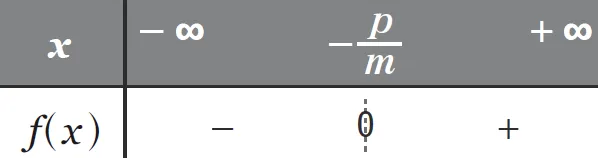
2. Si m > 0, alors {f(x>0 \Leftrightarrow x>-\dfrac{p}{m}}.

m > 0

Tableau: comportement fonction affine. Valeurs f(x) selon x. Illustration mathématique.

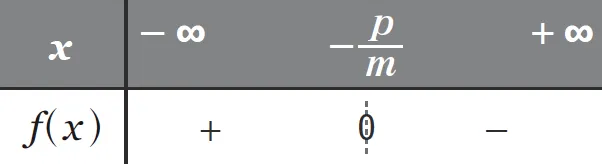
3. Si m > 0, alors {f(x)\lt0 \Leftrightarrow x\lt-\dfrac{p}{m}}.

m \lt 0

Tableau: étude mathématique d'une fonction affine, montrant l'évolution de f(x) selon x.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Remarque

Si m = 0, f est du signe de p.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Démonstration

Voir exercice

p. 111

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Conséquence

Pour étudier le signe d'un produit ou d'un quotient de deux fonctions affines, on étudiera le signe de chacune des fonctions dans un même tableau de signes et on conclura à l'aide de la propriété des signes d'un produit ou d'un quotient.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Remarque

Faire attention à l'ensemble de définition de la fonction pour un quotient.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Application et méthode

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Signes d'une fonction affine

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Énoncé

Dresser le tableau de signes de la fonction h définie sur \mathbb{R} par h(x) = -3x - 4.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Méthode

1. On vérifie les variations de h.
2. On calcule la valeur qui annule h.
3. On complète le tableau de signes à l'aide de 1. et 2.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Solution

h est strictement décroissante et h(x)=0 \Leftrightarrow x=-\dfrac{-4}{-3}=-\dfrac{4}{3}

Tableau: étude de fonction affine, signe de h(x) selon les valeurs de x. Valeurs de x : -∞, -4/3, +∞. Signes de h(x) : +, 0, -.

Pour s'entraîner

Exercices 26
p. 105 et 65
p. 110

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Signe d'un produit

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Énoncé

Résoudre l'inéquation (3 x+2)(-2 x-1) \leqslant 0.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Méthode

1. On détermine le signe de chaque facteur en utilisant la méthode précédente.
2. On résume le signe du produit sur la dernière ligne.
3. On donne l'ensemble des solutions.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Solution

x \mapsto 3 x+2 est croissante sur \mathbb{R} et (3 x+2)=0 \Leftrightarrow x=\dfrac{-2}{3}. x \mapsto-2 x-1 est décroissante sur \mathbb{R} et -2 x-1=0 \Leftrightarrow x=\dfrac{-1}{2}. En résumé :

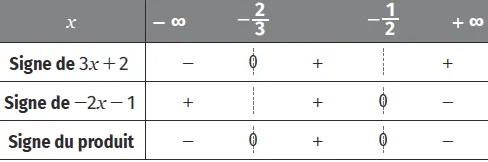
Tableau d'étude de signe des fonctions affines 3x+2 et -2x-1, montrant le signe de leur produit selon les valeurs de x.

Ainsi, \left.(3 x+2)(-2 x-1) \leqslant 0 \Leftrightarrow x \in]-\infty ; \frac{-2}{3}\right] \cup\left[\frac{-1}{2} ;+\infty[\right.

Pour s'entraîner

Exercices 27
p. 105, 71
p. 110 et 72
p. 111

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.

Mathématiques 2de

Étude d'une fonction affine

AVariation et parité

Remarque

Logique

Utiliser les variations

Méthode

Utiliser la parité

Méthode

BSignes

Remarque

Remarque

Signes d'une fonction affine

Méthode

Signe d'un produit

Méthode

Une erreur sur la page ? Une idée à proposer ?

A
Variation et parité

B
Signes