Physique-Chimie Terminale Spécialité
Mes Pages
Préparation aux épreuves du Bac
1. Constitution et transformations de la matière
Ch. 1
Modélisation des transformations acide-base
Ch. 2
Analyse physique d'un système chimique
Ch. 3
Méthode de suivi d'un titrage
Ch. 4
Évolution temporelle d'une transformation chimique
Ch. 5
Évolution temporelle d'une transformation nucléaire
BAC
Thème 1
Ch. 6
Évolution spontanée d'un système chimique
Ch. 7
Équilibres acide-base
Ch. 8
Transformations chimiques forcées
Ch. 9
Structure et optimisation en chimie organique
Ch. 10
Stratégies de synthèse
BAC
Thème 1 bis
2. Mouvement et interactions
Ch. 11
Description d'un mouvement
Ch. 12
Mouvement dans un champ uniforme
Ch. 13
Mouvement dans un champ de gravitation
Ch. 14
Modélisation de l'écoulement d'un fluide
BAC
Thème 2
3. Conversions et transferts d'énergie
Ch. 15
Étude d’un système thermodynamique
Ch. 16
Bilans d'énergie thermique
BAC
Thème 3
4. Ondes et signaux
Ch. 17
Propagation des ondes
Ch. 18
Interférences et diffraction
Ch. 19
Lunette astronomique
Ch. 20
Effet photoélectrique et enjeux énergétiques
Ch. 21
Évolutions temporelles dans un circuit capacitif
BAC
Thème 4
Annexes
Ch. 22
Méthode
Chapitre 2
Cours
Analyse physique d'un système chimique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Conductimétrie
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
AConductance d'une portion de solution
Une portion de solution ionique placée entre deux plaques métalliques
se comporte comme un conducteur ohmique.
Plutôt que la résistance R, on utilise en chimie la conductance G exprimée en siemens (S) :
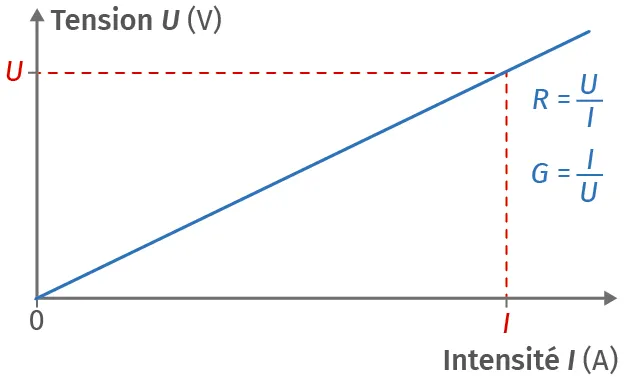
La tension U appliquée entre deux plaques métalliques plongeant dans la solution est proportionnelle à l'intensité I du courant dans le circuit, selon la loi d'Ohm U = R\ ·\ I.
Plutôt que la résistance R, on utilise en chimie la conductance G exprimée en siemens (S) :
G=\frac{1}{R}
G : \text{conductance (S)} \\
R: \text{résistance }(\Omega)
La conductance G dépend de la géométrie de la cellule de mesure. Si les plaques sont plus espacées, ou si leur surface est plus petite, alors la conductance G est plus faible.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 1Caractéristique illustrant la loi d'Ohm
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 2Cellule de mesure d'un conductimètre
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BConductivité d'une solution
La conductivité \sigma d'une solution est une grandeur caractéristique de la solution dépendant de sa nature, de sa concentration et de la température. En revanche, elle est indépendante de la cellule de mesure :
\sigma=G\ ·\frac{l}{S}
\sigma : conductivité (S·m-1)
G : conductance (S)
l : distance entre les plaques (m)
S : surface des plaques (m2)
G : conductance (S)
l : distance entre les plaques (m)
S : surface des plaques (m2)
Cette relation est souvent simplifiée sous la forme :
\sigma=\frac{G}{k}
k : constante de la cellule (m)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Attention à l'unité utilisée pour les concentrations dans la loi de Kohlrausch : elles doivent être exprimées en (mol·m-3).
- Conversion d'unité : 1 mol·m-3 = 10-3 mol·L-1.
- Vérifier la relation entre la concentration d'un ion et la concentration c de la solution en soluté apporté.
Pour la solution \text{(Cu}^{2+}\text{(aq)} ; \left.2\ \mathrm{Cl}^{-}(\mathrm{aq})\right), de concentration en soluté apporté c, on a \left[\mathrm{Cu}^{2+}\right]=\mathrm{c} et \left[\mathrm{Cl}^{-}\right]=2\ \mathrm{c}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CLoi de Kohlrausch
Pour une solution suffisamment diluée, contenant les ions \text{X}_1\text{(aq)},
\text{X}_2\text{(aq)}, …, et \text{X}_n\text{(aq)}, la conductivité \sigma de la solution s'exprime selon
la loi de Kohlrausch :
\sigma=\lambda_{1} ·\left[\text{X}_{1}\right]+\lambda_{2} \cdot\left[\text{X}_{2}\right]+\ldots+\lambda_{\text{n}} ·\left[\text{X}_{\text{n}}\right]
\displaystyle\sigma=\sum_{i=1}^{n} \lambda_{i}\cdot \left[\text{X}_{i}\right]
\displaystyle\sigma=\sum_{i=1}^{n} \lambda_{i}\cdot \left[\text{X}_{i}\right]
\sigma : conductivité de la solution (S·m-1)
\lambda_1, \lambda_2, … et \lambda_n : conductivités molaires ioniques des espèces ioniques (S·m2·mol-1)
[\text{X}_1], [\text{X}_2], ... et [\text{X}_\text{n}] : concentrations des espèces ioniques (mol·m-3)
\lambda_1, \lambda_2, … et \lambda_n : conductivités molaires ioniques des espèces ioniques (S·m2·mol-1)
[\text{X}_1], [\text{X}_2], ... et [\text{X}_\text{n}] : concentrations des espèces ioniques (mol·m-3)
Les valeurs des conductivités molaires ioniques étant fournies, la mesure de la conductivité permet de déterminer la valeur de la concentration de la solution.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 3Friedrich Kohlrausch
Friedrich Kohlrausch (1840-1910) est un physicien allemand qui s'est intéressé à la conductivité des solutions, mais aussi à la conduction thermique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Analyse spectroscopique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
APrincipe de l'analyse spectroscopique
L'analyse spectroscopique est une technique basée sur l'absorption de certains rayonnements par la substance à analyser.
Un rayonnement incident de longueur d'onde connue traverse la substance étudiée, puis le rayonnement transmis est analysé.
On distingue la spectroscopie UV-visible de la spectroscopie IR, car ces deux techniques utilisent des rayonnements de longueurs d'onde différentes et fournissent des informations différentes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 4Absorbance d'une solution
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BSpectroscopie UV-visible
La spectroscopie UV-visible utilise des rayonnements compris entre 100 nm et 800 nm. Ces rayonnements peuvent être absorbés par les électrons de certaines liaisons moléculaires.
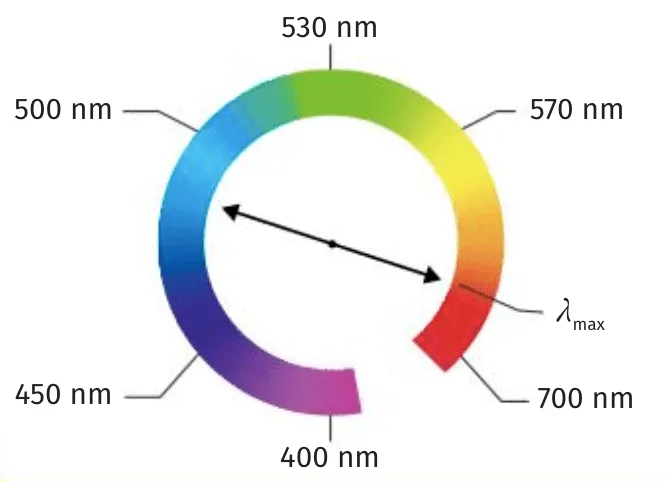
La couleur apparente d'une espèce colorée éclairée sous lumière blanche se déduit de son spectre dans le domaine du visible : il s'agit de la couleur complémentaire du rayonnement pour lequel l'absorbance est maximale.
Pour une longueur d'onde donnée, l'absorbance A_\lambda d'une solution, sans unité, correspond à la somme des absorbances dues à chaque espèce colorée Xi(aq). C'est la loi de Beer-Lambert :
Pour une longueur d'onde donnée, l'absorbance A_\lambda d'une solution, sans unité, correspond à la somme des absorbances dues à chaque espèce colorée Xi(aq). C'est la loi de Beer-Lambert :
A_{\lambda}=\displaystyle\sum_{i=1}^{n} k_{i, \lambda} ·\left [\text{X}_\text{i}\right]
A_{\lambda}=\displaystyle\sum_{i=1}^{n} \varepsilon_{i, \lambda} · l ·\left[\text{X}_\text{i}\right]
A_{\lambda}=\displaystyle\sum_{i=1}^{n} \varepsilon_{i, \lambda} · l ·\left[\text{X}_\text{i}\right]
A_\lambda : absorbance de la solution à la longueur d'onde \lambda
k_{i, \lambda} : coefficient de proportionnalité à la longueur d'onde \lambda (L·mol-1)
\varepsilon_{i, \lambda} : coefficient d'absorption molaire à la longueur d'onde \lambda (L·mol-1·cm-1)
l : épaisseur de la cuve (cm)
[\text{X}_\text{i}] : concentration de l'espèce colorée (mol·L-1)
k_{i, \lambda} : coefficient de proportionnalité à la longueur d'onde \lambda (L·mol-1)
\varepsilon_{i, \lambda} : coefficient d'absorption molaire à la longueur d'onde \lambda (L·mol-1·cm-1)
l : épaisseur de la cuve (cm)
[\text{X}_\text{i}] : concentration de l'espèce colorée (mol·L-1)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 5Couleur et spectre UV du bleu de méthylène
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CSpectroscopie IR
La spectroscopie infrarouge utilise des rayonnements de longueur d'onde comprise entre 2,5 μm et 25 μm (soit 4 000 à 400 cm-1). Ces rayonnements permettent de faire vibrer les liaisons moléculaires.
Sur un spectre IR, on analyse les bandes d'absorption pour identifier des liaisons et en déduire la présence de groupes caractéristiques.
Un spectre IR présente habituellement la transmittance T, grandeur sans unité égale au rapport de l'intensité transmise sur l'intensité incidente, en fonction du nombre d'onde \bar{\nu} :
\bar{\nu}=\frac{1}{\lambda}
\bar{\nu} : nombre d'onde (m-1)
\lambda : longueur d'onde (m)
\lambda : longueur d'onde (m)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Sur un spectre UV-visible, on représente habituellement l'absorbance A en fonction de la longueur d'onde \lambda.
- Sur un spectre IR, on représente habituellement la transmittance T en fonction du nombre d'onde \bar{\nu}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Le symbole \lambda est utilisé pour des grandeurs différentes apparaissant dans ce chapitre :
- la longueur d'onde ;
- la conductivité molaire ionique.
- Le symbole \sigma est couramment employé pour désigner la conductivité et le nombre d'onde. Pour éviter les confusions, on utilise ici \bar{\nu} or pour le nombre d'onde.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3Dosage par étalonnage
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
APrincipe d'un dosage par étalonnage
Un dosage par étalonnage consiste à déterminer la concentration d'une espèce en solution par comparaison avec une gamme de solutions de concentrations connues. Pour réaliser la gamme de solutions étalons, on procède généralement par dilution à partir d'une solution mère, qui contient le même soluté que la solution à analyser.
La concentration de l'espèce testée doit être comprise dans l'intervalle des concentrations utilisées pour l'étalonnage.
En fonction de la substance testée, on peut choisir de mesurer la conductivité, l'absorbance à une longueur d'onde donnée, mais aussi la masse volumique ou d'autres caractéristiques physiques.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Un dosage conductimétrique concerne les solutions ioniques.
- Un dosage spectrophotométrique UV-visible concerne les espèces colorées absorbant dans le visible et les espèces incolores absorbant dans l'UV.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 6Gamme d'étalonnage
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 7Mesure de la conductivité
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application dosage conductimétrique par étalonnage
Application
dosage conductimétrique par étalonnage
Après avoir réalisé une courbe d'étalonnage, on mesure les conductivités \sigma_1 et \sigma_2 de deux solutions S1 et S2.
La valeur \sigma_1 se trouve dans l'intervalle de la gamme étalon : on peut en déduire la concentration c_1 par lecture graphique ou grâce à l'équation de la droite modélisée.
La valeur \sigma_1 se trouve dans l'intervalle de la gamme étalon : on peut en déduire la concentration c_1 par lecture graphique ou grâce à l'équation de la droite modélisée.
La valeur de \sigma_2 se trouve hors de l'intervalle de la gamme d'étalonnage : c_2 ne peut pas être déterminée précisément. Il faut soit diluer la solution S2, soit refaire une gamme d'étalonnage.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La loi de Beer-Lambert est valable également dans le domaine infrarouge. Mais la spectrophotométrie IR n'est généralement pas utilisée pour réaliser des dosages par étalonnage au lycée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BLimites d'un dosage par étalonnage
Les dosages par étalonnage réalisés dans ce chapitre supposent une relation de proportionnalité entre la concentration de l'espèce étudiée et la grandeur mesurée (conductance ou conductivité, absorbance).
Ceci n'est valable que pour des solutions faiblement concentrées en solutés ioniques et à une température donnée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Visionnez la méthode du dosage par étalonnage :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
