Physique-Chimie Terminale Spécialité
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Préparation aux épreuves du Bac
1. Constitution et transformations de la matière
Ch. 1
Modélisation des transformations acide-base
Ch. 2
Analyse physique d'un système chimique
Ch. 3
Méthode de suivi d'un titrage
Ch. 4
Évolution temporelle d'une transformation chimique
Ch. 5
Évolution temporelle d'une transformation nucléaire
BAC
Thème 1
Ch. 6
Évolution spontanée d'un système chimique
Ch. 7
Équilibres acide-base
Ch. 8
Transformations chimiques forcées
Ch. 9
Structure et optimisation en chimie organique
Ch. 10
Stratégies de synthèse
BAC
Thème 1 bis
2. Mouvement et interactions
Ch. 11
Description d'un mouvement
Ch. 12
Mouvement dans un champ uniforme
Ch. 13
Mouvement dans un champ de gravitation
Ch. 14
Modélisation de l'écoulement d'un fluide
BAC
Thème 2
3. Conversions et transferts d'énergie
Ch. 15
Étude d’un système thermodynamique
Ch. 16
Bilans d'énergie thermique
BAC
Thème 3
4. Ondes et signaux
Ch. 17
Propagation des ondes
Ch. 18
Interférences et diffraction
Ch. 19
Lunette astronomique
Ch. 20
Effet photoélectrique et enjeux énergétiques
Ch. 21
Évolutions temporelles dans un circuit capacitif
BAC
Thème 4
Annexes
Ch. 22
Méthode
Chapitre 16
Problèmes à résoudre
Bilans d'énergie thermique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
45Aérogel
✔ VAL : Exploiter un ensemble de mesures
✔ APP : Extraire l'information utile
L'aérogel est un matériau solide extrêmement léger puisque sa composition intègre jusqu'à 99,8 % d'air. C'est aussi le meilleur isolant thermique en raison de sa conductivité thermique λ qui peut tomber à 0,003 W·m‑1·K-1.
En effectuant un bilan d'énergie sur une portion de la surface de l'aérogel en contact avec la fleur, estimer sa température maximum. Seuls les flux de rayonnement et de conduction au travers de l'aérogel seront considérés.


✔ APP : Extraire l'information utile
L'aérogel est un matériau solide extrêmement léger puisque sa composition intègre jusqu'à 99,8 % d'air. C'est aussi le meilleur isolant thermique en raison de sa conductivité thermique λ qui peut tomber à 0,003 W·m‑1·K-1.
En effectuant un bilan d'énergie sur une portion de la surface de l'aérogel en contact avec la fleur, estimer sa température maximum. Seuls les flux de rayonnement et de conduction au travers de l'aérogel seront considérés.


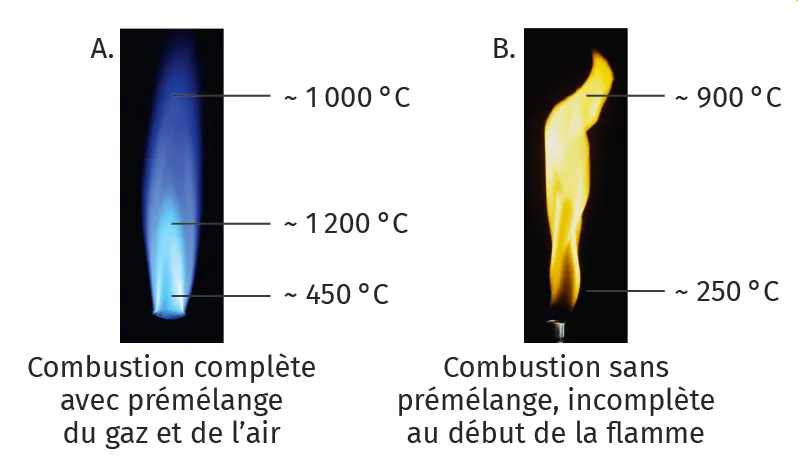
Doc. 1
Températures de flamme

Doc. 2
Résolution graphique
Pour résoudre une équation du quatrième degré de la forme a · x^{4}+b · x^{3}+c · x^{2}+d · x+e=0, on peut utiliser un tableur‑grapheur pour tracer la fonction f(x) = a · x^{4}+b · x^{3}+c · x^{2}+d · x+e=0.
Sa résolution passe par la recherche des valeurs de x pour lesquelles f(x) = 0.
Le nombre de solutions à considérer peut être réduit grâce à des considérations physiques.
Sa résolution passe par la recherche des valeurs de x pour lesquelles f(x) = 0.
Le nombre de solutions à considérer peut être réduit grâce à des considérations physiques.
Données
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retour sur la problématique du chapitre
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
46Tuile de navette spatiale
✔
APP : Faire des prévisions à l'aide d'un modèle
✔ VAL : Évaluer et connaître des ordres de grandeur
Les tuiles des boucliers thermiques des navettes spatiales sont conçues pour protéger la structure interne des fortes chaleurs causées par la pénétration dans l'atmosphère.
Alors que la surface des tuiles peut atteindre près de 1 650 °C, la structure interne en aluminium ne doit pas dépasser les 180 °C. La conductivité thermique est donc particulièrement faible (λ = 0{,}01 W·m-1·K-1) et l'épaisseur atteint 13 cm pour protéger les parties les plus exposées. 1. Calculer le flux thermique rayonné par une surface de 1 m2 de tuiles de navette spatiale.
2. Calculer le flux thermique qui peut passer à travers 1 m2 du bouclier par conduction.
✔ VAL : Évaluer et connaître des ordres de grandeur
Les tuiles des boucliers thermiques des navettes spatiales sont conçues pour protéger la structure interne des fortes chaleurs causées par la pénétration dans l'atmosphère.
Alors que la surface des tuiles peut atteindre près de 1 650 °C, la structure interne en aluminium ne doit pas dépasser les 180 °C. La conductivité thermique est donc particulièrement faible (λ = 0{,}01 W·m-1·K-1) et l'épaisseur atteint 13 cm pour protéger les parties les plus exposées. 1. Calculer le flux thermique rayonné par une surface de 1 m2 de tuiles de navette spatiale.
2. Calculer le flux thermique qui peut passer à travers 1 m2 du bouclier par conduction.
3. Comparer les deux valeurs et expliquer pourquoi la tuile peut être touchée à main nue.


Expression de la résistance thermique de conduction : R_{\mathrm{th}}=\frac{e}{\lambda · S}
Expression de la loi de Stefan‑Boltzmann : \varphi=\sigma \cdot T^{4}
Constante de Stefan‑Boltzmann : σ = 5{,}67 \times 10^{-8} W·m-2·K-4
Doc.
Tuile de navette spatiale


Données
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
