Bilans d'énergie thermique

Les échanges d'énergie par transfert thermique peuvent s'effectuer suivant trois modes d'un système à un autre :

• la conduction : l'énergie se propage dans un milieu matériel grâce à l'agitation thermique des particules, qui se transmet de proche en proche ;
• la convection : l'énergie est transportée par les déplacements du fluide lui-même. Elle peut être naturelle si seules la dilatation et la gravité déplacent le fluide ou forcée si le fluide est poussé à se déplacer ;
• le rayonnement : tout corps porté à une certaine température émet des ondes électromagnétiques qui peuvent augmenter l'énergie interne d'autres corps à distance.

• Attention à ne pas confondre t le temps et T la température.
• Utiliser \theta pour les températures exprimées en degré Celsius (°C).
• Attention au signe du flux : comme pour le transfert thermique, il est positif quand le système le reçoit.

Le flux thermique \phi correspond au transfert thermique échangé par un système par unité de temps avec l'extérieur :
Le flux thermique est proportionnel à l'écart de température entre le système étudié et l'extérieur :
La résistance thermique est une grandeur qui dépend de l'épaisseur de la paroi, de la surface d'échange, mais également de la nature du matériau considéré.

Exemple :
Pour 1 m² d'aérogel, la résistance thermique est de l'ordre de 0,6 K·W^-1 pour une épaisseur de 1 cm. Une paroi en brique de même épaisseur possède une résistance de 12 mK·W^-1. En acier, cette valeur atteint 0,2 mK·W^-1.

Le flux thermique échangé à travers une paroi est proportionnel à l'écart de température entre les deux côtés.

Lorsqu'un fluide est au contact d'une paroi fine thermostatée, le flux thermique conducto-convectif s'exprime en fonction de l'écart entre la température du système T et celle de la paroi.

• Il faut faire attention aux valeurs de h, car chaque cas étudié a son propre coefficient h. Il dépend du mouvement du fluide, de la turbulence, de la rugosité et de la géométrie de la paroi.
  


• Un écart de températures exprimées en degré Celsius (°C) est égal à l'écart de ces mêmes températures exprimées en kelvin (K).

Tout corps à température T émet un rayonnement électromagnétique. La loi de Stefan-Boltzmann permet d'établir une relation entre le flux thermique surfacique émis \varphi et la température T :

Tout corps émet un rayonnement. Plus la température est élevée, plus la longueur du maximum d'intensité émise est déplacée vers les courtes longueurs d'onde.

Le rayonnement solaire parvenant jusqu'à la Terre est sa source principale d'énergie thermique. Comme la température moyenne de la surface de la Terre est stable au fil des ans, cela signifie que la surface reçoit en moyenne autant d'énergie qu'elle en émet vers l'espace par son propre rayonnement.


La Terre reçoit un rayonnement solaire dont le flux thermique surfacique moyen est de l'ordre de \varphi_{\mathrm{s}}=340 W·m^-2. Environ a=30 % de ce rayonnement est réfléchi sans être absorbé par l'atmosphère : cette proportion est appelée albédo.

Plus l'albédo est élevé, plus le rayonnement solaire est réfléchi et moins la surface de la Terre reçoit d'énergie thermique. Si une partie du rayonnement émis par la Terre n'était pas absorbée par l'atmosphère (principalement dans le domaine des infrarouges), la température à la surface serait d'environ -18 °C. Cette absorption essentiellement due à la présence d'eau \mathrm{H_{2}O} et de dioxyde de carbone \mathrm{CO_{2}} dans l'atmosphère s'appelle l'effet de serre.

Cet effet de serre naturel permet à la surface de la Terre de récupérer une partie de l'énergie qu'elle rayonne, contribuant ainsi à son réchauffement jusqu'à une température moyenne de 15 °C.

Retrouvez une

vidéo explicative sur l'albédo.

Ne pas oublier que la puissance solaire reçue au niveau du sol est une moyenne sur toute la surface de la Terre sur 24 h.

Avec les développements industriels de ces deux derniers siècles et la surconsommation, l'humanité a libéré dans l'atmosphère une quantité importante de gaz à effet de serre. Ces gaz contribuent au réchauffement global et au dérèglement climatique.

Lorsqu'un système incompressible de température T échange uniquement de l'énergie avec une paroi thermostatée à une température T_{\text {ext }}, le premier principe de la thermodynamique s'écrit :
En dérivant par rapport au temps cette égalité, on peut établir que :
La dérivée de l'énergie interne U par rapport au temps t est égale au flux thermique. Au contact d'un thermostat et sans changement d'état du système, tout peut s'exprimer en fonction de la seule variable T, la température du système. En utilisant la capacité thermique massique c : On obtient :
De même, le flux thermique, si on ne tient compte que du transfert conducto-convectif, s'exprime avec la loi de Newton : Ainsi, l'équation devient :
Cette équation est une équation différentielle. La variation de température d'un système au cours du temps est proportionnelle à la différence de température entre le système et le thermostat.

Attention au signe du flux thermique  \phi. Ici, si la température du thermostat est plus forte, le flux est positif, car le système reçoit de l'énergie.

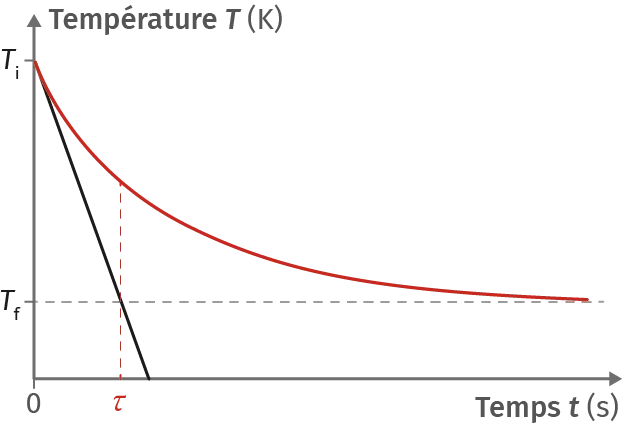
Au terme de 5 \tau, la variation de température a atteint 99 % de la valeur attendue \theta_{i}-\theta_{f} .

L'équation différentielle précédente peut s'écrire sous la forme :
La grandeur \tau=\frac{m \cdot c}{h \cdot S} désigne le temps caractéristique d'évolution de la température. Dans le cas où \tau est indépendant de la température T, les solutions de cette équation différentielle sont de la forme
T(t)=A \cdot \exp \left(-\frac{t}{\tau}\right)+B
Si on note T_{i} la température initiale du système étudié et T_{\text {ext }} celle du thermostat, alors la température T en fonction du temps t a pour expression :

Pour vérifier que l'expression de \tau est correcte, il faut se souvenir que la masse et la capacité thermique augmentent \tau (le système met plus de temps à se réchauffer). Au contraire, tout ce qui augmente le flux thermique diminue  \tau.