Mathématiques 1re Techno
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Analyse
Ch. 1
Suites
Ch. 2
Fonctions
Ch. 3
Dérivation
Partie 2 : Statistiques et probabilités
Ch. 4
Fréquences conditionnelles et probabilités conditionnelles
Ch. 5
Variables aléatoires
Automatismes
Partie 3 : Géométrie
Ch. 6
Trigonométrie
Ch. 7
Produit scalaire
Ch. 8
Nombres complexes
Partie 4 : Analyse
Ch. 9
Compléments sur la dérivation
Ch. 10
Primitives
Révisions Genially
Chapitre 4
L'essentiel
Fréquences conditionnelles et probabilités conditionnelles
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Fiche méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
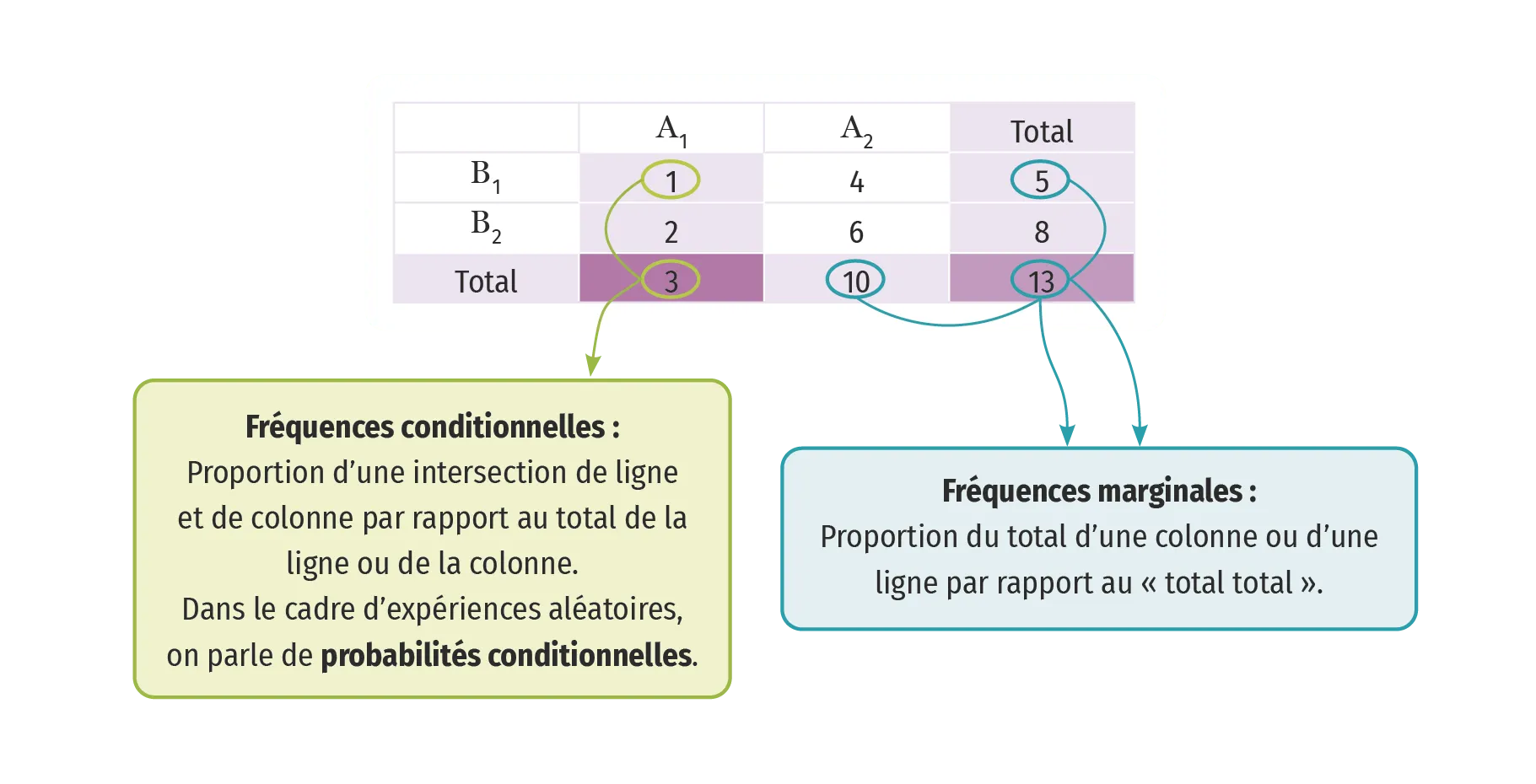
1Calculer des fréquences marginales (\bf{A} dans \bf{E})
- On commence par déterminer les effectifs de \text{A} et de \text{E}.
- La fréquence marginale de \text{A} dans \text{E} est :
f=\frac{\text { Effectif total de } \mathrm{A}}{\text { Effectif total } \mathrm{de}\:\mathrm{E}}=\frac{\operatorname{Card}(\mathrm{A})}{\operatorname{Card}(\mathrm{E})}.
| \text{A} | \overline{\text{A}} | Total | |
|---|---|---|---|
| \text{B} | 20 | 15 | 35 |
| \overline{\text{B}} | 12 | 53 | 65 |
| Total | 32 | 68 | 100 |
f=\frac{32}{100}=0,32
Auto‑évaluation et
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Calculer la fréquence conditionnelle de \bf{A} parmi \bf{B}
- Pour calculer la fréquence conditionnelle de \text{A} relativement à \text{B}, il faut déterminer l'effectif de \text{A} \cap \text{B} et l'effectif total de \text{B}.
- La fréquence conditionnelle de \text{A} relativement à \text{B} est :
f=\frac{\text { Effectif total de } \text{A} \cap \text{B}}{\text { Effectif total de } \text{B}}=\frac{\operatorname{Card}(\text{A} \cap \text{B})}{\operatorname{Card}(\text{B})} \text { . }
| \text{A} | \overline{\text{A}} | Total | |
|---|---|---|---|
| \text{B} | 20 | 15 | 35 |
| \overline{\text{B}} | 12 | 53 | 65 |
f=\frac{20}{35}
Auto‑évaluation et
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3Compléter un tableau croisé d'effectifs
- Compléter la dernière case d'une ligne ou d'une colonne en procédant par additions et soustractions.
- Utiliser les fréquences conditionnelles lorsqu'il manque plus d'une case sur une ligne ou sur une colonne : l'effectif de la case située à l'intersection de la colonne \text{A} et de la ligne \text{B} est égal à l'effectif de B multiplié par la fréquence conditionnelle de \text{A} relativement à \text{B}.
Auto‑évaluation et
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4Calculer des probabilités conditionnelles
- Utiliser le tableau croisé d'effectifs.
\text{A} \overline{\text{A}} Total \text{B} 20 15 35 \overline{\text{B}} 12 53 65
\text{P}_\text{B}(\text{A})=\frac{20}{35} - Utiliser la formule \mathrm{P}_{\mathrm{B}}(\mathrm{A})=\frac{\operatorname{Card}(\mathrm{A} \cap \mathrm{B})}{\operatorname{Card}(\mathrm{B})}.
Auto‑évaluation et
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Carte mentale
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille