Mathématiques 3e - 2021
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Nombres et calculs
Ch. 1
Nombres entiers
Ch. 2
Calcul numérique
Ch. 3
Calcul littéral
Ch. 4
Équations
Partie 2 : Organisation et gestion de données, fonctions
Ch. 5
Notion de fonction
Ch. 6
Fonctions affines
Ch. 7
Situations de proportionnalité
Ch. 8
Statistiques
Ch. 9
Probabilités
Partie 3 : Espace et géométrie
Ch. 10
Théorème de Thalès et triangles semblables
Ch. 11
Trigonométrie dans le triangle rectangle
Ch. 12
Transformations dans le plan et leurs effets
Ch. 13
Géométrie dans l'espace
Partie 4 : Mesures et grandeurs
Ch. 14
Mesures et grandeurs
Annexes
Scratch
Dossier brevet
Rappels, Index, Compétences
Révisions Genially
Calcul littéral
Plan de travail
Plan de travail
Approfondissement
Exclusivité numérique
Brevet
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1D'après brevet, Métropole, juin 2018
Durée : 15 minVoici un programme de calcul.
\boxed{
\begin{array} { r|l } 1 & \text{Choisir un nombre} \\
2 & \text{Multiplier ce nombre par 4} \\
3 & \text{Ajouter 8} \\
4 & \text{Multiplier le résultat par 2}
\end{array}
}
1.
Vérifier que si l'on choisit le nombre -1, ce programme donne 8 comme résultat final.
L'expression \mathrm{A}=2(4 x+8) donne le résultat du programme de calcul précédent pour un nombre x donné. On pose {\mathrm{B}=(4+x)^{2}-x^{2}}.
Prouver que les expressions \text{A} et \text{B} sont égales pour toutes les valeurs de x.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2D'après brevet, Asie, juin 2017
Durée : 20 min
Gaspard réalise des motifs avec des carreaux de mosaïque blancs et bleus. Il forme un carré avec des carreaux bleus puis le borde avec des carreaux blancs de la manière suivante :
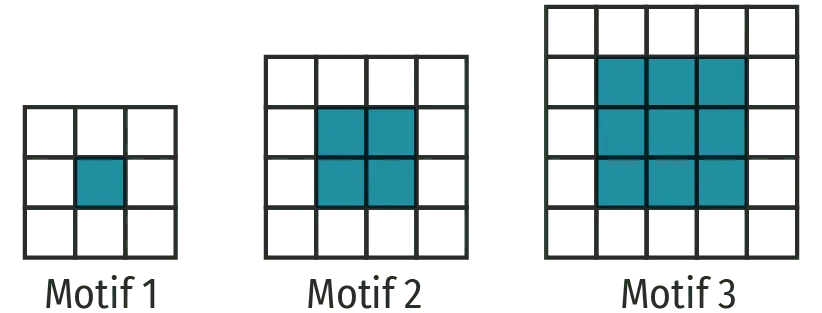
Gaspard réalise des motifs avec des carreaux de mosaïque blancs et bleus. Il forme un carré avec des carreaux bleus puis le borde avec des carreaux blancs de la manière suivante :
1.
Combien de carreaux blancs Gaspard va-t-il utiliser pour border la partie bleue du motif 4 (un carré ayant 4 carreaux bleus de côté) ?
2. a.
Justifier que Gaspard peut réaliser un motif de ce type en utilisant exactement 144 carreaux bleus.
b.
Combien de carreaux blancs utilisera-t-il alors pour border le carré bleu obtenu ?
3.
On appelle « motif n », le motif pour lequel on borde un carré de côté n carreaux bleus.
Trois élèves ont proposé chacun une expression pour calculer le nombre de carreaux blancs nécessaires pour réaliser le « motif n ».
Trois élèves ont proposé chacun une expression pour calculer le nombre de carreaux blancs nécessaires pour réaliser le « motif n ».
- Expression n°1 : 2 \times n+2 \times(n+2)
- Expression n°2 : 4 \times(n+2)
- Expression n°3 : 4 \times(n+2)-4
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
82D'après brevet, Asie, juin 2019
Durée : 20 min
Nina et Claire ont chacune un programme de calcul.
Nina et Claire ont chacune un programme de calcul.
\boxed{
\begin{array} { r|l }
& \rightarrow \text{Programme de Nina}\\
1 & \text{Choisir un nombre} \\
2 & \text{Soustraire 1} \\
3 & \text{Multiplier le résultat par –2} \\
4 & \text{Ajouter 2} \\
\end{array}
}
\boxed{
\begin{array} { r|l }
& \rightarrow \text{Programme de Claire}\\
1 & \text{Choisir un nombre} \\
2 & \text{Multiplier ce nombre par} -\frac{1}{2} \\
3 & \text{Ajouter 1 au résultat}
\end{array}
}
1.
Montrer que si les deux filles choisissent 1 comme nombre de départ, Nina obtiendra un résultat final quatre fois plus grand que celui de Claire.
2.
Quel nombre de départ Nina doit-elle choisir pour obtenir 0 à la fin ?
3.
Nina dit à Claire : « Si on choisit le même nombre de départ, mon résultat sera toujours quatre fois plus grand que le tien. ». A-t-elle raison ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
