Enseignement mathématique 1re

Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Exercices rituels et automatismes
Exercices rituels
Automatismes
Partie 1 - Information chiffrée
Ch. 1
Analyse de l'information chiffrée
Partie 2 - Probabilités
Ch. 2
De la statistique aux probabilités
Partie 3 - Phénomènes d’évolution
Ch. 3
Croissance linéaire
Ch. 4
Croissance exponentielle
Partie 4 - Dérivation
Ch. 5
Variations instantanées
Ch. 6
Variations globales
GeoGebra
Chapitre 5
Activité A
Tangente à une courbe en un point
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Comprendre ce qu'est la tangente à une courbe en un point en utilisant des fonctionnalités de GeoGebra
Comprendre ce qu'est la tangente à une courbe en un point en utilisant des fonctionnalités de GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
On considère la fonction f définie sur \mathbb{R} par f(x)=-x^{3}+3 x^{2}-1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions
1
a. À l'aide de GeoGebra, construire la courbe représentative \mathcal{C}_f de la fonction f. Ne pas hésiter à modifier l'échelle pour plus de lisibilité.b. Placer sur \mathcal{C}_f le point \mathrm{A} d'abscisse 1 et le point \mathrm{B} d'abscisse 2.
2
a. Construire un point \mathrm{C} quelconque distinct de \mathrm{A} et \mathrm{B} sur \mathcal{C}_f.
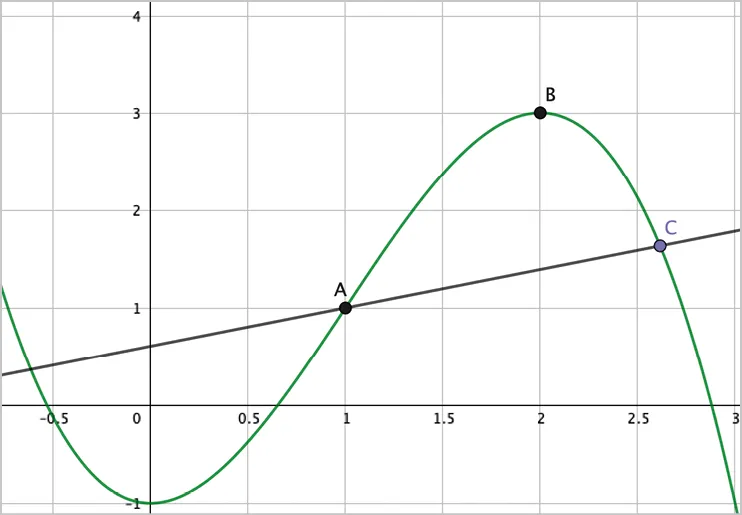
c. Que se passe-t-il lorsque les points \mathrm{A} et \mathrm{C} sont confondus ? Comment l'expliquer ?
3
a. À l'aide de l'outil « Tangentes » de GeoGebra, tracer la tangente à la courbe représentative de f passant par le point \mathrm{A}.

Aide
Après avoir sélectionné l'outil, il suffit de cliquer n'importe où sur la courbe puis sur le point \mathrm{A}.
b. Où faut-il placer le point \mathrm{C} pour que la droite \mathrm{(AC)} soit presque confondue avec la tangente à \mathcal{C}_f en \mathrm{A} ?
c. Zoomer sur le point \mathrm{A}. Que peut-on dire de la courbe représentative de f et de sa tangente en \mathrm{A} au fur et à mesure que le zoom devient plus important ?
4
a. Tracer la tangente à la courbe représentative de f passant par \mathrm{B}.
Comment peut-on décrire cette droite ?b. Que peut-on dire de la tangente à \mathcal{C}_f en \mathrm{B} et de la courbe représentative de f au fur et à mesure que l'on zoome sur le point \mathrm{B} ?
5
a. Construire le point \mathrm{D} d'abscisse -1 sur la courbe représentative de f.b. Construire la tangente à la courbe représentative de f passant par \mathrm{D}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Bilan
Lorsque \mathrm{A} et \mathrm{C} sont deux points de la courbe \mathcal{C}_f d'une fonction f, dans quelle situation peut-on dire que la droite \mathrm{(AC)} est très proche de la tangente à \mathcal{C}_f au point \mathrm{A} ? Donner une définition intuitive de cette tangente.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
