Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonom étriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 7
TP / TICE 1
Approximation de \pi par la méthode d'Archimède
17 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
On souhaite connaître le plus précisément possible la valeur de \pi.
Pour cela, on va utiliser la méthode d'Archimède qui consiste à encadrer la circonférence d'un cercle de rayon 1 par des polygones réguliers inscrits et circonscrits ayant de plus en plus de côtés.
Le zoom est accessible dans la version Premium.
Le zoom est accessible dans la version Premium.
Questions préliminaires :
On note \mathrm{P}_{n} la valeur du périmètre du polygone régulier intérieur à n côtés et \mathrm{P}_{n}^{\prime} celle du polygone régulier extérieur à n côtés.
On note \mathrm{P}_{n} la valeur du périmètre du polygone régulier intérieur à n côtés et \mathrm{P}_{n}^{\prime} celle du polygone régulier extérieur à n côtés.
1. À l'aide de la figure, justifier que \mathrm{P}_{6}=6.
2. En sachant que \tan (30)=\dfrac{\sqrt{3}}{3}, justifier que \mathrm{P}_{6}^{\prime}=4 \sqrt{3}.
3. En déduire une première approximation de \pi. On admet pour la suite que \mathrm{P}_{n}=2 \times n \times \sin \left(\dfrac{180}{n}\right) et \mathrm{P}_{n}^{\prime}=2 \times n \times \tan \left(\dfrac{180}{n}\right).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Donner une approximation de \pi avec
la précision souhaitée à l'aide d'une des
deux méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1Tableur
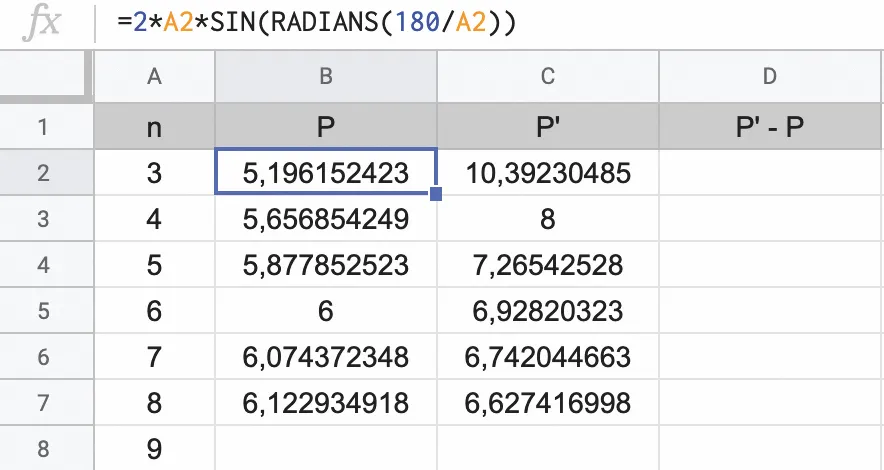
1. Créer une feuille de calcul permettant de calculer
\text{P} et \text{P}' en fonction de n.
Remarque : Les fonctions trigonométriques du tableur attendent des angles en radian donc, si on veut calculer la valeur du cosinus de 130°, on écrira : =cos(RADIANS(130)).
Remarque : Les fonctions trigonométriques du tableur attendent des angles en radian donc, si on veut calculer la valeur du cosinus de 130°, on écrira : =cos(RADIANS(130)).
Le zoom est accessible dans la version Premium.
2.
Dans la colonne D, afficher la différence entre \text{P}'
et \text{P.}
3. Quelle valeur faut-il donner à n pour avoir un encadrement de \pi d'amplitude 10^{-1}\: ?
Quelle serait alors une approximation de \pi ?
4. Quelle valeur faut-il donner à n pour avoir un encadrement de \pi d'amplitude 10^{-2}\: ? Quelle serait alors une approximation de \pi ?
3. Quelle valeur faut-il donner à n pour avoir un encadrement de \pi d'amplitude 10^{-1}\: ?
Quelle serait alors une approximation de \pi ?
4. Quelle valeur faut-il donner à n pour avoir un encadrement de \pi d'amplitude 10^{-2}\: ? Quelle serait alors une approximation de \pi ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Python
On souhaite créer un programme permettant de calculer une approximation de \pi avec une
précision p donnée. Dans l'algorithme suivant, on note n le nombre de côtés des deux polygones et \text{P1} et \text{P2} correspondent respectivement aux
périmètres \mathrm{P}_{n} et \text{P}_{n}^{\prime}.
1. Reproduire et compléter cet algorithme.
2. Expliquer la condition d'arrêt de la boucle Tant que.
\boxed{
\begin{array} {c|l }
1&\text { p } \leftarrow \text { 1 } \\
2&\text { n } \leftarrow \text { 6 } \\
3&\text { P1 } \leftarrow \text { ... } \\
4&\text { P2 } \leftarrow \text { ... } \\
5&\text { A } \leftarrow \text { P1 / 2 } \\
6&\text { B } \leftarrow \text { P2 / 2 } \\
7&\text { Tant que } \text{(B-A)} > 10^{-\text{p}} : \\
8&\quad \text { n } \leftarrow \text { n+1 } \\
9&\quad \text { A } \leftarrow \text { ... } \\
10&\quad \text { B } \leftarrow \text { ... } \\
11&\text {Fin Tant que}
\end{array}
}
1. Reproduire et compléter cet algorithme.
2. Expliquer la condition d'arrêt de la boucle Tant que.
3. Programmer cet algorithme avec Python afin d'obtenir un encadrement de \pi avec la précision p donnée ainsi que le nombre de côtés correspondant. Choisir p = 1 pour commencer puis p = 2.
On pensera à utiliser la fonction radians pour manipuler des angles en radian avec Python.
On pensera à utiliser la fonction radians pour manipuler des angles en radian avec Python.
from math import *
Cliquez pour accéder à la correction
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah