Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonom étriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 7
TP / TICE 2
Propriétés des angles associés
16 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Lorsque l'on connaît les valeurs du cosinus et du sinus d'un angle, on souhaite savoir comment trouver, sans utiliser la calculatrice, la valeur du cosinus et du sinus de plusieurs angles qui lui sont associés : opposé, supplémentaire, antisupplémentaire, complémentaire et anticomplémentaire.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Déterminer des cosinus et des sinus
de certaines valeurs en utilisant les
valeurs particulières à l'aide d'une
des deux méthodes.
Objectif
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
TABLEUR
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. Recopier la feuille de calcul ci-dessous et entrer dans les colonnes C et D une formule permettant de calculer les valeurs de \cos (x) et \sin (x).
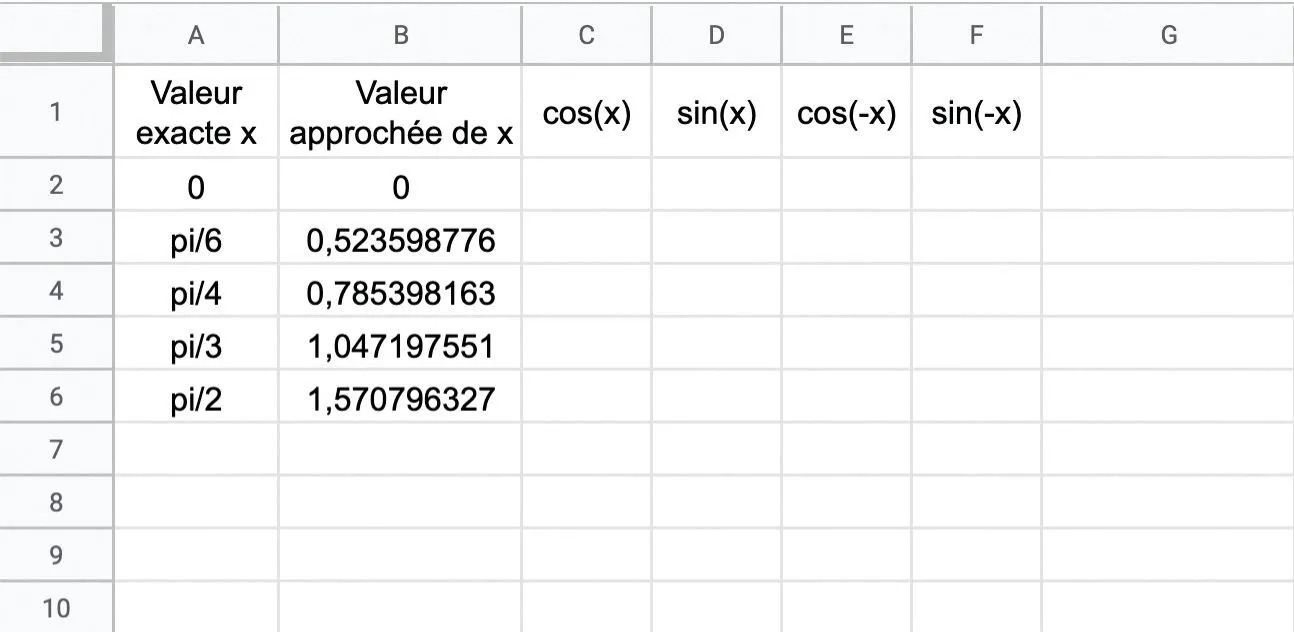
2. Dans les colonnes E et F, écrire une formule permettant de calculer \cos (-x) et \sin (-x). En déduire la relation pour les angles opposés c'est-à-dire entre \cos (-x), \sin (-x) et \cos (x), \sin (x).
3. Procéder de même avec l'angle supplémentaire \pi-x, l'angle antisupplémentaire \pi+x, l'angle complémentaire \dfrac{\pi}{2}-x et l'angle anticomplémentaire \dfrac{\pi}{2}+x.
4. Retrouver ces résultats à partir du cercle trigonométrique.
Le zoom est accessible dans la version Premium.
2. Dans les colonnes E et F, écrire une formule permettant de calculer \cos (-x) et \sin (-x). En déduire la relation pour les angles opposés c'est-à-dire entre \cos (-x), \sin (-x) et \cos (x), \sin (x).
3. Procéder de même avec l'angle supplémentaire \pi-x, l'angle antisupplémentaire \pi+x, l'angle complémentaire \dfrac{\pi}{2}-x et l'angle anticomplémentaire \dfrac{\pi}{2}+x.
4. Retrouver ces résultats à partir du cercle trigonométrique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
GEOGEBRA
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
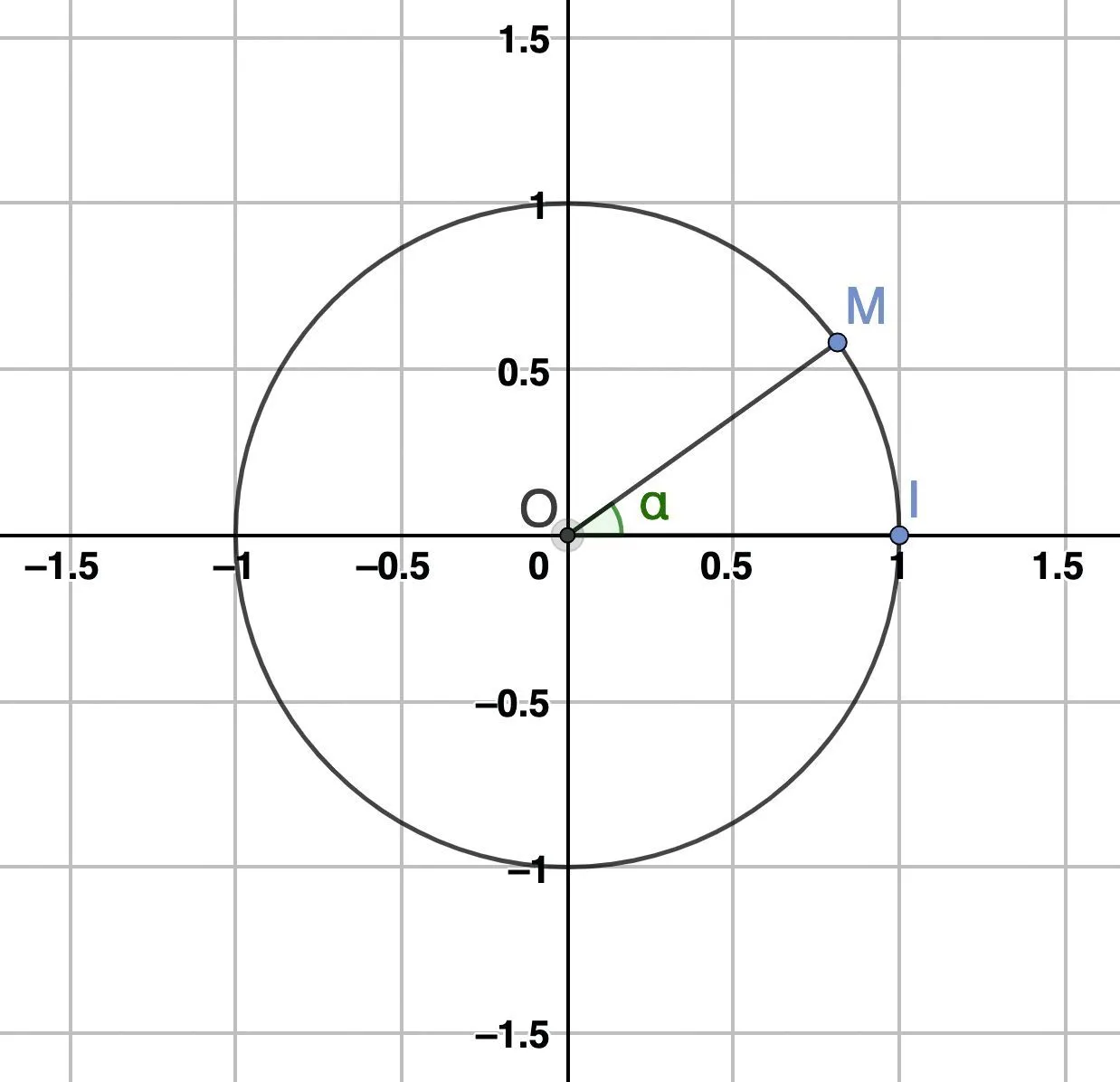
1. Effectuer les étapes suivantes :
2. a. Dans la barre saisie, entrer r=\cos (-\alpha) puis s=\sin (-\alpha).
b. Faire bouger le point \text{M} sur le cercle.
c. Que remarque-t-on quant aux valeurs de p, q, r et s\:? Que peut-on en déduire ?
3. Procéder de même avec l'angle supplémentaire \pi-\alpha et l'angle antisupplémentaire \pi+\alpha.
4. Même question avec l'angle complémentaire \dfrac{\pi}{2}-\alpha et l'angle anticomplémentaire \dfrac{\pi}{2}+\alpha.
5. Quelles transformations géométriques permettent de justifier ces résultats ?
- dans les options avancées, choisir « Radian » comme unité d'angles ;
- tracer le cercle trigonométrique dans le repère (\text{O ; I , J}) puis placer un point \text{M} sur ce cercle ;
- faire apparaître l'angle \alpha=\widehat{\mathrm{IOM}}\::
- dans la barre de saisie, entrer p=\cos (\alpha) puis q=\sin (\alpha).
Aide
Le clavier de GeoGebra permet d'insérer des
caractères spéciaux comme \alpha .
Le zoom est accessible dans la version Premium.
2. a. Dans la barre saisie, entrer r=\cos (-\alpha) puis s=\sin (-\alpha).
b. Faire bouger le point \text{M} sur le cercle.
c. Que remarque-t-on quant aux valeurs de p, q, r et s\:? Que peut-on en déduire ?
3. Procéder de même avec l'angle supplémentaire \pi-\alpha et l'angle antisupplémentaire \pi+\alpha.
4. Même question avec l'angle complémentaire \dfrac{\pi}{2}-\alpha et l'angle anticomplémentaire \dfrac{\pi}{2}+\alpha.
5. Quelles transformations géométriques permettent de justifier ces résultats ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
GeoGebra
GeoGebra
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah