Travailler autrement
Python
Tracer un vecteur variation de vitesse
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
A.Afficher le vecteur vitesse d'un point matériel sur la trajectoire
Objectif de l'activité : on utilise le script ci-dessous pour afficher la trajectoire d'un point mobile et le vecteur vitesse moyenne de ce point à une date donnée.
1. Rappeler la formule du vecteur vitesse au point \text{M}_3, approximé au vecteur vitesse moyenne entre \text{M}_2 et \text{M}_3. Quelle différence observe-t-on dans le calcul des coordonnées du vecteur vitesse dans le script ?
Analyse du problème
Le vecteur vitesse moyenne est colinéaire au vecteur déplacement avec un facteur \dfrac{1}{\Delta t}.
Dans cette activité, on souhaite uniquement observer la direction du vecteur vitesse et du vecteur variation de vitesse, il n'est donc pas nécessaire de prendre en compte ce facteur multiplicatif.
Les coordonnées doivent être rentrées dans des listes pour que la fonction aille chercher les coordonnées x_\text{i} et x_\text{i+1} ainsi que y_\text{i} et y_\text{i+1}.
1. Rappeler la formule du vecteur vitesse au point \text{M}_3, approximé au vecteur vitesse moyenne entre \text{M}_2 et \text{M}_3. Quelle différence observe-t-on dans le calcul des coordonnées du vecteur vitesse dans le script ?
import matplotlib.pyplot as plt
x=[]
y=[]
plt.plot(x,y,'r+',ms=20.) # tracé des points, ms détermine la taille des marqueurs.
plt.axis('equal')
def vitesse(x,y,i) :
# x et y sont des listes contenant les coordonnées, i le numéro du point
# dont on affiche la vitesse
plt.arrow(x[i],y[i],(x[i+1]-x[i]),(y[i+1]-y[i]) , shape='full', lw=1,
length_includes_head=True, rasterized=True, color='c', head_width=.05,fc='c')
vitesse(x,y,4) # appel de la fonction, ici au point 5 (4+1).
plt.show() # affichage du tracé.Analyse du problème
Le vecteur vitesse moyenne est colinéaire au vecteur déplacement avec un facteur \dfrac{1}{\Delta t}.
Dans cette activité, on souhaite uniquement observer la direction du vecteur vitesse et du vecteur variation de vitesse, il n'est donc pas nécessaire de prendre en compte ce facteur multiplicatif.
Les coordonnées doivent être rentrées dans des listes pour que la fonction aille chercher les coordonnées x_\text{i} et x_\text{i+1} ainsi que y_\text{i} et y_\text{i+1}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
B.Tracer le vecteur variation de vitesse
Objectif de l'activité : À partir du script précédent, ajouter les lignes de code permettant de faire apparaître le vecteur vitesse moyenne au point M_{\text{i}+1}\: \vec v_{\text{i}+1}, puis le vecteur variation de vitesse \Delta \vec v_\text{i} = \vec v_{\text{i}+1} - \vec v_\text{i}.
Analyse du problème
On n'effectue pas les calculs complets du vecteur variation de vitesse. On se contente de faire la différence des vecteurs déplacement afin de pouvoir trouver la direction du vecteur variation de vitesse.
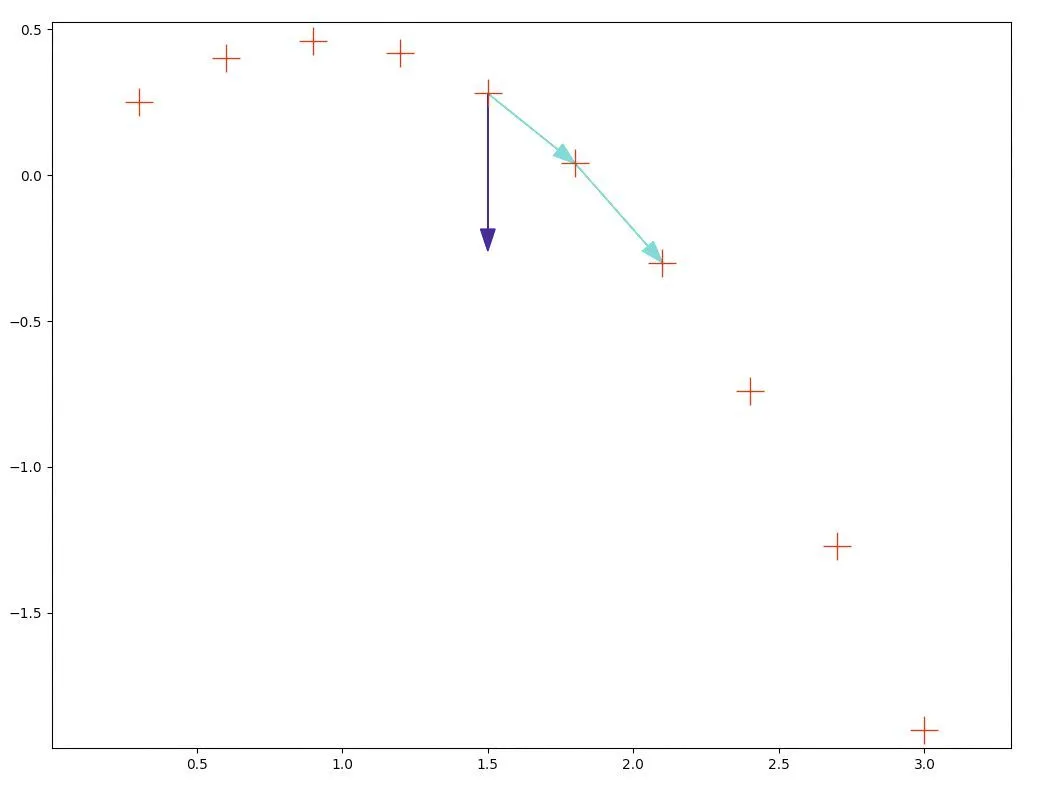
Mise en œuvre : Effectuer le tracé du vecteur variation de vitesse \Delta \vec v_\text{i} pour plusieurs points de la trajectoire suivante qui correspond au mouvement d'une balle à la surface de la Terre.
\begin{array}{l}{\text{M}_{1}\left(\begin{array}{l}{0} \\ {0}\end{array}\right) ; \text{M}_{2}\left(\begin{array}{c}{0\text{,}3} \\ {0\text{,}25}\end{array}\right) ; \text{M}_{3}\left(\begin{array}{c}{0\text{,}6} \\ {0\text{,}40}\end{array}\right) ; \text{M}_{4}\left(\begin{array}{c}{0\text{,}9} \\ {0\text{,}46}\end{array}\right) ; \text{M}_{5}\left(\begin{array}{c}{1\text{,}2} \\ {0\text{,}42}\end{array}\right)} \\ {\text{M}_{6}\left(\begin{array}{c}{1\text{,}5} \\ {0\text{,}28}\end{array}\right) ; \text{M}_{7}\left(\begin{array}{c}{1\text{,}8} \\ {0\text{,}04}\end{array}\right) ; \text{M}_{8}\left(\begin{array}{c}{2\text{,}1} \\ {-0\text{,}30}\end{array}\right) ; \text{M}_{9}\left(\begin{array}{c}{2\text{,}4} \\ {-0\text{,}74}\end{array}\right)}\end{array}
Analyse du problème
On n'effectue pas les calculs complets du vecteur variation de vitesse. On se contente de faire la différence des vecteurs déplacement afin de pouvoir trouver la direction du vecteur variation de vitesse.
Mise en œuvre : Effectuer le tracé du vecteur variation de vitesse \Delta \vec v_\text{i} pour plusieurs points de la trajectoire suivante qui correspond au mouvement d'une balle à la surface de la Terre.
\begin{array}{l}{\text{M}_{1}\left(\begin{array}{l}{0} \\ {0}\end{array}\right) ; \text{M}_{2}\left(\begin{array}{c}{0\text{,}3} \\ {0\text{,}25}\end{array}\right) ; \text{M}_{3}\left(\begin{array}{c}{0\text{,}6} \\ {0\text{,}40}\end{array}\right) ; \text{M}_{4}\left(\begin{array}{c}{0\text{,}9} \\ {0\text{,}46}\end{array}\right) ; \text{M}_{5}\left(\begin{array}{c}{1\text{,}2} \\ {0\text{,}42}\end{array}\right)} \\ {\text{M}_{6}\left(\begin{array}{c}{1\text{,}5} \\ {0\text{,}28}\end{array}\right) ; \text{M}_{7}\left(\begin{array}{c}{1\text{,}8} \\ {0\text{,}04}\end{array}\right) ; \text{M}_{8}\left(\begin{array}{c}{2\text{,}1} \\ {-0\text{,}30}\end{array}\right) ; \text{M}_{9}\left(\begin{array}{c}{2\text{,}4} \\ {-0\text{,}74}\end{array}\right)}\end{array}

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Entraînez-vous à programmer en langage Python sur
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille


