Notion de vecteur

1

Calculer avec des nombres relatifs

Calculer les expressions suivantes.

1. \text{A}=(-5)+8+(-3)-5-(-10)

2. \mathrm{B}=5+(-8)+3-(-5)-10

3. \mathrm{C}=x-y+z \text { et } \mathrm{D}=-x+y+3 z pour x=3, y=-7 et z=4

2

Tracer une figure

On considère le triangle \text{ABC} tel que \text{AB} = 5 cm, \text{AC} = 4 cm et \text{BC} = 7 cm.

1. Construire le triangle en vraie grandeur.

2. Construire le point \text{D} tel que \text{ABCD} soit un parallélogramme.

3. Construire le point \text{E} tel que \text{ABEC} soit un parallélogramme.

4. Par quelle transformation passe-t-on de \text{BCE} à \text{ADC} ?

3

Utiliser un repère orthonormé

On considère un repère orthonormé (\mathrm{O}\,; \mathrm{I}\,, \mathrm{J}). On prend pour unité le centimètre.

1. Tracer le repère puis placer les points \mathrm{A}(3\:;-2), \mathrm{B}(2\:;-3), \mathrm{C}(-3\:; 2) et \mathrm{D}(2\:; 3).

2. Construire le point \text{E} tel que \text{ACDE} soit un parallélogramme.

3. Construire le point \text{F} , image du point \text{B} par la translation transformant \text{C} en \text{D} .

4

Reconnaître des translations

Pour chaque image indiquer 4 paires de figures dont l'une est l'image de l'autre par translation.

1. Image 1 :

2. Image 2 :

5

Algo

Problème

Jeanne souhaite programmer avec Scratch le déplacement du robot \text{R} positionné au départ aux coordonnées (40\: ; 120) . Celui-ci se déplace comme de \text{A} vers \text{C} , puis passe par le point \text{D} tel \text{ABDC} soit un parallélogramme. Il rejoint ensuite l'origine du repère et se déplace par la translation transformant \text{B} en \text{A} .

1. Jeanne souhaite tracer le chemin avec GeoGebra. Construire la trajectoire du robot \text{R} .

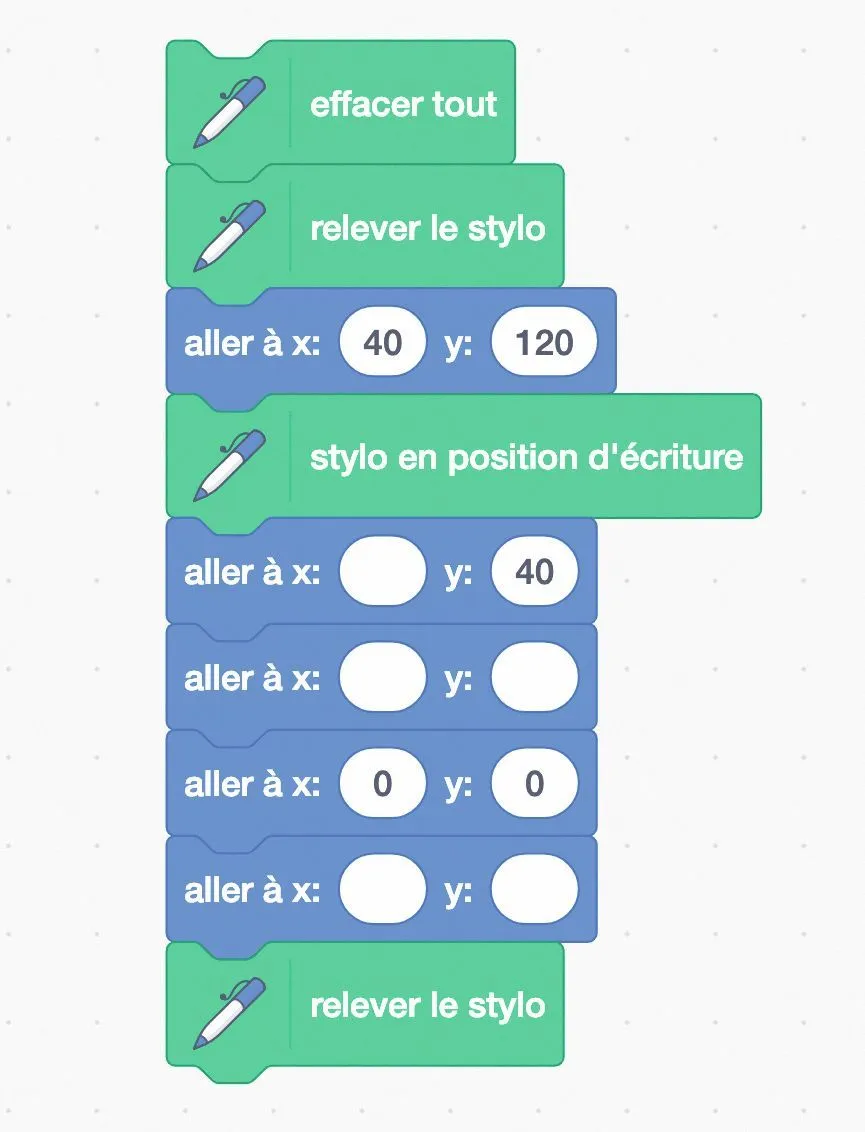
2. Compléter le programme de Jeanne.