Sommaire
Mes pages
N° Page
ouverture
p. 1-11
Fonctions
Géométrie
Statistiques et probabilités
Annexes
Nos dossiers d'actualité
Dossier d'actualité
/ 339
Page précédente
Chapitre 6
Activités

Notion de vecteur

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

A
Pratiquer le curling

Noter et représenter un vecteur, des vecteurs égaux et construire la somme de deux vecteurs.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Le curling, un des sports d'équipe les plus anciens du monde, voit le jour au XVIe siècle en Écosse où il est pratiqué en hiver sur les lacs et les étangs gelés. Le but est d'envoyer des pierres le plus près possible d'une cible circulaire dessinée sur la glace, appelée la « maison ». Maeva lance sa première pierre depuis le point \text{D} jusqu'au point \text{A} .

Pratiquer le curling

On représente la trajectoire de la pierre du point \text{D} à \text{A} à l'aide du vecteur \overrightarrow{\mathrm{DA}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Placeholder pour Photographie sportive : une joueuse de curling lance une pierre sur la glace. Uniforme rouge et noir.Photographie sportive : une joueuse de curling lance une pierre sur la glace. Uniforme rouge et noir.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
1
a) Maeva lance une deuxième pierre depuis le point \text{E} selon le déplacement donné par le vecteur \overrightarrow{\mathrm{DA}}. Sur l'image, indiquer \text{H}, la position d'arrivée de cette première pierre.


b) Elle lance ensuite une autre pierre toujours selon le déplacement donné par le vecteur \overrightarrow{\mathrm{DA}}. La trajectoire de la pierre se termine au point \text{F} . Sur l'image, indiquer \text{V}, la position de départ de cette pierre.

2
\text{H} est l'image de \text{E} par la translation de vecteur \overrightarrow{\mathrm{DA}} ou \overrightarrow{\mathrm{EH}} ou \overrightarrow{\mathrm{VF}}. Ces vecteurs sont égaux et on note par exemple \overrightarrow{\mathrm{DA}}=\overrightarrow{\mathrm{EH}}. Pourquoi les vecteurs \overrightarrow{\mathrm{TU}}, \overrightarrow{\mathrm{CG}} et \overrightarrow{\mathrm{RB}} ne sont-ils pas égaux à \overrightarrow{\mathrm{DA}} ?


3
En utilisant l'aide proposée, écrire des phrases décrivant les relations entre les points.
Aide
Deux vecteurs sont égaux lorsqu'ils ont le même sens, la même direction et la même norme (longueur).


4
On considère la figure ci‑dessous.

Pratiquer le curling

a) Maeva lance une pierre qui ricoche sur \text{R} puis termine en \text{M}. Construire le point \text{I} , image de \text{H} par la translation de vecteur \overrightarrow{\mathrm{DR}} puis le point \text{J}, image du point \text{I} par la translation de vecteur \overrightarrow{\mathrm{RM}}.

Remarque

On définit la somme de deux vecteurs par : \overrightarrow{\mathrm{DR}}+\overrightarrow{\mathrm{RM}}=\overrightarrow{\mathrm{DM}}. C'est la première fois que l'on additionne des objets qui ne soient pas des nombres !

b) Comment passe-t-on directement de \text{H} à \text{J} ?
Aide
« Si ... est un parallélogramme alors les vecteurs ... et ... sont égaux. » «  Si le point ... est l'image du point ... par la translation de vecteur ... alors ... est un parallélogramme. »
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Bilan
Quelles sont les trois caractéristiques d'un vecteur ? Comment représenter un vecteur et construire la somme de deux vecteurs ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

B
Formules et coordonnées de vecteurs

Dans un repère orthonormé, définir et utiliser les coordonnées d'un vecteur.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

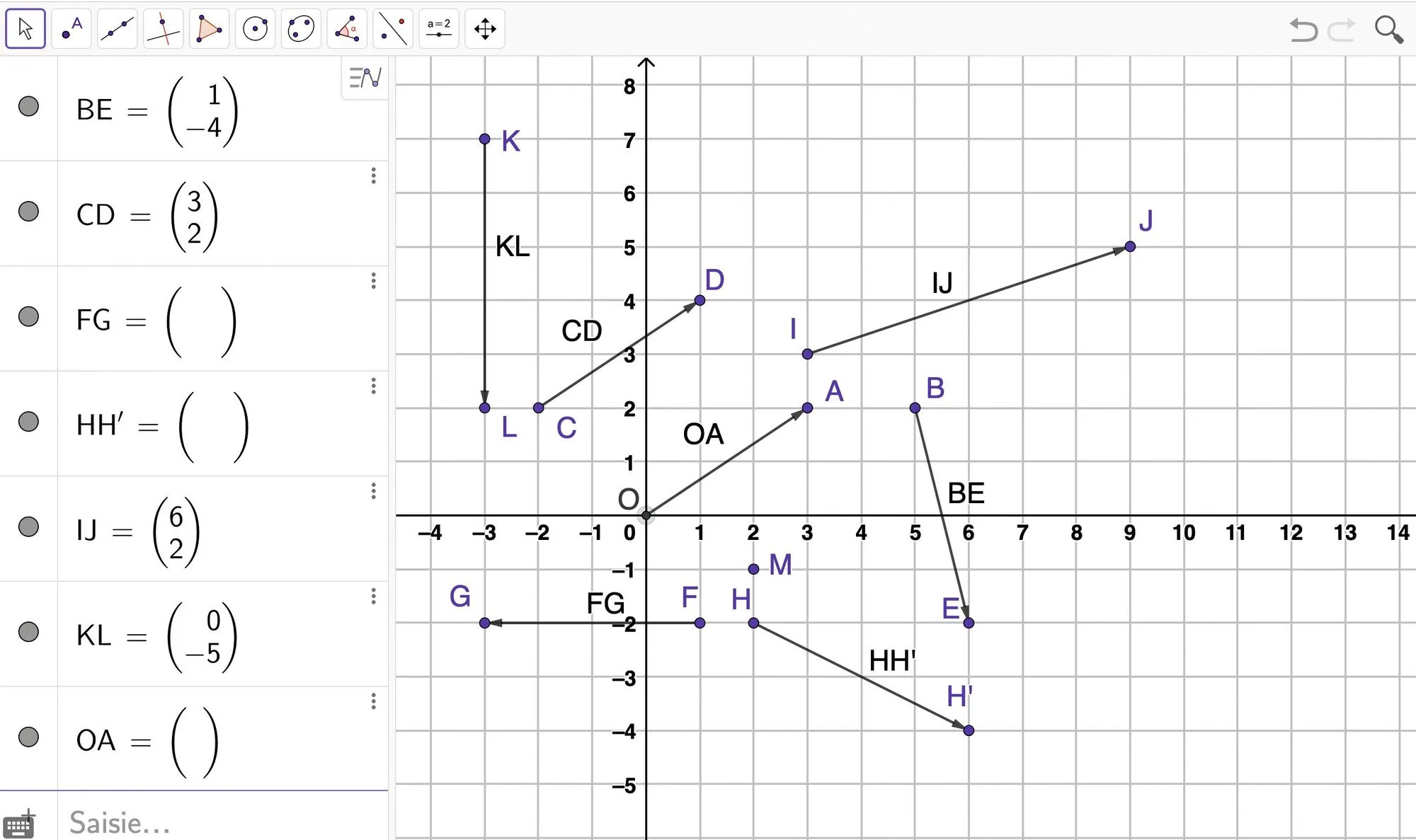
On a tracé des vecteurs dans un repère orthonormé à l'aide du logiciel GeoGebra. Les vecteurs \overrightarrow{\mathrm{OA}} et \overrightarrow{\mathrm{CD}} ont même sens, même direction et même norme (longueur). Le vecteur \overrightarrow{\mathrm{HH'}} est la somme des vecteurs \overrightarrow{\mathrm{OA}} et \overrightarrow{\mathrm{BE}}, c'est-à-dire \overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{BE}}=\overrightarrow{\mathrm{HH}^{\prime}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Placeholder pour Graphique montrant des vecteurs sur plan cartésien. Points (A, B, C...) reliés par flèches, coordonnées indiquées.Graphique montrant des vecteurs sur plan cartésien. Points (A, B, C...) reliés par flèches, coordonnées indiquées.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
1
Retrouver les coordonnées des vecteurs \overrightarrow{\mathrm{OA}}, \overrightarrow{\mathrm{FG}} et \overrightarrow{\mathrm{HH'}} en s'inspirant de celles de \overrightarrow{\mathrm{BE}} et \overrightarrow{\mathrm{CD}}.


2
Retrouver les coordonnées d'un vecteur à partir de celles de ses extrémités.


3
Retrouver les coordonnées des points \text{J} et \text{K} à partir de celles des vecteurs \overrightarrow{\mathrm{IJ}} et \overrightarrow{\mathrm{KL}}.


4
Retrouver les coordonnées du point \text{N} à partir de celles du vecteur \overrightarrow{\mathrm{MN}} \begin{pmatrix}{-8} \\ {0}\end{pmatrix}.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Bilan
Comment repérer un vecteur ? Comment calcule-t-on ses coordonnées ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

C
Somme de vecteurs dans un repère

Dans un repère orthonormé, calculer les coordonnées d'un vecteur somme.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Dans le repère orthonormé ci-contre, on a placé les points \text{A} , \text{B} , \text{C} , \text{D} et \text{E} et on a représenté les vecteurs \overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{AC}}, \overrightarrow{\mathrm{BC}}, \overrightarrow{\mathrm{CD}}, \overrightarrow{\mathrm{DE}} et \overrightarrow{\mathrm{CE}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Somme de vecteurs dans un repère
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
1
Par lecture graphique, donner les coordonnées des vecteurs \overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{BC}}, \overrightarrow{\mathrm{CD}}, et \overrightarrow{\mathrm{DE}}.


2
On admet que \overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}.
a) Justifier cette égalité à l'aide des translations.

b) Lire les coordonnées du vecteur \overrightarrow{\text{AC}} et faire le lien entre les coordonnées de \overrightarrow{\text{AC}} et celles de \overrightarrow{\text{AB}} et \overrightarrow{\text{BC}} ?


3
De même, calculer les coordonnées de \overrightarrow{\text{CE}}=\overrightarrow{\text{CD}}+\overrightarrow{\text{DE}}.


4
a) Quelles sont les coordonnées du vecteur nul \overrightarrow{0} ?

b) Après avoir calculé \overrightarrow{\mathrm{CD}}+\overrightarrow{\mathrm{DC}}, déterminer les coordonnées de \overrightarrow{\mathrm{DC}}. Cela est-il étonnant ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Bilan
Comment calculer les coordonnées d'un vecteur somme de deux vecteurs dans un repère ?

Page suivante

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille