Mathématiques 2de
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Nombres et calculs
Fonctions
Ch. 1
Généralités sur les fonctions
Ch. 2
Variations de fonctions
Ch. 3
Fonctions affines
Ch. 4
Fonctions de référence
Géométrie
Ch. 5
Repérage et configuration dans le plan
Ch. 6
Notion de vecteur
Ch. 7
Colinéarité de vecteurs
Ch. 8
Équations de droites
Statistiques et probabilités
Ch. 9
Informations chiffrées
Ch. 10
Statistiques descriptives
Ch. 11
Probabilités et échantillonnage
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de collège
Jeux de société
Chapitre 6
Entrainement 2
Vecteurs dans un repère
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
49
[Communiquer.]
On considère les vecteurs suivants dans un repère orthonormé (\mathrm{O}\,; \vec{i},\,\vec{j}).
2. Écrire les vecteurs dans la base (\vec{i},\vec{j}). comme l'exemple suivant : \overrightarrow{\mathrm{OB}}=3 \vec{i}+\overrightarrow{2 j}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
50
[Chercher.]À La Rochelle, un plaisancier navigue en notant sa position sur sa carte marine. \text{A} est son point de départ, \text{B} indique la position suivante, puis \text{C} , et ainsi de suite jusqu'au point \text{F}.
2. Lire les coordonnées des vecteurs \overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{BC}}, \overrightarrow{\mathrm{CD}}, \overrightarrow{\mathrm{DE}}, et \overrightarrow{\mathrm{EF}}.
3. Le lendemain, il réalise le trajet en sens inverse, de \text{F} vers \text{A} . Quelles sont les coordonnées des vecteurs successifs de son déplacement ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
51
[Représenter.]Une carte d'un trésor a été retrouvée avec le parchemin suivant : « Partant de \text{A} , 1 à l'ouest, 1 au sud ; 1 à l'ouest, 2 au sud ; 4 à l'est, 1 au nord ; 1 à l'ouest, 3 au sud ; 2 à l'ouest. » 1. Retrouver les différentes positions mentionnées dans le texte. On notera dans l'ordre les points de parcours de \text{B} jusqu'à \text{F} .
2. Donner les coordonnées des vecteurs associés : \overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{BC}}, \overrightarrow{\mathrm{CD}}, \overrightarrow{\mathrm{DE}} et \overrightarrow{\mathrm{EF}}.
3. En utilisant la même notation que celle du parchemin, quel déplacement permet de passer de \text{A} à \text{F} directement ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
52
Algo
[Calculer.]
On considère l'algorithme suivant. Les variables mentionnées sont des nombres réels.
\boxed{
\begin{array} { l }
\text{a} \leftarrow \text{x}_{\text{C}} - \text{x}_{\text{A}} \\
\text{b} \leftarrow \text{y}_{\text{C}} - \text{y}_{\text{A}} \\
\text{c} \leftarrow \text{x}_{\text{B}} - \text{x}_{\text{C}} \\
\text{d} \leftarrow \text{y}_{\text{B}} - \text{y}_{\text{C}} \\
\text{r} \leftarrow 0 \\
\text{Si } \text{a} = \text{c} \text{ et } \text{b} = \text{d} \text{ alors :} \\
\quad \text{r} \leftarrow 1 \\
\text{Fin Si }
\end{array}
}
1. On considère les points \text{A}(-1 \: ; 3), \text{B}(5 \: ; - 1) et
\text{C}(2 \: ; 1) .
a. Calculer les coordonnées de \overrightarrow{\text{AC}} et \overrightarrow{\text{CB}}.
b. Que peut-on dire des points \text{A}, \text{B} et \text{C} ?
2. Calculer les variables a , b , c et d à partir des points \text{A}, \text{B} et \text{C}.
3. En déduire le rôle de r .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
53
[Calculer.]
Dans chaque cas, \overrightarrow{u} et \overrightarrow{v} sont deux représentants d'un même vecteur. Calculer les valeurs de x et y.
1. \overrightarrow{u}\begin{pmatrix}{-3} \\ {5}\end{pmatrix} et \overrightarrow{v}\begin{pmatrix}{x-6} \\ {y+9}\end{pmatrix}
2. \overrightarrow{u}\begin{pmatrix}{11} \\ {-13}\end{pmatrix} et \overrightarrow{v}\begin{pmatrix}{2 x+5} \\ {3-2 y}\end{pmatrix}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
54
[Représenter.] On considère les points suivants dans un repère orthonormé (\mathrm{O}; \vec{i}, \vec{j}).
1. Déterminer graphiquement les coordonnées des objets suivants.
Le point \text{G} tel que \overrightarrow{\mathrm{AG}}\begin{pmatrix}{-4} \\ {4}\end{pmatrix}.
Le point \text{H} tel que \overrightarrow{\mathrm{HE}}\begin{pmatrix}{3} \\ {3}\end{pmatrix}.
Le point \text{M} tel que \overrightarrow{\mathrm{AM}}=4 \overrightarrow{i}+6\overrightarrow{j}.
Le point \text{N} tel que \overrightarrow{\mathrm{ND}}=\overrightarrow{\mathrm{AB}}.
Le point \text{P} tel que \overrightarrow{\mathrm{CP}}=\overrightarrow{\mathrm{DC}}.
2. Vérifier les réponses dans GeoGebra.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
55
GeoGebra
[Représenter.]
Lors d'une régate, trois voiliers s'élancent. Les
distances sont exprimées en milles marins (un mille
marin équivalent à 1 852 m). Le côté d'un carreau
mesure 2 milles marins.
1. Le voilier \mathrm{B}_{1} parcourt 14 milles vers l'est. Tracer le vecteur \overrightarrow{\mathrm{B}_{1} \mathrm{B}_{1}^{\prime}} correspondant à ce déplacement.
2. \mathrm{B}_{2} parcourt 8 milles en direction du nord-est puis 6
milles vers l'est. À l'aide d'un compas, tracer le vecteur
\overrightarrow{\mathrm{B}_{2} \mathrm{B}_{2}^{\prime}} correspondant à ce déplacement.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
56
[Calculer.] On considère quatre points \text{E} , \text{F} , \text{G} et \text{H} dans un repère orthonormé (\mathrm{O} ; \vec{i} , \vec{j}). Indiquer si \text{EFGH} est un parallélogramme dans les différents cas.
1. \mathrm{E}(2 \: ;-1), \mathrm{F}(8 \: ; -1), \mathrm{G}(10 \: ; 3) et \mathrm{H}(4 \: ; 3)
2. \mathrm{E}(1 \: ; -1), \mathrm{F}(0 \: ; 2), \mathrm{G}(8 \: ; -3) et \mathrm{H}(7 \: ; 0)
2. \mathrm{E}(1 \: ; -1), \mathrm{F}(0 \: ; 2), \mathrm{G}(8 \: ; -3) et \mathrm{H}(7 \: ; 0)
3. \mathrm{E}(-2\text{,}06 \: ; -1\text{,}78)\text{,} \mathrm{F}(0\text{,}92 \: ; -4{,}84)\text{,}\,\mathrm{G}(9\text{,}22 \: ; -2\text{,}08) et \mathrm{H}(6\text{,}1 \: ; 1\text{,}3)
4. \mathrm{E}(3 \: ; -4), \mathrm{F}(14 \: ; -4), \mathrm{G}(10 \: ; 4) et \mathrm{H}(-1 \: ; 4)
4. \mathrm{E}(3 \: ; -4), \mathrm{F}(14 \: ; -4), \mathrm{G}(10 \: ; 4) et \mathrm{H}(-1 \: ; 4)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
57
[Calculer.] On considère les points suivants dans un repère orthonormé (\mathrm{O}; \vec{i}, \vec{j}) : \mathrm{A}(-4\,;-3), \mathrm{B}(4\,;-2), \mathrm{C}(3\,; 2), \mathrm{D}(-5\, ; 1) et \mathrm{E}(2\, ; 6).
Répondre aux questions à l'aide des vecteurs en expliquant la démarche (on pourra éventuellement
1. Quelle est la nature du quadrilatère \text{ABCD} ?
2. Que représente le point \text{C} pour le segment [\text{BE}] ?
3. Le point \text{C} est-il l'image du point \text{E} par la translation de vecteur \overrightarrow{\text{DA}} ?
2. Que représente le point \text{C} pour le segment [\text{BE}] ?
3. Le point \text{C} est-il l'image du point \text{E} par la translation de vecteur \overrightarrow{\text{DA}} ?
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
58
[Raisonner.]
On considère les points suivants dans un repère orthonormé (\mathrm{O}; \vec{i}, \vec{j}) : \text{A}(3\: ; 5) , \text{C}(7\: ; - 9) et \text{M}(-5\: ; 5). \text{P} est le point de coordonnées (5\: ; - 2). 1. Calculer les coordonnées du point \text{M}', symétrique de \text{M} par la symétrie de centre \text{P .}
2. Vérifier que le point \text{C} est l'image de \text{P} par la translation du vecteur \overrightarrow{\text{AP}}. Que peut-on en déduire sur \text{P} ?
3. Démontrer que \text{AMCM}' est un parallélogramme.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
59
[Calculer.] On considère les points et les vecteurs suivants dans un repère (\text{O} ; \vec{i} , \vec{j}).
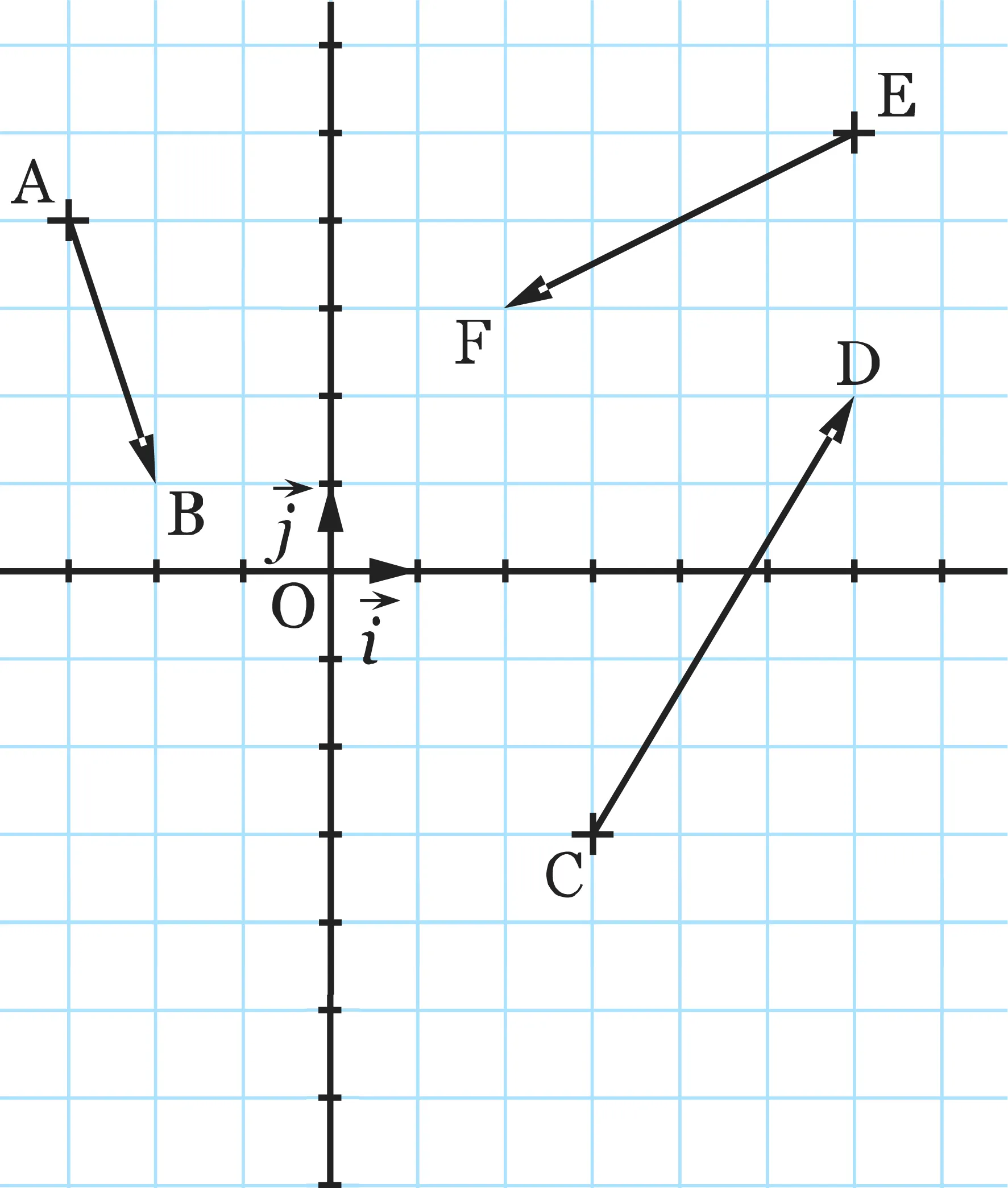
2. Calculer les coordonnées de \overrightarrow{v}
telles que \overrightarrow{v}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{EF}}. Construire le point \text{J} tel que \overrightarrow{\mathrm{OJ}}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{EF}}.
3. Calculer les coordonnées de \overrightarrow{w} telles que \overrightarrow{w}=\overrightarrow{\mathrm{CD}}+\overrightarrow{\mathrm{EF}}. Construire le point \text{H} tel que \overrightarrow{\mathrm{OH}}=\overrightarrow{\mathrm{CD}}+\overrightarrow{\mathrm{EF}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
60
[Calculer.]
Dans un repère orthonormé (\text{O} ; \vec{i} , \vec{j}), on considère les points \text{A}(-8 \: ; 3), \text{B}(4 \: ; 2) et \text{C}(11 \: ; -3). 1. Calculer les coordonnées des vecteurs \overrightarrow{u}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}, \overrightarrow{v}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}} et \overrightarrow{w}=\overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{BC}}.
2. Écrire chaque vecteur \overrightarrow{u}, \overrightarrow{v} et \overrightarrow{w} uniquement en fonction de \overrightarrow{i} et \overrightarrow{j}.
3. Calculer les coordonnées du vecteur \overrightarrow{z}=\overrightarrow{u}+\overrightarrow{v}+\overrightarrow{w}. Que constate-t-on ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
61
[Raisonner.]
Dans un repère (\text{O} ; \vec{i} , \vec{j}), on considère les points \text{A}( 5 \: ; -6), \text{B} (4 \: ; 2) et \text{D}(4 \: ; -7).
Quelles sont les coordonnées du point \text{C}(x \: ; y) sachant que le vecteur \overrightarrow{u}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{CD}} a pour coordonnées \overrightarrow{u}\begin{pmatrix}{5} \\ {4}\end{pmatrix} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
62
[Calculer.]
Dans un repère orthonormé (\text{O} ; \vec{i} , \vec{j}), on considère les points \text{R}(5 \: ; 1), \text{S}(2 \: ; -4), \text{T}(-3 \: ; 1), \text{U}(1 \: ; 4) et \text{V}(3 \: ; 5).
Calculer les coordonnées du point \text{W}(x \: ; y) telles que \overrightarrow{\mathrm{VW}}=\overrightarrow{\mathrm{RS}}+\overrightarrow{\mathrm{TU}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
63
[Représenter.] Lors d'une course en mer, un voilier se déplace sous l'action combinée du vent et du courant marin associés aux vecteurs \overrightarrow{v} et \overrightarrow{c}. Le vecteur déplacement est la somme de \overrightarrow{v} et \overrightarrow{c}. Le départ est l'origine du repère.
Soit \text{M} (x \: ; y ) le point tel que \overrightarrow{\text{OM}} = \overrightarrow{v} + \overrightarrow{c}. Le skipper souhaite connaître les coordonnées de \text{M}. 1. Le repère ci-dessus est l'écran du GPS du voilier. Quelle difficulté rencontre-t-il pour localiser \text{M} ?
2. Comment aider le skipper à calculer les coordonnées du point \text{M} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
64
En Physique
[Calculer.]On considère un objet soumis à trois forces. On a représenté cet objet dans GeoGebra par le point \text{A} et ces trois forces par les vecteurs \overrightarrow{u}, \overrightarrow{v} et \overrightarrow{w}.
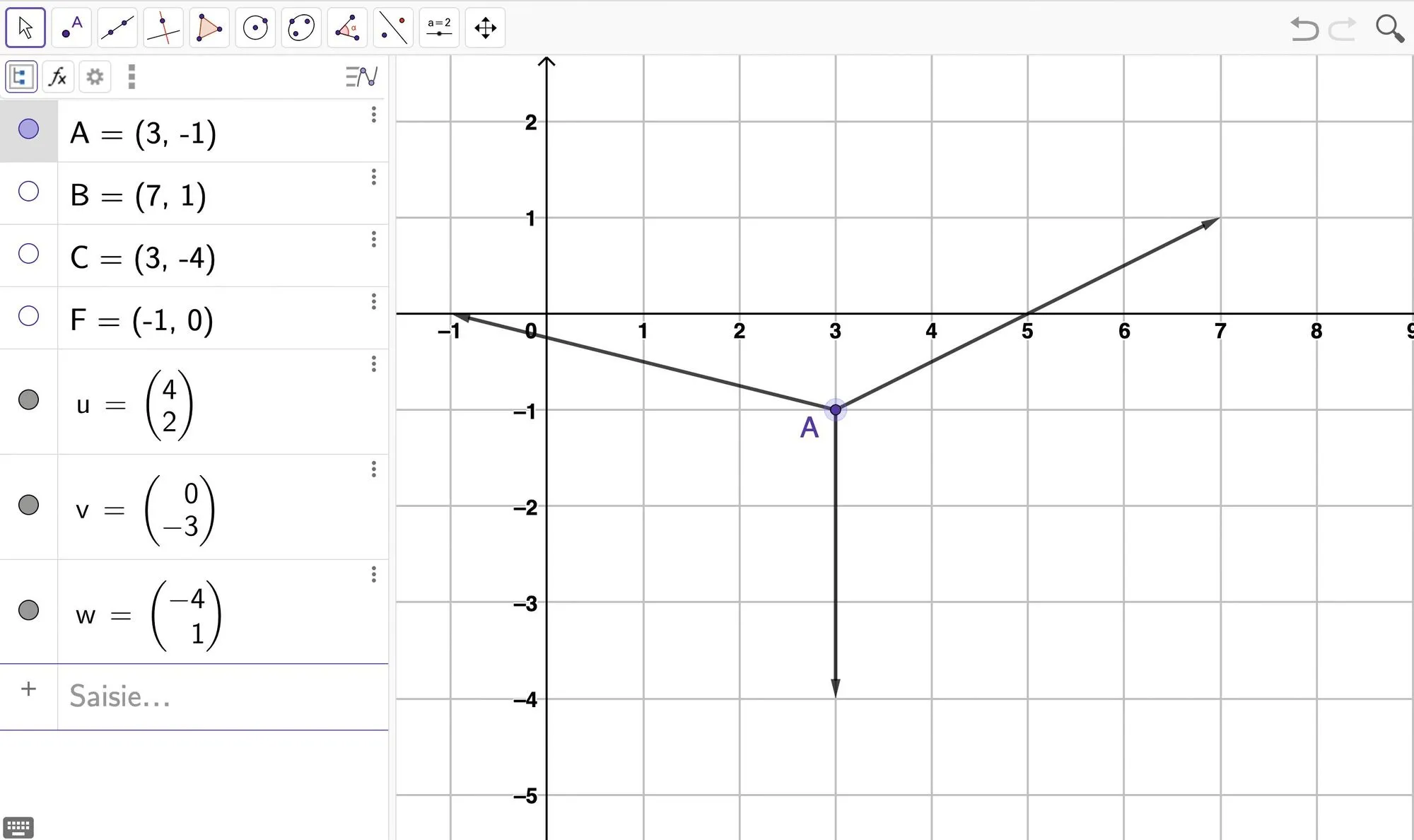
2. On dit que les forces se compensent lorsque \overrightarrow{u} + \overrightarrow{v} + \overrightarrow{w} = \overrightarrow{0}. Est-ce le cas ici ? Justifier.
3. Calculer l'intensité de chacune d'entre elles.
Aide
L'intensité d'une force est la norme du vecteur la représentant.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
65
[Représenter.]On se place dans un repère (\text{O} ; \vec{i} , \vec{j}). La figure ci-dessous représente deux voitures \text{A} et \text{B} qui roulent selon les vecteurs vitesses \overrightarrow{\text{V}_{\text{A}}} = 90 \overrightarrow{i} et \overrightarrow{\text{V}_{\text{B}}} = 60 \overrightarrow{i}.
La norme de chaque vecteur est la vitesse de chaque voiture en km/h.
1. Déterminer les coordonnées de chaque vecteur puis
en déduire alors la vitesse de chaque voiture.
2. Un enfant assis sur la banquette arrière de la voiture \text{B} voit la voiture \text{A} le dépasser à une vitesse relative de \text{A} par rapport à \text{B} égale à \left\|\overrightarrow{\mathrm{V}_{\mathrm{A}}}-\overrightarrow{\mathrm{V}_{\mathrm{B}}}\right\|.
Calculer cette vitesse ? Est-ce étonnant ?
3. Quelle est la vitesse relative de la voiture \text{A} par rapport à \text{B} lorsque \overrightarrow{\text{V}_{\text{A}}} = 90 \overrightarrow{i} et \overrightarrow{\text{V}_{\text{B}}} = -60 \overrightarrow{i} ? Détailler la situation dans ce cas.
2. Un enfant assis sur la banquette arrière de la voiture \text{B} voit la voiture \text{A} le dépasser à une vitesse relative de \text{A} par rapport à \text{B} égale à \left\|\overrightarrow{\mathrm{V}_{\mathrm{A}}}-\overrightarrow{\mathrm{V}_{\mathrm{B}}}\right\|.
Calculer cette vitesse ? Est-ce étonnant ?
3. Quelle est la vitesse relative de la voiture \text{A} par rapport à \text{B} lorsque \overrightarrow{\text{V}_{\text{A}}} = 90 \overrightarrow{i} et \overrightarrow{\text{V}_{\text{B}}} = -60 \overrightarrow{i} ? Détailler la situation dans ce cas.
Dans la vie professionnelle
L'ingénieur(e) en mécanique des fluides peut se spécialiser dans l'amélioration des différents moyens de transports pour lesquels les paramètres s'apparentent à la mécanique des fluides (par exemple, les embouteillages). Pour cela, de nombreuses composantes sont étudiées et les vecteurs (au sens large du terme) sont nécessaires à la résolution de certains problèmes.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
