Théorème de Ménélaüs

1. En utilisant \overrightarrow{\mathrm{BA}'}=\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{CA}'}, montrer que \overrightarrow{\mathrm{BA}'}=\dfrac{a}{a-1} \overrightarrow{\mathrm{BC}}.

2. Exprimer les coordonnées de \text{A}' en fonction de a, celles de \text{B}' en fonction b et celles de \text{C}' en fonction de c.

1. Construire les points \text{A}, \text{B} et \text{C}.
2. Créer trois curseurs nommés a , b et c , (incrémentation de 0{,}01, min = -10 , max = 10 ) avec la commande
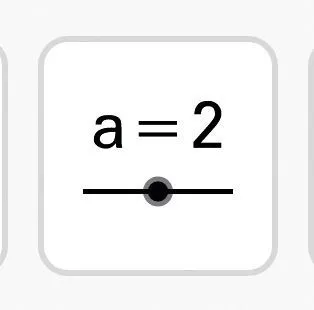3. À l'aide des questions préliminaires, placer les points \text{A}', \text{B}' et \text{C}' puis tracer la droite (\text{A}'\text{B}'). Par exemple, pour le point \text{A}', on peut écrire :

4. Dans chacun des cas suivants, conjecturer une valeur de c pour que les points \text{A}', \text{B}' et \text{C}' soient alignés.

a = -0{,}5 et b = 0{,}4

a = 0{,}2 et b = -5

a = 4 et b = -0{,}5

5. Faire d'autres tests et conjecturer une relation entre les coefficients a , b et c pour que les points \text{A}', \text{B}' et \text{C}' soient alignés.
Indication : tester différentes opérations entre les 3 coefficients (ex : a + b + c ).

Le tableur va nous permettre de tester différentes valeurs de a et b en fixant la valeur de c, et d'essayer d'en extraire une conjecture. Dans cette méthode, nous allons fixer la valeur c = 0{,}5 . 1. Calculer les coordonnées de \text{C}'.

2. Exprimer les coordonnées de \overrightarrow{\mathrm{A}^{\prime} \mathrm{B}^{\prime}} et \overrightarrow{\mathrm{A}^{\prime} \mathrm{C}^{\prime}} en fonction de a et b .

3. Dans un tableur, reproduire le tableau ci-dessous (la première colonne étant les valeurs de a et la première ligne, les valeurs de b).

4. Dans la case B2, écrire une formule qui permet de calculer le déterminant de \overrightarrow{\mathrm{A}^{\prime} \mathrm{B}^{\prime}} et \overrightarrow{\mathrm{A}^{\prime} \mathrm{C}^{\prime}} quand a = -2 et b = -2 puis étirer cette cellule pour calculer le déterminant pour toutes les cellules à l'écran en s'aidant des cellules A2 et B1 et en n'oubliant pas d'utiliser le symbole \bf{\$}.

5. Pour quelles valeurs de a et b les vecteurs \overrightarrow{\mathrm{A}^{\prime} \mathrm{B}^{\prime}} et \overrightarrow{\mathrm{A}^{\prime} \mathrm{C}^{\prime}} sont-ils colinéaires (sans oublier que c = 0{,}5 ) ?

6. Conjecturer une relation entre les coefficients a , b et c pour que les points \text{A} , \text{B} et \text{C} soient alignés.
Indication : tester différentes opérations entre les 3 coefficients (ex : a + b + c ).