Mathématiques Expertes Terminale
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Nombres complexes
Ch. 1
Nombres complexes, point de vue algébrique
Ch. 2
Nombres complexes, point de vue géométrique
Arithmétique
Ch. 3
Divisibilité dans Z
Ch. 4
PGCD et applications
Ch. 5
Nombres premiers
Graphes et matrices
Ch. 6
Calcul matriciel et applications aux graphes
Ch. 7
Suites et matrices
Annexes
Cahier d'algorithmique et de programmation
Partie 3
Histoire des mathématiques
Graphes et matrices
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Histoire Les graphes, d'une devinette à une nouvelle théorie
De passage à Königsberg (aujourd'hui Kaliningrad en Russie), Leonhard Euler (1707‑1783) est confronté à un problème posé par ses habitants : est‑il possible de passer par tous les ponts de la ville une, et une seule, fois ? (Voir le plan de la ville ci‑contre.)

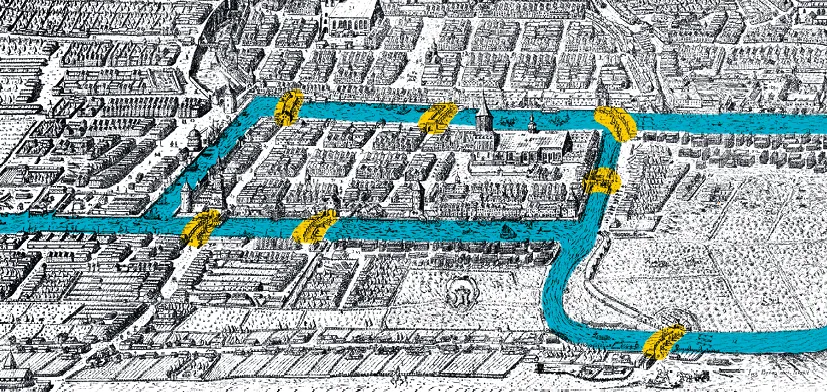
Plan de la ville de Königsberg en 1613.
Euler raisonne alors sur un schéma de type nouveau (ci‑contre) qui est une figure géométrique dont la forme et la longueur des arêtes n'ont pas d'importance, ni l'angle qu'elles forment les unes avec les autres. Sa démonstration ne se base donc pas sur tous les résultats connus de la géométrie de l'époque et donne naissance à deux nouveaux domaines mathématiques : la topologie et la théorie des graphes.

Représentation schématique de Königsberg selon la méthode d'Euler.
Pour résoudre des problèmes liés à l'électricité, le physicien Gustav Kirchhoff (1824‑1887) est le premier, en 1847, à utiliser les graphes. Il créa les arbres (graphe sans boucle) qu'Arthur Cayley (1821‑1895) développa par la suite.
Depuis, l'utilisation des graphes s'est généralisée dans bien des domaines comme les jeux, les probabilités (chaînes de Markov), l'économie, la sociologie (sociogramme ci‑contre), l'intelligence artificielle, etc.
Depuis, l'utilisation des graphes s'est généralisée dans bien des domaines comme les jeux, les probabilités (chaînes de Markov), l'économie, la sociologie (sociogramme ci‑contre), l'intelligence artificielle, etc.

Exemple de sociogramme
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Histoire Les matrices : résoudre des systèmes d'équation et des problèmes géométriques
Le 8e des neuf chapitres sur l'Art des mathématiques (livre récapitulant les savoirs mathématiques de la Chine Antique, IIe siècle av. J.‑C., Ier siècle ap. J.‑C.) porte sur la résolution de systèmes d'équations à deux ou trois inconnues en n'utilisant que les coefficients de ces équations. La méthode proposée peut être considérée comme l'ancêtre d'une méthode matricielle.
Girolamo Cardano (1501‑1576) propose dans son Ars Magna (1545) la « regula de modo », un calcul qui permet de savoir si un système de deux équations à deux inconnues admet un unique couple solution. Ce résultat ouvrira sur le déterminant de matrices.
Indépendamment l'un de l'autre, Seki Kowa (1642‑1708) et Gottfried Wilhelm Leibniz (1646‑1716) développent cette notion pour les systèmes 3 \times 3 et 4 \times 4.
Des mathématiciens comme Cramer (1704‑1752), Vandermonde (1735‑1796), Laplace (1749‑1827), Lagrange (1736‑1813), Gauss (1777‑1855) ou encore Cauchy (1789‑1857) travaillent sur les déterminants, en étudiant leurs propriétés et en développant les premières théories sur le sujet.
Girolamo Cardano (1501‑1576) propose dans son Ars Magna (1545) la « regula de modo », un calcul qui permet de savoir si un système de deux équations à deux inconnues admet un unique couple solution. Ce résultat ouvrira sur le déterminant de matrices.
Indépendamment l'un de l'autre, Seki Kowa (1642‑1708) et Gottfried Wilhelm Leibniz (1646‑1716) développent cette notion pour les systèmes 3 \times 3 et 4 \times 4.
Des mathématiciens comme Cramer (1704‑1752), Vandermonde (1735‑1796), Laplace (1749‑1827), Lagrange (1736‑1813), Gauss (1777‑1855) ou encore Cauchy (1789‑1857) travaillent sur les déterminants, en étudiant leurs propriétés et en développant les premières théories sur le sujet.


James Sylvester


Arthur Cayley
James Sylvester (1814‑1897), influencé par son ami Arthur Cayley (1821‑1895), utilise les matrices et les déterminants afin de donner des solutions simplifiées à un problème géométrique. Les deux hommes deviennent amis et leurs échanges contribuent à l'élaboration d'une théorie algébrique sur les matrices. En 1858, Cayley publie son Memoir on the Theory of Matrices. Les travaux d'Eduard Weyr (1852‑1903) permettent ensuite de lier les matrices aux fonctions vectorielles. Le début du XXe siècle donnera alors une place centrale aux matrices et aux déterminants dans l'étude de la géométrie.

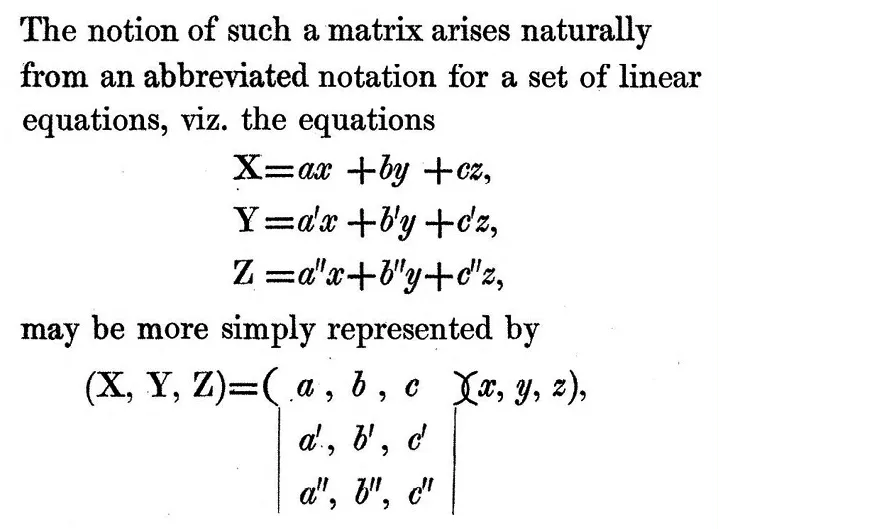
Extrait de Memoir on the Theory of Matrices de Cayley
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
