Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Nombres complexes
Ch. 1
Nombres complexes, point de vue algébrique
Ch. 2
Nombres complexes, point de vue géométrique
Arithmétique
Ch. 3
Divisibilité dans Z
Ch. 4
PGCD et applications
Ch. 5
Nombres premiers
Graphes et matrices
Ch. 6
Calcul matriciel et applications aux graphes
Ch. 7
Suites et matrices
Annexes
Cahier d'algorithmique et de programmation
Chapitre 6
Entraînement 2
Les graphes
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
67
Flash
Construire un graphe d'ordre 5 possédant un sommet de degré 1, un sommet de degré 3 et tel que tous ses autres sommets soient de degré pair.
Cette fonctionnalité est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
68
Flash
Ajouter autant d'arêtes que nécessaire pour que le graphe ci‑dessous soit complet.
Cette fonctionnalité est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
69
Flash
Quelle est la longueur de la plus petite chaîne passant par tous les sommets du graphe ci‑dessous et revenant au sommet de départ ?
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
70
[Raisonner.]
Soit n un entier naturel non nul.
Justifier que si un graphe simple d'ordre n (c'est-à-dire un graphe ayant au plus une arête entre deux sommets et sans boucle) est complet, alors chaque sommet est de degré n - 1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
71
[Modéliser.]
Pour se rendre de Paris à New York en avion, un voyageur
a plusieurs choix de vols parmi lesquels on trouve :
→ des vols directs
→ des vols avec une escale
→ des vols avec deux escales
→ des vols directs
- Paris - New York
→ des vols avec une escale
- Paris - Londres - New York
- Paris - Zurich - New York
- Paris - Lisbonne - New York
- Paris - Boston - New York
→ des vols avec deux escales
- Paris - Zurich - Toronto - New York
- Paris - Zurich - Montréal - New York
- Paris - Montréal - Ottawa - New York
- Paris - Madrid - Londres - New York
Représenter ces différents vols sur un graphe orienté,
dont les sommets seront les villes par lesquelles
transite le voyageur.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
72
[Modéliser.]
À la fin de la seconde, un élève orienté en première
générale a le choix de suivre ou non l'enseignement de
spécialité mathématiques.
Un élève n'ayant pas suivi l'enseignement de spécialité en première peut suivre l'enseignement facultatif mathématiques complémentaires en terminale.
Un élève ayant suivi l'enseignement de spécialité en première peut l'abandonner et ne plus faire de mathématiques, l'abandonner et suivre l'enseignement facultatif mathématiques complémentaires ou le poursuivre en terminale.
S'il poursuit l'enseignement de spécialité en terminale, il peut choisir de suivre l'enseignement facultatif mathématiques expertes.
Représenter les différents parcours en mathématiques possibles d'un lycéen par un graphe, dont les sommets seront les différents enseignements possibles.
Un élève n'ayant pas suivi l'enseignement de spécialité en première peut suivre l'enseignement facultatif mathématiques complémentaires en terminale.
Un élève ayant suivi l'enseignement de spécialité en première peut l'abandonner et ne plus faire de mathématiques, l'abandonner et suivre l'enseignement facultatif mathématiques complémentaires ou le poursuivre en terminale.
S'il poursuit l'enseignement de spécialité en terminale, il peut choisir de suivre l'enseignement facultatif mathématiques expertes.
Représenter les différents parcours en mathématiques possibles d'un lycéen par un graphe, dont les sommets seront les différents enseignements possibles.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
73
[Raisonner.]
1. Montrer que la somme des degrés des sommets d'un graphe est égale au double du nombre d'arêtes.
2. a. Un octogone et toutes ses diagonales forment un graphe. Quel est le nombre d'arêtes de ce graphe ?
b. Qu'en est‑il si l'on considère un polygone qui a 1 000 côtés ?
3. Un club d'échecs souhaite organiser un tournoi pour quinze joueurs. Lors des phases de sélection, on souhaite que chaque joueur en affronte cinq autres.
Est‑ce possible ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
74
[Modéliser.]
Le graphe ci‑dessous représente les autoroutes entre les principales villes de la région Hauts‑de‑France :
Abbeville \text{(A)}, Boulogne‑sur‑Mer \text{(B)}, Calais \text{(C)}, Dunkerque \text{(D)}, Lens \text{(E)}, Beauvais \text{(I)}, Lille \text{(L)}, Amiens \text{(M)}, Laon \text{(N)}, Saint‑Omer \text{(O)}, Péronne \text{(P)}, Saint‑Quentin \text{(Q)}, Senlis \text{(S)} et Valenciennes \text{(V)}.
Le zoom est accessible dans la version Premium.
1. Quel est l'ordre de ce graphe ?
2. a. Quels sont les sommets de plus haut degré ?
b. Quels sont les sommets de plus petit degré ?
3. Les sommets \text{L} et \text{E} sont‑ils adjacents ?
4. Ce graphe est‑il complet ? Justifier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
75
[Représenter.]
L'illustration ci‑après représente la ville de
Königsberg au XVIIIe siècle et ses sept ponts.
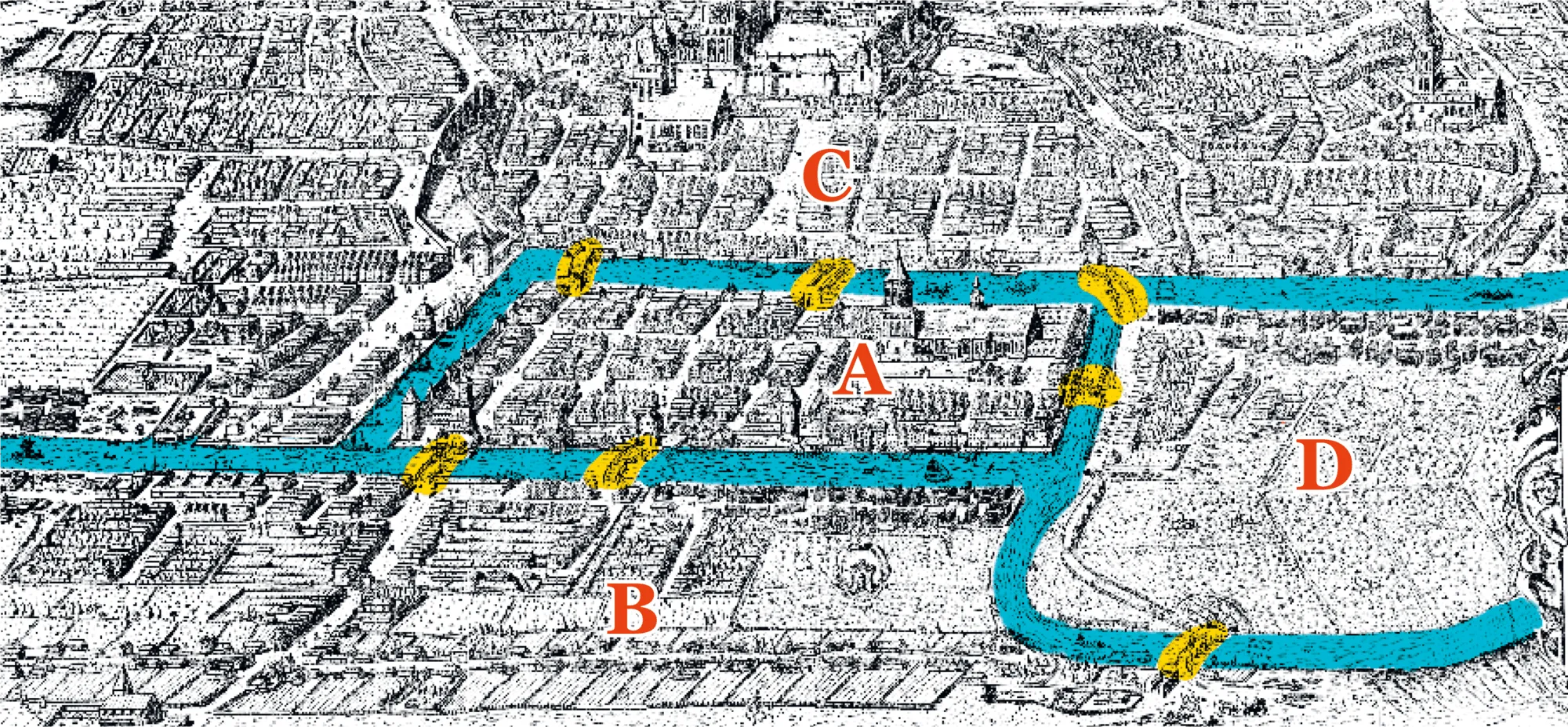En se trouvant dans l'un des quartiers \text{A}, \text{B}, \text{C} ou \text{D}, on peut accéder à un autre quartier en empruntant l'un des ponts.
Le zoom est accessible dans la version Premium.
Histoire des maths
C'est Euler qui, en 1759, rapporte cette configuration
et le problème suivant : « Peut‑on arranger son
parcours de telle sorte que l'on passe sur chaque pont,
et que l'on ne puisse y passer qu'une seule fois ? ». Il
étudie le problème en toute généralité et montre qu'il
n'a, dans ce cas, pas de solution.
1. Représenter la situation par un graphe.
2. Ce graphe est‑il complet ? Justifier.
3. Ce graphe est‑il connexe ? Justifier.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
76
[Chercher.]
D'après bac ES, Centres étrangers, juin 2019
Un restaurateur se fournit auprès de cinq producteurs locaux.
Le graphe ci‑dessous représente la situation géographique du restaurateur et de ses fournisseurs, les arêtes correspondant au réseau routier et les sommets aux producteurs : éleveur \text{(E)}, fromager \text{(F)}, maraîcher \text{(M)}, pisciculteur \text{(P)}, restaurateur \text{(R)} et vigneron \text{(V)}.
Le zoom est accessible dans la version Premium.
1. Quel est l'ordre de ce graphe ?
2. a. Quel est le degré du sommet \text{P} ?
b. Citer un sommet de degré inférieur ou égal à 3.
c. Citer deux sommets de degré impair.
3. Citer deux sommets adjacents et deux sommets qui ne sont pas adjacents.
4. Ce graphe est-il complet ? Justifier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
77
[Modéliser.]
Le plan d'un parc zoologique est donné ci-dessous.
Le zoom est accessible dans la version Premium.
1. Modéliser le plan du parc zoologique par un graphe.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
2. Quel est l'ordre de ce graphe ?
3. Quel est le sommet de plus petit degré ?
4. Ce graphe est‑il complet ? Justifier.
5. Ce graphe est‑il connexe ? Justifier.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah