Mathématiques Expertes Terminale
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Nombres complexes
Ch. 1
Nombres complexes, point de vue algébrique
Ch. 2
Nombres complexes, point de vue géométrique
Arithmétique
Ch. 3
Divisibilité dans Z
Ch. 4
PGCD et applications
Ch. 5
Nombres premiers
Graphes et matrices
Ch. 6
Calcul matriciel et applications aux graphes
Ch. 7
Suites et matrices
Annexes
Cahier d'algorithmique et de programmation
Chapitre 6
TP / TICE 1
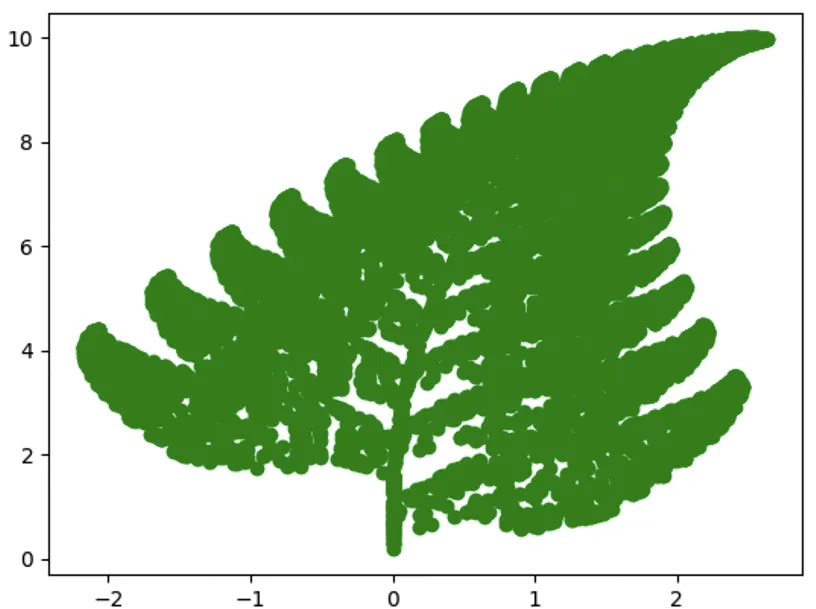
La fougère de Barnsley
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Les matrices peuvent être utilisées pour représenter des transformations du plan (rotation, symétrie, etc.). Nous allons utiliser cette représentation matricielle des transformations du plan pour tracer une suite aléatoire de points \left(\mathrm{A}_{n}\right)_{n \in \mathbb{N}} de la façon suivante :
La suite de points ainsi obtenue forme une fractale appelée fougère de Barnsley.
Questions préliminaires :
1. Quelles sont les coordonnées possibles du point \mathrm{A}_{1} ?
2. Soit n \in \mathbb{N} tel que \mathrm{A}_{n} admette pour coordonnées (0{,}5\,; 1). Calculer les coordonnées possibles de \mathrm{A}_{n+1}.
- Le premier point de cette suite est \mathrm{A}_{0}(0\,; 0) ;
- Pour tout n \in \mathbb{N}, on note \left(x_{n}\,; y_{n}\right) les coordonnées de \mathrm{A}_{n} et on a :
- \left(\begin{array}{l} x_{n+1} \\ y_{n+1} \end{array}\right)=\left(\begin{array}{cc} 0 & 0 \\ 0 & 0{,}16 \end{array}\right)\left(\begin{array}{l} x_{n} \\ y_{n} \end{array}\right)+\left(\begin{array}{l} 0 \\ 0 \end{array}\right) avec une probabilité de 0{,}01 ;
- \left(\begin{array}{l} x_{n+1} \\ y_{n+1} \end{array}\right)=\left(\begin{array}{cc} 0{,}85 & 0{,}04 \\ -0{,}04 & 0{,}85 \end{array}\right)\left(\begin{array}{c} x_{n} \\ y_{n} \end{array}\right)+\left(\begin{array}{c} 0 \\ 1{,}6 \end{array}\right) avec une probabilité de 0{,}85 ;
- \left(\begin{array}{l} x_{n+1} \\ y_{n+1} \end{array}\right)=\left(\begin{array}{cc} 0{,}2 & -0{,}26 \\ 0{,}23 & 0{,}22 \end{array}\right)\left(\begin{array}{l} x_{n} \\ y_{n} \end{array}\right)+\left(\begin{array}{c} 0 \\ 1{,}6 \end{array}\right) avec une probabilité de 0{,}07 ;
- \left(\begin{array}{l} x_{n+1} \\ y_{n+1} \end{array}\right)=\left(\begin{array}{cc} -0{,}15 & 0{,}28 \\ 0{,}26 & 0{,}24 \end{array}\right)\left(\begin{array}{c} x_{n} \\ y_{n} \end{array}\right)+\left(\begin{array}{c} 0 \\ 0{,}44 \end{array}\right) avec une probabilité de 0{,}07.
La suite de points ainsi obtenue forme une fractale appelée fougère de Barnsley.
Questions préliminaires :
1. Quelles sont les coordonnées possibles du point \mathrm{A}_{1} ?
2. Soit n \in \mathbb{N} tel que \mathrm{A}_{n} admette pour coordonnées (0{,}5\,; 1). Calculer les coordonnées possibles de \mathrm{A}_{n+1}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Tracer la fougère de Barnsley en utilisant une des deux méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1Python
import matplotlib.pyplot as plt from random import * def transformation1(A): A = (0,0.16*A[1]) return(A) def transformation2(A): A = (0.85*A[0] + 0.04*A[1],-0.04*A[0] + 0.85*A[1]+1.6) return(A) def transformation3(A): A = (0.2*A[0] - 0.26*A[1],0.23*A[0] + 0.22*A[1]+1.6) return(A) def transformation4(A): A = (...,...) return(A) def fougere(n): A = (0,0) x = [] y = [] for i in range(n): r = random() if r < ... : A = transformation1(A) elif r < ... : A = transformation2(A) elif r < ... : A = transformation3(A) else : A = transformation4(A) x.append(A[0]) y.append(A[1]) plt.plot(x,y,'o') plt.show()
1. a. Expliquer les lignes 4 et 18 du programme : quel rôle jouent-elles ?
b. Compléter la ligne 17 du programme.
2. Compléter les lignes 26, 28 et 30 du programme Python.
3. Utiliser le programme Python pour tracer la fougère de Barnsley pour 400, 10 000, puis 100 000 points.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2GeoGebra
Télécharger le fichier GeoGebra de cette
construction .
1. Ouvrir la fenêtre tableur de ce fichier GeoGebra, puis entrer en D4 une formule permettant d'obtenir un nombre aléatoire compris entre 0 et 1.
2. Expliquer les formules \color{purple}=\mathbf{A} \mathbf{4}(\mathbf{1}, \mathbf{1}) et \color{purple}=\mathbf{A}\mathbf{4}(\mathbf{2}, \mathbf{1}) entrées en B4 et C4 : que permettent‑elles de faire ? À quoi correspondent \color{purple}(\mathbf{1}, \mathbf{1}) et \color{purple}(\mathbf{2}, \mathbf{1}) dans ces formules ?
3. Compléter la formule inscrite en A5 de manière à ce qu'elle contienne les coordonnées du point \mathrm{A}_{1}.
4. Copier vers le bas les formules entrées en A5, B4, C4 et D4 de manière à faire apparaître dans la colonne B les abscisses et dans la colonne C les ordonnées des 400 premiers points \mathrm{A}_{n} de la suite.
5. Sélectionner la plage contenant ces deux coordonnées, faire un clic droit, puis sélectionner \color{purple}\mathbf{Créer} et enfin l'outil \color{purple}\mathbf{Liste\,de\,points}, pour afficher la fougère de Barnsley dans la fenêtre graphique.
1. Ouvrir la fenêtre tableur de ce fichier GeoGebra, puis entrer en D4 une formule permettant d'obtenir un nombre aléatoire compris entre 0 et 1.
2. Expliquer les formules \color{purple}=\mathbf{A} \mathbf{4}(\mathbf{1}, \mathbf{1}) et \color{purple}=\mathbf{A}\mathbf{4}(\mathbf{2}, \mathbf{1}) entrées en B4 et C4 : que permettent‑elles de faire ? À quoi correspondent \color{purple}(\mathbf{1}, \mathbf{1}) et \color{purple}(\mathbf{2}, \mathbf{1}) dans ces formules ?
3. Compléter la formule inscrite en A5 de manière à ce qu'elle contienne les coordonnées du point \mathrm{A}_{1}.
4. Copier vers le bas les formules entrées en A5, B4, C4 et D4 de manière à faire apparaître dans la colonne B les abscisses et dans la colonne C les ordonnées des 400 premiers points \mathrm{A}_{n} de la suite.
5. Sélectionner la plage contenant ces deux coordonnées, faire un clic droit, puis sélectionner \color{purple}\mathbf{Créer} et enfin l'outil \color{purple}\mathbf{Liste\,de\,points}, pour afficher la fougère de Barnsley dans la fenêtre graphique.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
