Enseignement scientifique Terminale - 2024

Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Sciences, climat et société
Ch. 1
L’atmosphère terrestre et la vie
Ch. 2
La complexité du système climatique
Ch. 3
Le climat du futur
Se préparer à l'évaluation - Thème 1
Le futur des énergies
Ch. 4
Deux siècles d’énergie électrique
Ch. 5
Conversion et transport de l’énergie électrique
Ch. 6
Énergie, développement et futur climatique
Se préparer à l'évaluation - Thème 2
Une histoire du vivant
Ch. 7
La biodiversité et son évolution
Ch. 8
L’évolution comme grille de lecture du monde
Ch. 9
L’évolution humaine
Ch. 10
Les modèles démographiques
Ch. 11
De l’informatique à l’intelligence artificielle
Se préparer à l'évaluation - Thème 3
Livret maths
Fiches méthode
Esprit critique et scientifique
Améliorer ses compétences
Fiches histoire
Annexes
Ch. 10
Activité 2 - documentaire
Variation exponentielle de population
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Introduction
Les modèles affines ne sont pas les seuls à être utilisés pour décrire les
évolutions de population. Certaines peuvent être notamment modélisées
par des modèles exponentiels. La population est alors multipliée, à chaque
intervalle de temps, par un même facteur.
Problématique
Comment modéliser l'évolution d'un effectif par une suite géométrique ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Notation u(n)
- Puissance
- Représentations graphiques de courbes exponentielles
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Documents
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 1Population mondiale de 1950-1990 et de 2000-2020
| Année | Population mondiale | Variation relative (%) | Variation absolue |
|---|---|---|---|
| 1950 | 2 525 149 000 | ||
| 1955 | 2 758 315 000 | +9,23 | 233 166 000 |
| 1960 | 3 018 344 000 | +9,43 | 260 029 000 |
| 1965 | 3 322 495 000 | +10,08 | 304 151 000 |
| 1970 | 3 682 488 000 | +10,84 | 359 993 000 |
| 1975 | 4 061 399 000 | +10,29 | 378 911 000 |
| 1980 | 4 439 632 000 | +9,31 | 378 233 000 |
| 1985 | 4 852 541 000 | +9,30 | 412 909 000 |
| 1990 | 5 309 668 000 | +9,42 | 457 127 000 |
| Taux d'évolution sur la période | +9,34 | ||
| Année | Population mondiale | Variation relative (%) | Variation absolue |
|---|---|---|---|
| 2000 | 6 126 622 000 | ||
| 2005 | 6 519 636 000 | +6,41 | 393 014 000 |
| 2010 | 6 929 725 000 | +6,29 | 410 089 000 |
| 2015 | 7 349 472 000 | +6,06 | 419 747 000 |
| 2020 | 7 794 799 000 | +6,06 | 445 327 000 |
| Taux d'évolution sur la période | +6,06 | ||
Source : ONU (The World Population Prospects : the 2015 Revision)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 2Répartition et prévisions de la population
selon les régions du monde

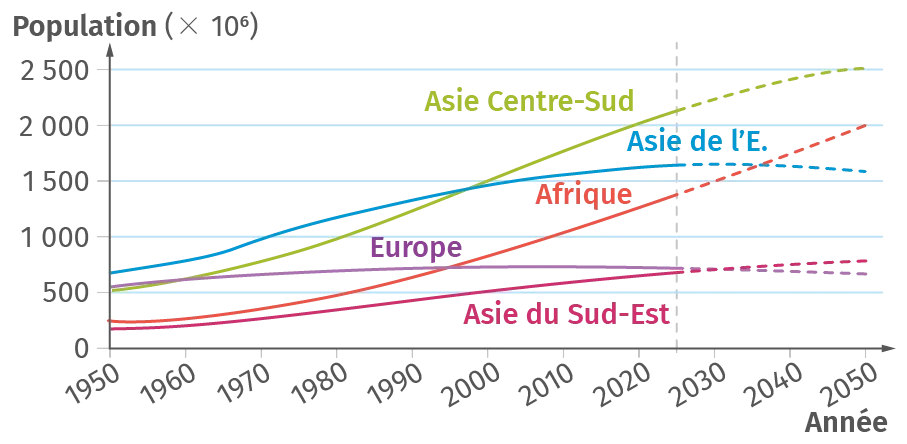
Évolution depuis 1950 et projection selon l'ONU jusqu'en 2050 de la population mondiale
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 3Croissance exponentielle
La croissance ou la décroissance d'une population est exponentielle
si celle-ci est multipliée par un même facteur à
chaque unité de temps. On peut la décrire à l'aide de la
variation relative (ou taux d'évolution) qui correspond à un
rapport constant :
On peut alors modéliser cette évolution par une suite géométrique, c'est-à-dire une suite dont le rapport entre deux termes consécutifs est constant, ou sous la forme :
u(n) = u(0) \cdot (1+t)^n \quad \Big| \quad u(0): \text{effectif initial}
\begin{array}{l|l}
t=\frac{u(n+1)-u(n)}{u(n)} & \begin{array}{l}
t: \text { variation relative ou taux } \\
\text { d'évolution } \\
u(n): \text { effectif à l'année } n
\end{array}
\end{array}
Si la variation relative par unité de temps est constante, alors la
population suit une croissance ou décroissance exponentielle.On peut alors modéliser cette évolution par une suite géométrique, c'est-à-dire une suite dont le rapport entre deux termes consécutifs est constant, ou sous la forme :
u(n) = u(0) \cdot (1+t)^n \quad \Big| \quad u(0): \text{effectif initial}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. Doc. 1 En comparant les évolutions de la variation
relative et de la variation absolue sur les deux
périodes 1950-1990 et 2000-2020, justifier que la
population mondiale suit plutôt une croissance
exponentielle.
2. Doc. 2 Identifier des régions du monde ne vérifiant
pas graphiquement ce type d'évolution.
3. Doc. 1 et Doc. 3 En vous basant sur le taux d'évolution
moyen entre 2000 et 2020, estimer :
- la population mondiale en 2050 et la comparer aux projections de l'ONU qui envisage 10 milliards d'êtres humains ;
- le nombre d'années nécessaires pour que la population mondiale double par rapport à celle de l'année 2000.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
