Enseignement scientifique Terminale - 2024

Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Sciences, climat et société
Ch. 1
L’atmosphère terrestre et la vie
Ch. 2
La complexité du système climatique
Ch. 3
Le climat du futur
Se préparer à l'évaluation - Thème 1
Le futur des énergies
Ch. 4
Deux siècles d’énergie électrique
Ch. 5
Conversion et transport de l’énergie électrique
Ch. 6
Énergie, développement et futur climatique
Se préparer à l'évaluation - Thème 2
Une histoire du vivant
Ch. 7
La biodiversité et son évolution
Ch. 8
L’évolution comme grille de lecture du monde
Ch. 9
L’évolution humaine
Ch. 10
Les modèles démographiques
Ch. 11
De l’informatique à l’intelligence artificielle
Se préparer à l'évaluation - Thème 3
Livret maths
Fiches méthode
Esprit critique et scientifique
Améliorer ses compétences
Fiches histoire
Annexes
Ch. 10
Enjeux scientifiques
Modèles d'évolution, simulations et limites
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La planète Terre fait face à une augmentation importante de la population humaine, ce qui provoque des bouleversements.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Néo-malthusianisme et limites planétaires
Sciences et société
Le néo-malthusianisme est une actualisation de la doctrine de Thomas Malthus qui promeut une limitation des naissances face à des ressources planétaires limitées. La maîtrise de la croissance démographique est proposée comme une solution de développement durable.
Les limites planétaires sont des seuils que l'humanité ne devrait pas dépasser pour maintenir la planète dans des conditions favorables à la vie humaine. Ce concept a été défini en 2009 au Stockholm Resilience Centre. D'après la dernière actualisation de 2023, six de ces neuf limites ont déjà été dépassées (schéma ci-contre).
Les limites planétaires sont des seuils que l'humanité ne devrait pas dépasser pour maintenir la planète dans des conditions favorables à la vie humaine. Ce concept a été défini en 2009 au Stockholm Resilience Centre. D'après la dernière actualisation de 2023, six de ces neuf limites ont déjà été dépassées (schéma ci-contre).

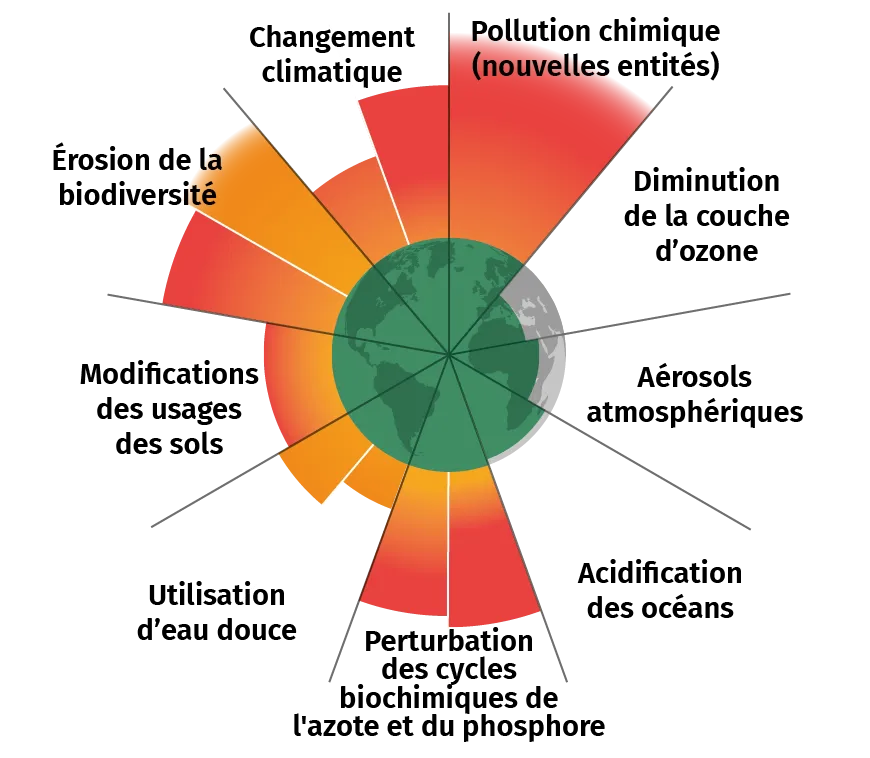
➜ Comment la limitation des naissances peut-elle participer à réduire l'intensité du changement climatique actuel ? Discuter des limites de cette solution.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Jeu de la vie - évolution d'une population et automate cellulaire
Sciences et société
Le jeu de la vie est un algorithme imaginé par le mathématicien britannique John Horton Conway en 1970. Cet algorithme fascine les mathématiciens et les informaticiens, mais aussi les biologistes et les philosophes, car il illustre le fait qu'un système suivant des règles simplistes peut générer des résultats extrêmement complexes.
L'algorithme se base sur un tableau de cases carrées, aussi grand qu'on le veut. Au départ, chacune des cases peut soit contenir une cellule vivante (case noire), soit ne rien contenir (case blanche). Ensuite, on fait évoluer la population de cellules selon l'état des cases voisines :
L'algorithme se base sur un tableau de cases carrées, aussi grand qu'on le veut. Au départ, chacune des cases peut soit contenir une cellule vivante (case noire), soit ne rien contenir (case blanche). Ensuite, on fait évoluer la population de cellules selon l'état des cases voisines :
- une case vide entourée par exactement trois cellules vivantes au tour n est occupée par une cellule vivante au tour n+1 ; si ce n'est pas le cas, elle reste vide ;
- une cellule vivante voisine de deux ou trois autres cellules vivantes au tour n reste vivante au tour n+1 ; si ce n'est pas le cas, elle meurt au tour n+1.



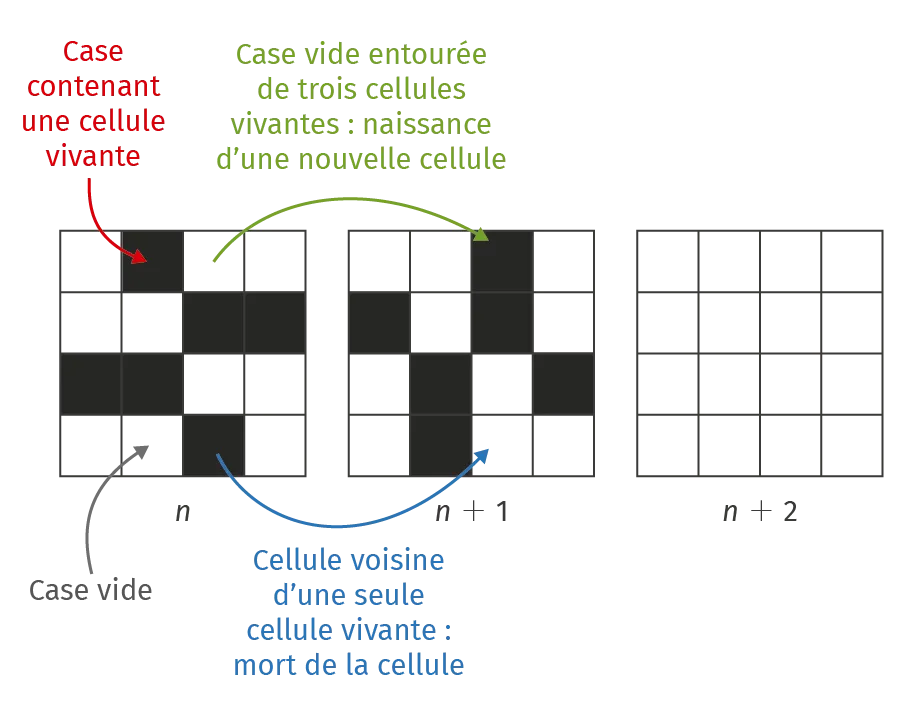
➜ Compléter l'étape suivante en suivant les règles du jeu de la vie. Ce motif s'appelle un oscillateur. D'après vous, pourquoi utilise-t-on ce terme ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retrouvez une version numérique du jeu de la vie.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
FocusDes modèles démographiques à la dynamique des populations Histoire des sciences
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La dynamique des populations est un domaine de l'écologie qui s'intéresse à la variation dans le temps de l'effectif d'une population d'êtres vivants. Un des objectifs de la dynamique des populations est de comprendre l'influence de l'environnement.
➜ Comment les modèles démographiques ont-ils mené aux modèles utilisés de nos jours en dynamique des populations ?
➜ Comment les modèles démographiques ont-ils mené aux modèles utilisés de nos jours en dynamique des populations ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
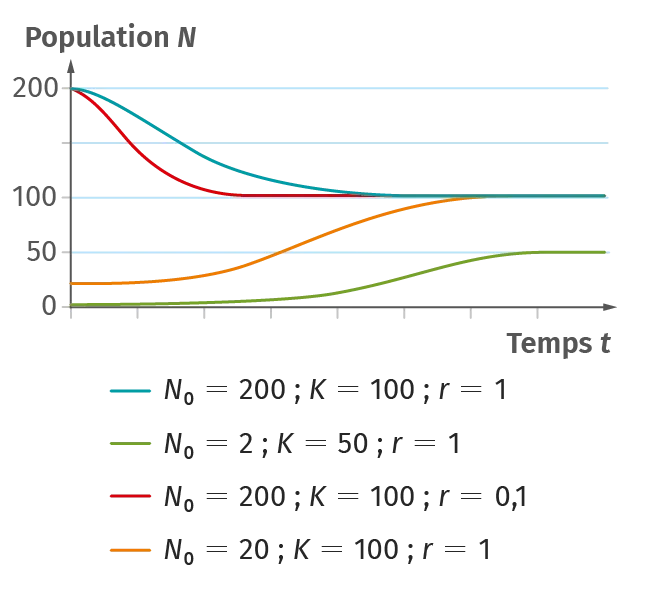
Doc. 1 Modèle logistique de Verhulst (1840)
Les modèles logistiques sont un premier raffinement des modèles malthusiens qui prennent en compte la capacité de charge du milieu K, c'est-à-dire l'effectif maximum qu'un milieu de vie peut supporter. En effet, de nombreux facteurs sont limitants dans un milieu de vie, par exemple le nombre de sites appropriés à la nidification, l'eau, la richesse du sol, le nombre de prédateurs, les abris adéquats et la quantité de nourriture.
\frac{\mathrm{d} N}{\mathrm{~d} t}=r \cdot N \cdot\left(1-\frac{N}{K}\right) \left\lvert\, \begin{aligned} & \frac{\mathrm{d} N}{\mathrm{~d} t}: \text { dérivée par rapport au temps de la taille } \\ & \text { de population } \\ & N: \text { taille de population à l'instant } t \\ & t: \text { temps } \\ & r: \text { croissance intrinsèque de la population } \\ & K: \text { capacité de charge du milieu } \\ & N_{0}: \text { taille de population initiale } \end{aligned}\right.
\frac{\mathrm{d} N}{\mathrm{~d} t}=r \cdot N \cdot\left(1-\frac{N}{K}\right) \left\lvert\, \begin{aligned} & \frac{\mathrm{d} N}{\mathrm{~d} t}: \text { dérivée par rapport au temps de la taille } \\ & \text { de population } \\ & N: \text { taille de population à l'instant } t \\ & t: \text { temps } \\ & r: \text { croissance intrinsèque de la population } \\ & K: \text { capacité de charge du milieu } \\ & N_{0}: \text { taille de population initiale } \end{aligned}\right.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
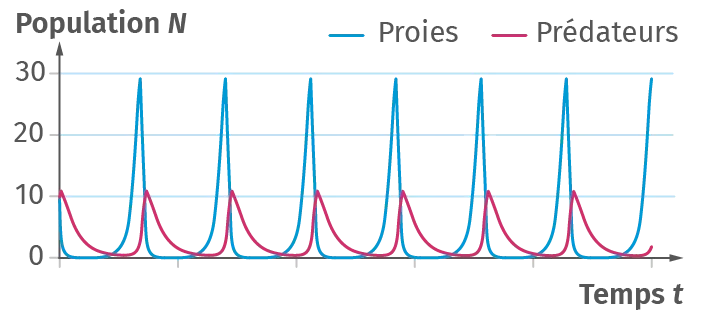
Doc. 2 Modèle proie-prédateur de Lotka-Volterra (1925-1926)
Les équations de prédation de Lotka et Volterra sont utilisées pour décrire la dynamique d'un système biologique dans lequel des prédateurs et des proies interagissent. En absence de prédation, le modèle de Lotka-Volterra prédit une croissance exponentielle des proies. Les prédateurs, quant à eux, ont une décroissance exponentielle en l'absence de proie.

\begin{array}{c|c}
\begin{gathered}
\frac{\mathrm{d} N_{\text {proies }}}{\mathrm{d} t}=\alpha \cdot N_{\text {proies }}-\beta \cdot N_{\text {proies }} \cdot N_{\text {prédateurs }} \\
\frac{\mathrm{d} N_{\text {prédateurs }}}{\mathrm{d} t}=\delta \cdot N_{\text {proies }} \cdot N_{\text {prédateurs }}-\gamma \cdot N_{\text {prédateurs }}
\end{gathered}
&
\begin{gathered}
\alpha : \text{taux de reproduction des proies} \\
\beta : \text{taux de mortalité des proies dû aux prédateurs} \\
\delta : \text{taux de reproduction des prédateurs en fonction des proies}\\ \text{rencontrées et mangées} \\
\gamma : \text{taux de mortalité des prédateurs}
\end{gathered}
\end{array}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
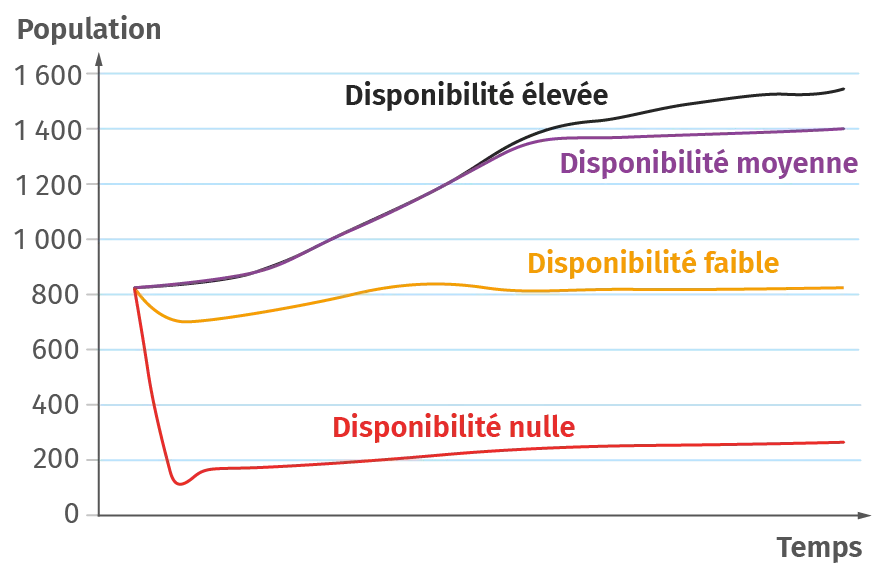
Doc. 3 Dynamique des populations et conservation
Le vautour fauve est un oiseau nécrophage emblématique
des Grands Causses, ensemble de hauts plateaux calcaires, au sud du Massif central. Disparus du massif dans les années 1940, les vautours fauves ont été réintroduits depuis 1981. Mais une interdiction datant de 2003 met en danger la survie de ces oiseaux. En effet, suite à la crise de la vache folle, les charniers à ciel ouvert sont désormais interdits pour des raisons sanitaires. Le graphique ci-contre modélise la dynamique de la population de vautours fauves
Disponibilité nulle
en fonction de la disponibilité de carcasses d'animaux sauvages et d'élevages.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
À l'oral
À l'aide de vos connaissances, discuter de l'intérêt et des limites des modèles ci-dessus.
Cliquez pour accéder à un module d'enregistrement audio
Enregistreur audio
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
