Enseignement scientifique Terminale - 2024

Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Sciences, climat et société
Ch. 1
L’atmosphère terrestre et la vie
Ch. 2
La complexité du système climatique
Ch. 3
Le climat du futur
Se préparer à l'évaluation - Thème 1
Le futur des énergies
Ch. 4
Deux siècles d’énergie électrique
Ch. 5
Conversion et transport de l’énergie électrique
Ch. 6
Énergie, développement et futur climatique
Se préparer à l'évaluation - Thème 2
Une histoire du vivant
Ch. 7
La biodiversité et son évolution
Ch. 8
L’évolution comme grille de lecture du monde
Ch. 9
L’évolution humaine
Ch. 10
Les modèles démographiques
Ch. 11
De l’informatique à l’intelligence artificielle
Se préparer à l'évaluation - Thème 3
Livret maths
Fiches méthode
Esprit critique et scientifique
Améliorer ses compétences
Fiches histoire
Annexes
Ch. 10
Cours
Les modèles démographiques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Modèle d'évolution linéaire
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
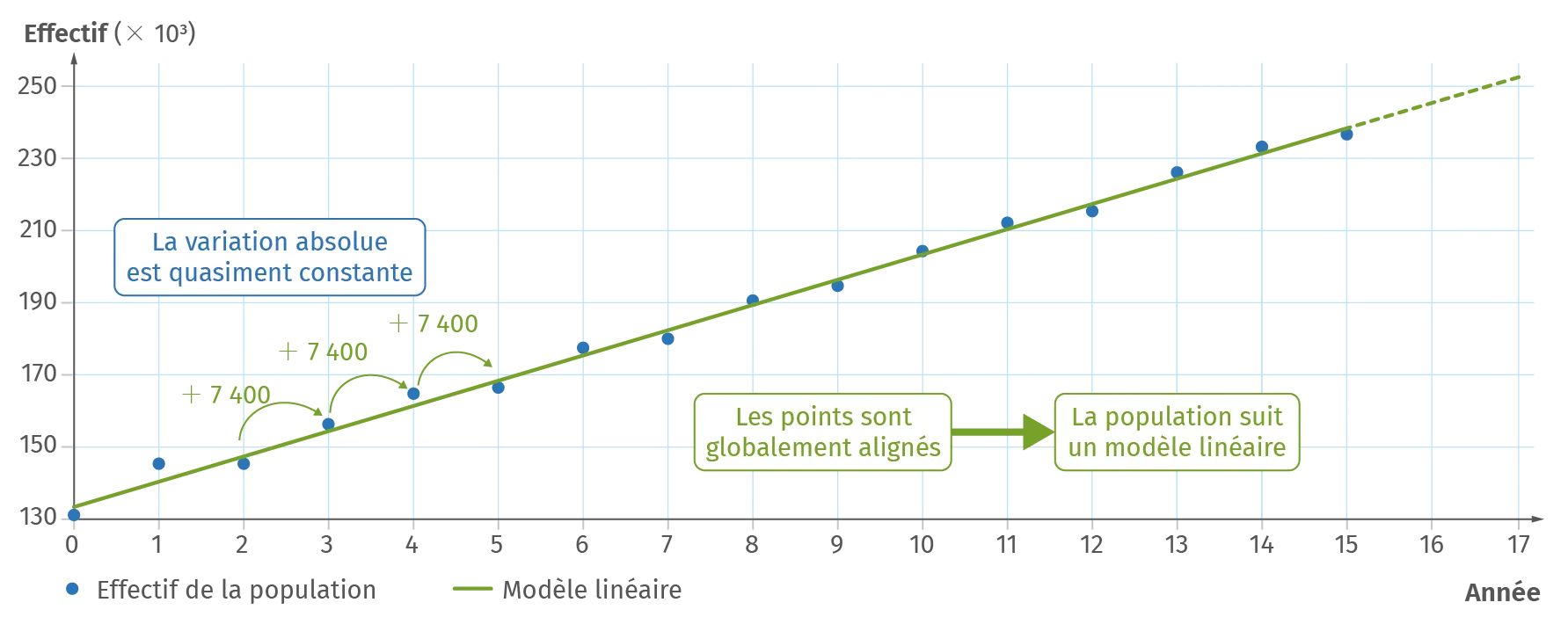
A Variation absolue
- Il est possible de modéliser l'évolution d'une population par un modèle linéaire lorsque la variation absolue de la population par unité de temps est constante, c'est-à-dire que la population augmente ou diminue du même nombre d'individus par unité de temps. En représentant l'évolution de cette population en fonction du temps, le nuage de points montre un alignement des points.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
B Suite arithmétique
- Ce type de modèle peut être décrit à l'aide d'une suite arithmétique u. Il existe un nombre réel, appelé raison, tel que pour tout entier naturel n :
- Ainsi, en connaissant le recensement initial de la population u(0) et la raison r, on peut prédire la population au temps n avec la formule :
u(n+1)=u(n)+r
u(n)=u(0)+n \cdot r
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2 Modèle d'évolution exponentiel
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
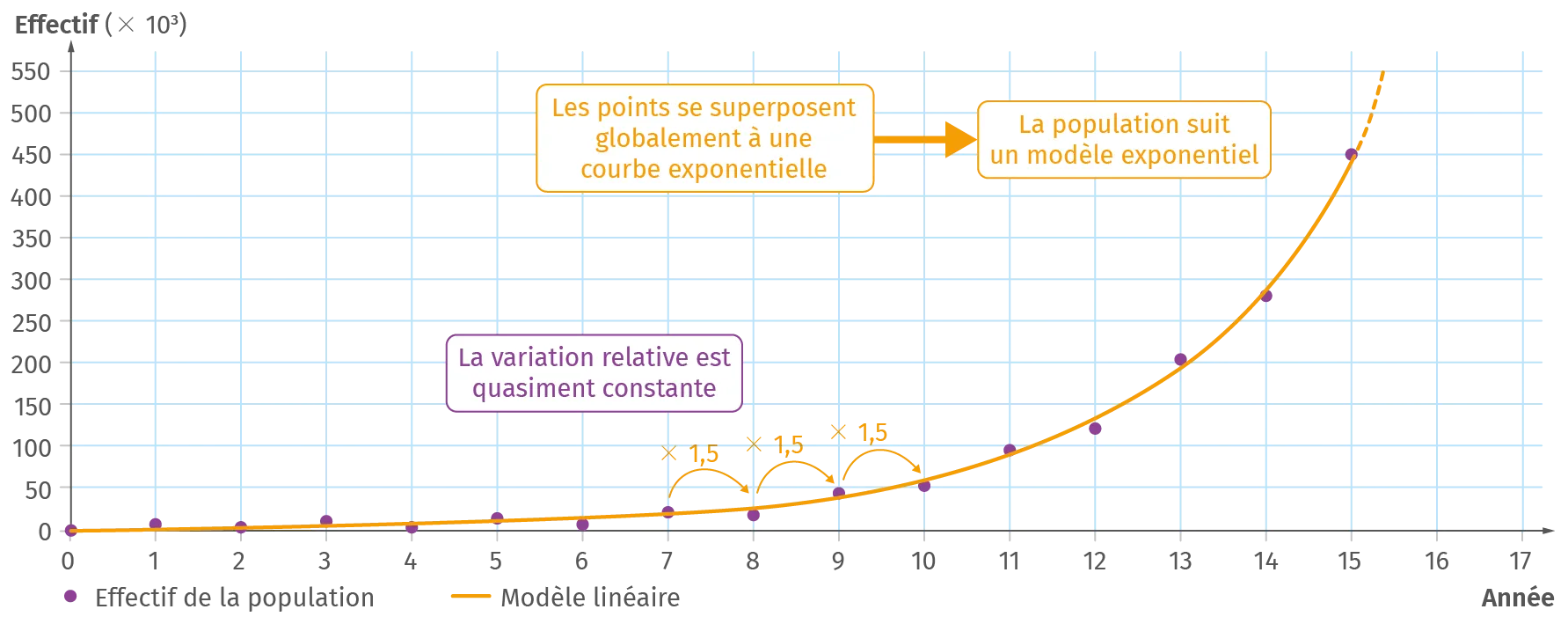
A Variation relative
- Lorsque l'évolution d'une population augmente ou décroît avec une variation relative constante, cela signifie que la population est multipliée ou divisée par un même facteur à chaque unité de temps. En représentant l'effectif de cette population en fonction du temps, la courbe représentative correspond à une courbe de type exponentielle.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
B Suite géométrique
- Le modèle exponentiel peut être décrit par une suite géométrique u pour laquelle passer d'un terme au suivant revient à multiplier toujours par un même nombre réel q, appelé raison. Ce nombre, associé à la variation relative (ou taux d'évolution) t d'une population, est égal à {q=1+t}.
- La suite géométrique qui décrit l'évolution de la population correspond alors à :
u(n+1)=u(n) \cdot q
u(n+1)=u(n) \cdot(1+t) - Ainsi, en connaissant l'effectif initial u(0) et le taux d'évolution de la population t, il est possible de prédire l'effectif d'une population au temps n :
u(n)=u(0) \cdot(1+t)^n
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
C Modèle démographique de Malthus
- Malthus s'est appuyé sur les évolutions des modèles géométriques pour prévoir l'évolution d'une population à partir du taux d'évolution t, qu'il a associé à la différence entre le taux de natalité t_{nat} et le taux de mortalité t_{mor}. Son modèle, valable sur des temps courts, pose la question du déséquilibre futur entre la population et les ressources disponibles.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Taux de mortalité : rapport entre le nombre annuel de décès et la population d'un territoire.
- Taux de natalité : rapport entre le nombre annuel de naissances et la population d'un territoire.
- Taux d'évolution : variation relative d'un effectif de population entre deux instants.
- Variation absolue : écart entre les valeurs u_{n+1} et u_n.
- Variation relative : rapport entre la variation absolue u_{n+1}-u_n et la valeur u_n.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les modèles les plus élaborés prévoient que la population mondiale atteindra environ 10 milliards d'êtres humains en 2050.
L'ONU estime que la population mondiale a atteint le seuil de 8 milliards d'individus fin 2022.
L'ONU estime que la population mondiale a atteint le seuil de 8 milliards d'individus fin 2022.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les évolutions de population abordées dans ce chapitre sont des modèles théoriques et simplifiés. Les évolutions réelles de population sont toujours plus complexes et nécessitent que l'on ne s'intéresse qu'à des durées limitées.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
En mathématiques, la raison est la valeur qui permet de passer du terme de rang n au terme de rang n+1 dans les suites arithmétiques et géométriques. Ici, la raison de la suite arithmétique est r, et la raison de la suite géométrique est q = 1 + t.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Modèle linéaire
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Modèle exponentiel
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
