Méthode d'Euler

Soit f la fonction définie sur \R par f(x)=\frac{1}{1+x^{2}}.
On souhaite approcher par la méthode d'Euler la primitive \text{F} de f vérifiant \text{F}(0) = 0.
On choisit de représenter \text{F} sur \text{I} = [0 \:; 2].
On commence par choisir un pas h > 0. On pose x_0 = 0 et, pour tout entier naturel n, x_{n+1} = x_n + h, puis on définit les points \text{M}(x_n \:; y_n) proches de la courbe représentative de \text{F.}


1. Exprimer x_1 en fonction de h.

2. Justifier que y_0 = 0.

3. En utilisant l'approximation \mathrm{F}(a+h) \approx \mathrm{F}(a)+h \times f(a) avec h proche de 0 et a appartenant à \text{I,} exprimer y_1 en fonction de h.

Construire sur \boldsymbol{[0 \:; 2]}, point par point avec la méthode d'Euler, une approximation de la courbe représentative de la solution d'un problème du type \boldsymbol{y}^{\prime}(\boldsymbol{x})=\boldsymbol{f}(\boldsymbol{x}) et \boldsymbol{y}\left(\boldsymbol{x}_\boldsymbol{0}\right)=\boldsymbol{y}_\boldsymbol{0}, en utilisant une des deux méthodes.

Dans une feuille de calcul, on construit un tableau donnant les valeurs de x_n et y_n, où n est un entier naturel de 0 à 20.
On entre la valeur 0 dans la cellule B2, la valeur 0 dans la cellule C2 et on choisit pour pas h = 0{,}1.
On obtient alors la feuille de calcul suivante.


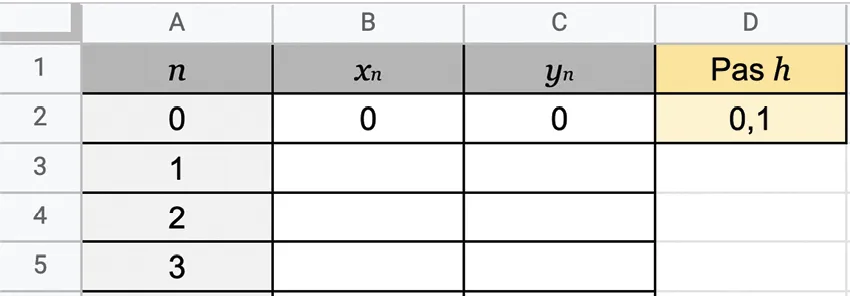
1. Quelles formules doit-on saisir dans les cellules B3 et C3, puis étirer vers le bas, pour obtenir les valeurs sucessives de x_n et de y_n ?

2. Représenter le nuage de points \text{M}(x_n \:; y_n).

On donne ci‑après un programme en langage Python qui permet d'afficher une approximation de la courbe représentative de \text{F} sur l'intervalle \text{I} = [0\: ; 2].

1. Que représente y_0 ?

2. Compléter la ligne 4 du programme.

3. Que représentent les variables \color{purple}\bf{h} et \color{purple}\bf{n} ?

4. Compléter le programme dans la boucle \color{purple}\bf{for} pour afficher une approximation de la courbe représentative de \text{F} sur l'intervalle \text{I} = [0 \:; 2].

5. Afficher cette approximation de la courbe représentative de \text{F} sur l'intervalle \text{I} = [0 \:; 2] pour n = 1\:000.

from matplotlib.pyplot import *

def f(x):
  return ...

def Euler(fonctionf, x0, y0, xf, n):
  x = x0
  y = y0
  X = [x]
  Y = [y]
  h = (xf-x0)/n
  for i in range(n):
    x = x + h
    y = ...
    X.append(x)
    Y.append(y)
  plot(X, Y, 'ro')
  grid()
  show()

En complément du nuage de points représenté, faire apparaître la courbe représentative de la fonction arctangente définie sur \R par x \mapsto \arctan (x) (fonction ATAN sur Excel ou arctan de la bibliothèque Python numpy).

Quelle conjecture peut‑on émettre ?