Mathématiques 1re Techno
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Analyse
Ch. 1
Suites
Ch. 2
Fonctions
Ch. 3
Dérivation
Partie 2 : Statistiques et probabilités
Ch. 4
Fréquences conditionnelles et probabilités conditionnelles
Ch. 5
Variables aléatoires
Automatismes
Partie 3 : Géométrie
Ch. 6
Trigonométrie
Ch. 7
Produit scalaire
Ch. 8
Nombres complexes
Partie 4 : Analyse
Ch. 9
Compléments sur la dérivation
Ch. 10
Primitives
Révisions Genially
Chapitre 11
Entraînement 2
Calcul de primitives
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 74
[Calculer.]
Exercice 74
[Calculer.]
Dans chaque cas, déterminer une primitive de la fonction donnée sur \R.
1. f: x \mapsto 44 \sin (x)
2. g: x \mapsto x-6
3. h: x \mapsto 3 x+56
4. k: x \mapsto x^{2}+1
1. f: x \mapsto 44 \sin (x)
2. g: x \mapsto x-6
3. h: x \mapsto 3 x+56
4. k: x \mapsto x^{2}+1
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 75
[Calculer.]
Exercice 75
[Calculer.]
Dans chaque cas, déterminer toutes les primitives de la fonction donnée sur \R.
1. f: x \mapsto 2021
2. g: x \mapsto x+1
3. h: x \mapsto x^2-1
4. k: x \mapsto x^{3}-2 x^{2}+4 x
1. f: x \mapsto 2021
2. g: x \mapsto x+1
3. h: x \mapsto x^2-1
4. k: x \mapsto x^{3}-2 x^{2}+4 x
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 76
[Calculer.]
Exercice 76
[Calculer.]
Dans chaque cas, déterminer toutes les primitives de la fonction donnée sur \R.
1. f: x \mapsto x^{4}-3 x^{3}+5 x^{2}+5 x
2. g: x \mapsto \frac{3 x^{3}}{2}+\frac{x^{2}}{4}+9 x
3. h: x \mapsto \frac{3 x^{4}}{2}+\frac{5 x^{2}}{6}+10
4. k: x \mapsto \frac{4 x^{5}}{3}+\frac{-2 x}{3}-10
1. f: x \mapsto x^{4}-3 x^{3}+5 x^{2}+5 x
2. g: x \mapsto \frac{3 x^{3}}{2}+\frac{x^{2}}{4}+9 x
3. h: x \mapsto \frac{3 x^{4}}{2}+\frac{5 x^{2}}{6}+10
4. k: x \mapsto \frac{4 x^{5}}{3}+\frac{-2 x}{3}-10
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 77
[Calculer.]
Exercice 77
[Calculer.]
Dans chaque cas, déterminer toutes les primitives
de la fonction donnée sur \R.
1. f: x \mapsto \cos (6 x+9)
2. g: x \mapsto \sin (6 x-7)
3. h: x \mapsto \frac{3 x^{3}}{2}+\frac{x}{2}
4. k: x \mapsto \frac{3 x^{4}}{2}+\frac{x^{3}}{5}-7 x
1. f: x \mapsto \cos (6 x+9)
2. g: x \mapsto \sin (6 x-7)
3. h: x \mapsto \frac{3 x^{3}}{2}+\frac{x}{2}
4. k: x \mapsto \frac{3 x^{4}}{2}+\frac{x^{3}}{5}-7 x
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 78
[Calculer.]
Exercice 78
[Calculer.]
Dans chaque cas, déterminer toutes les primitives de la fonction donnée sur \R.
1. f: x \mapsto \frac{-5 x^{4}}{2}+\frac{x^{2}}{7}-8 x
2. g: x \mapsto \cos (4 x+3)
3. h: x \mapsto \sin (x+9)
4. k: x \mapsto-\sin (6 x+7)
1. f: x \mapsto \frac{-5 x^{4}}{2}+\frac{x^{2}}{7}-8 x
2. g: x \mapsto \cos (4 x+3)
3. h: x \mapsto \sin (x+9)
4. k: x \mapsto-\sin (6 x+7)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 79
[Calculer.]
Exercice 79
[Calculer.]
Dans chaque cas, déterminer toutes les primitives de la fonction donnée sur l'intervalle \text{I.}
1. f: x \mapsto-\sin (8 x-4)+x^{3}-\frac{9 x}{2} sur \mathrm{I}=\mathbb{R}.
2. g: x \mapsto 2 \cos (5 x-3)+x^{3}+\frac{7 x}{4} sur \mathrm{I}=\mathbb{R}.
1. f: x \mapsto-\sin (8 x-4)+x^{3}-\frac{9 x}{2} sur \mathrm{I}=\mathbb{R}.
2. g: x \mapsto 2 \cos (5 x-3)+x^{3}+\frac{7 x}{4} sur \mathrm{I}=\mathbb{R}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 80
[Calculer.]
Exercice 80
[Calculer.]
Dans chaque cas, déterminer toutes les primitives
de la fonction donnée sur l'intervalle \text{I} considéré.
1. f: x \mapsto 3 \cos (7 x)+\sin (5 x-3) sur \mathrm{I}=\mathbb{R}.
2. g: x \mapsto-4 \sin (8 x-9)-2 \cos \left(\frac{5 x}{4}-2\right) sur \mathrm{I}=\mathbb{R}.
1. f: x \mapsto 3 \cos (7 x)+\sin (5 x-3) sur \mathrm{I}=\mathbb{R}.
2. g: x \mapsto-4 \sin (8 x-9)-2 \cos \left(\frac{5 x}{4}-2\right) sur \mathrm{I}=\mathbb{R}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 81
[Calculer.]
Exercice 81
[Calculer.]
Dans chaque cas, déterminer toutes les primitives
de la fonction donnée sur l'intervalle \text{I} considéré.
1. f: x \mapsto \cos (6 x+\pi) sur \mathrm{I}=\mathbb{R}.
2. g: x \mapsto 2 \sin \left(2 x+\frac{\pi}{4}\right) sur \mathrm{I}=\mathbb{R}.
1. f: x \mapsto \cos (6 x+\pi) sur \mathrm{I}=\mathbb{R}.
2. g: x \mapsto 2 \sin \left(2 x+\frac{\pi}{4}\right) sur \mathrm{I}=\mathbb{R}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 82
[Calculer.]
Exercice 82
[Calculer.]
Déterminer la primitive \text{F} de la fonction f sur \R définie
par f(x) = 6x + 2 et vérifiant \text{F}(1) = 2.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 83
[Calculer.]
Exercice 83
[Calculer.]
Déterminer la primitive \text{F} de f sur \R définie par
f(x)=\frac{5 x^{2}}{8}-3 x+2 et vérifiant \text{F}(-1) = 2.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 84
[Calculer.]
Exercice 84
[Calculer.]
Déterminer la primitive \text{G} de g sur \R définie par g(x)=\frac{2 x^{3}+3 x^{2}+9}{5} et vérifiant \mathrm{G}(1)=1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 86
[Calculer.]
Exercice 86
[Calculer.]
Déterminer la primitive \text{F} de f sur \R définie par
f(x) = 4\sin(2x) - 3\sin(5x) et vérifiant \text{F}(\pi) = 0.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 85
[Calculer.]
Exercice 85
[Calculer.]
Dans chaque cas, déterminer la primitive \text{F} de f sur \R qui s'annule en x = -1.
1. f(x)=9 x^{2}-\frac{3 x}{5}
2. f(x)=8 x^{3}-10 x^{2}-7 x
3. f(x)=\frac{3 x^{4}}{2}-10 x+1
1. f(x)=9 x^{2}-\frac{3 x}{5}
2. f(x)=8 x^{3}-10 x^{2}-7 x
3. f(x)=\frac{3 x^{4}}{2}-10 x+1
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 87
[Communiquer.]
Exercice 87
[Communiquer.]
Un logiciel de calcul formel donne le résultat suivant lorsqu'on lui demande de déterminer une primitive de x \mapsto \frac{5 x^{4}}{3}+2 x^{2}.

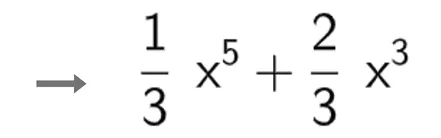
Vérifier la réponse obtenue.

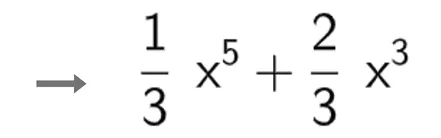
Vérifier la réponse obtenue.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 88
[Chercher.]
Exercice 88
[Chercher.]
Déterminer les primitives de la fonction f définie pour tout réel x par f(x) = (4x + 7)(-2x + 3).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 89
[Chercher.]
Exercice 89
[Chercher.]
Déterminer les primitives sur l'intervalle \text{I} indiqué des fonctions suivantes.
1. f(x)=\left(2 x^{2}-3 x+2\right)(-2 x+1) sur \mathrm{I}=\mathbb{R}.
2. g(x)=\frac{x^{3}-3 x^{2}+2 x}{x} sur \mathrm{I}=[1 \:; 10]
3. h(x)=5\left(3 x^{2}+2 x+3\right) sur \mathrm{I}=\mathbb{R}.
1. f(x)=\left(2 x^{2}-3 x+2\right)(-2 x+1) sur \mathrm{I}=\mathbb{R}.
2. g(x)=\frac{x^{3}-3 x^{2}+2 x}{x} sur \mathrm{I}=[1 \:; 10]
3. h(x)=5\left(3 x^{2}+2 x+3\right) sur \mathrm{I}=\mathbb{R}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 90
[Raisonner.]
Exercice 90
[Raisonner.]
Déterminer une expression possible d'une primitive \text{F} d'une fonction f polynôme de degré 2 dont le tableau de variations correspond à celui ci‑dessous.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 91
[Communiquer.]
Exercice 91
[Communiquer.]
Dans un exercice, on cherche à déterminer les primitives
de la fonction f définie sur \R par :
Voici la production d'un élève.
Cette production comporte plusieurs erreurs. Les retrouver, puis répondre au problème initial.
f(x)=\left(3 x^{2}-2 x+1\right)(2 x+3).
Voici la production d'un élève.
On intègre terme à terme.
Les primitives \text{F} de f sont définies sur \mathbb{R} par \text{F}(x)=\left(x^{3}-x^{2}+x+k\right)\left(x^{2}+3 x+k\right) où k \in \mathbb{R}.
Les primitives \text{F} de f sont définies sur \mathbb{R} par \text{F}(x)=\left(x^{3}-x^{2}+x+k\right)\left(x^{2}+3 x+k\right) où k \in \mathbb{R}.
Cette production comporte plusieurs erreurs. Les retrouver, puis répondre au problème initial.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 92
[Représenter.]
Exercice 92
[Représenter.]
Dans chaque cas, représenter, dans un repère orthogonal, la primitive \text{F} de la fonction f définie sur \R par :
1. f(x)=9 x^{2}-7 x+5 et vérifiant \mathrm{F}(1)=0.
2. f(x)=5 x^{3}+6 x-10 et vérifiant \mathrm{F}(0)=0.
1. f(x)=9 x^{2}-7 x+5 et vérifiant \mathrm{F}(1)=0.
2. f(x)=5 x^{3}+6 x-10 et vérifiant \mathrm{F}(0)=0.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 93
[Raisonner.]
Exercice 93
[Raisonner.]
Une particule se déplace sans frottement et sans vitesse initiale le long d'un axe horizontal de repère (\mathrm{O} \:; \vec{i}) à partir du point \text{O.} Son accélération instantanée, en m/s2, est donnée à l'instant t, en seconde, pour t \in[0 \:; 180], par a(t)=\cos \left(3 t+\frac{\pi}{2}\right).
1. Déterminer, pour tout t \in[0 \:; 180], la vitesse instantanée v(t), en m/s, de la particule.
2. Exprimer, pour tout t \in[0 \:; 180], l'abscisse x(t), en mètre, de la particule à l'instant t.
1. Déterminer, pour tout t \in[0 \:; 180], la vitesse instantanée v(t), en m/s, de la particule.
2. Exprimer, pour tout t \in[0 \:; 180], l'abscisse x(t), en mètre, de la particule à l'instant t.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 95
[Raisonner.]
Exercice 95
[Raisonner.]
La réaction d'oxydation des ions iodures par l'eau
oxygénée est donnée par l'équation chimique :
Avec un volume \text{V} = 0{,}1 L, la vitesse volumique de formation du diiode \text{I}_2 à l'instant t est donnée par :
Déterminer l'expression de x(t) à l'instant t. On choisira x(0) = 0.
2 \mathrm{I}^{-}+\mathrm{H}_{2} \mathrm{O}_{2}+2 \mathrm{H}^{+} \rightarrow \mathrm{I}_{2}+2 \mathrm{H}_{2} \mathrm{O}.
La vitesse volumique de formation du diiode \text{I}_2,
à l'instant t, est égale à v(t)=\frac{x^{\prime}(t)}{\mathrm{V}}, où \text{V} désigne le volume du mélange réactionnel et x(t) l'avancement molaire du diiode, en mol, à l'instant t \in[0 \:; 400], en seconde.Avec un volume \text{V} = 0{,}1 L, la vitesse volumique de formation du diiode \text{I}_2 à l'instant t est donnée par :
v(t)=0{,}0006 t^{2}+0{,}75 t+0{,}44.
Déterminer l'expression de x(t) à l'instant t. On choisira x(0) = 0.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 94
[Raisonner.]
Exercice 94
[Raisonner.]


Un champion de moto démarre sa course sans vitesse initiale et avec une accélération, en m/s2, donnée pendant 1{,}5 secondes par a(t) = 10t^2 + 3t, où t désigne le temps écoulé en seconde depuis le début de sa course, avec t \in [0 \: ; 1{,}5].
1. Déterminer, en fonction de t, l'expression de la fonction v, représentant la vitesse instantanée de cette moto, en m/s, et primitive de a sur [0 \: ; 1{,}5].
2. Exprimer, pour tout t \in [0 \: ; 1{,}5], la distance x(t) parcourue par le champion de moto, en mètre, en choisissant x(0) = 0.
3. Quelle distance aura parcouru le champion de moto pendant la première seconde et demie de sa course ?
Dans la vie professionnelle
Les bacheliers technologiques peuvent accéder à de multiples formations du supérieur leur permettant notamment d'intégrer des écoles d'ingénieurs. Parmi ces écoles, certaines forment aux métiers de la mécanique (secteur automobile, aéronautique, cabinets d'étude). Les tâches sont nombreuses : conception de prototypes, tests et propositions d'améliorations font partie des responsabilités possibles.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 96
[Raisonner.]
Exercice 96
[Raisonner.]
Pour s'entraîner pour sa prochaine compétition, Hakim s'entraîne au plongeon. On note y(t) la position d'Hakim à l'instant t \in [0\: ; 5], en seconde, sur un axe dirigé vers le bas. Avant son plongeon, Hakim est situé à 10 m (origine de l'axe vertical) de la surface de l'eau. Il saute du plongeoir sans vitesse initiale, il subit une accélération constante g = 9{,}81 m/s2.
1. Déterminer sa vitesse v(t), puis la position y(t) de Hakim à l'instant t.
2. À quel instant t Hakim se trouvera‑t‑il à 2 m de la surface de l'eau ? Quelle sera alors sa vitesse en m/s ? En km/h ?


1. Déterminer sa vitesse v(t), puis la position y(t) de Hakim à l'instant t.
2. À quel instant t Hakim se trouvera‑t‑il à 2 m de la surface de l'eau ? Quelle sera alors sa vitesse en m/s ? En km/h ?


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 97
[Raisonner.]
Exercice 97
[Raisonner.]
Assis dans son jardin, Isaac observe la chute d'une pomme de son pommier. Soucieux de comprendre cette trajectoire, il utilise les lois de Newton.
Il admet que seule la force du poids s'applique sur la pomme. Il obtient que l'accélération instantanée a(t) de la pomme à l'instant t est constante et vaut a(t) = -9{,}8 m/s2.
On admet que la pomme tombe d'une hauteur de 2{,}5 m et sans vitesse initiale à l'instant t = 0 et on choisit 0 la hauteur du sol.
1. Calculer, pour tout t, la position x(t) de la pomme.
2. Calculer au bout de combien de temps la pomme atteint le sol. On arrondira le résultat à 0{,}1 s.
Il admet que seule la force du poids s'applique sur la pomme. Il obtient que l'accélération instantanée a(t) de la pomme à l'instant t est constante et vaut a(t) = -9{,}8 m/s2.
On admet que la pomme tombe d'une hauteur de 2{,}5 m et sans vitesse initiale à l'instant t = 0 et on choisit 0 la hauteur du sol.
1. Calculer, pour tout t, la position x(t) de la pomme.
2. Calculer au bout de combien de temps la pomme atteint le sol. On arrondira le résultat à 0{,}1 s.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 98
Exercice inversé
Exercice 98
Exercice inversé
En réponse à un exercice, on écrit : « \text{F}(x) = 4x^3 + 6x - 2 ».
Rédiger un énoncé possible de cet exercice.
Rédiger un énoncé possible de cet exercice.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 99
Exercice inversé
Exercice 99
Exercice inversé
En réponse à un exercice, on écrit : « Pour une durée de vol t \in[0 \:; 15], la distance, en km, parcourue par l'avion s'exprime, en fonction de t, en heure, par x(t)=-0{,}5 t^{3}+25 t^{2}+210 t ».
Rédiger un énoncé possible de cet exercice.
Rédiger un énoncé possible de cet exercice.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
