Chapitre 11
Entraînement 3
La méthode d'Euler
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 100
Tableur
[Représenter.]
Soit f la fonction définie sur \text{I} = [1 \:; 5] par f(x)=\frac{1}{x}.
À l'aide de la méthode d'Euler, on cherche à déterminer de manière approchée la primitive \text{F} de f vérifiant \text{F}(1) = 0. On choisit pour cela un pas h = 0{,}2.
1. En choisissant h = 0{,}2, combien de points allons‑nous obtenir ?
2. Quelle formule doit‑on entrer, puis étendre dans la cellule D2, pour compléter la colonne D de la feuille de calcul ci‑dessous ?
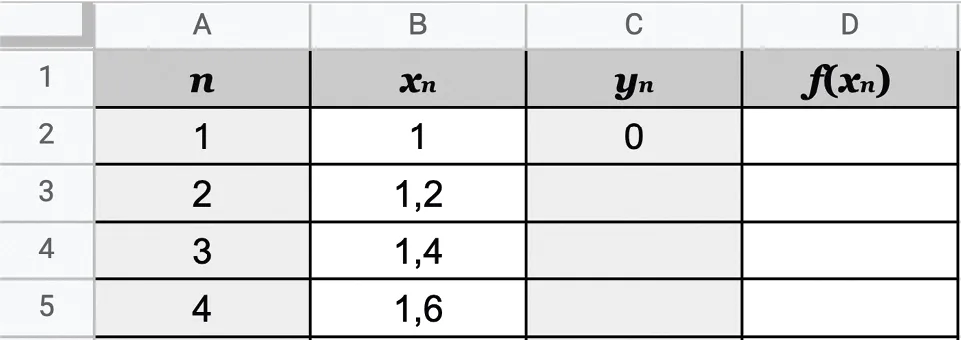
3. En utilisant l'approximation affine donnée par \mathrm{F}(a+h) \approx \mathrm{F}(a)+h \times f(a), donner la formule à entrer et étendre dans la cellule C3 pour compléter la colonne C de la feuille de calcul ci‑dessus.
4. Afficher le nuage de points approchant la courbe représentative de la fonction y.
5. En complément du nuage de points représenté, utiliser le tableur pour faire apparaître la courbe de la fonction logarithme népérien définie sur ] 0\: ;+\infty[ par x \mapsto \ln (x). Quelle conjecture peut‑on émettre ?
À l'aide de la méthode d'Euler, on cherche à déterminer de manière approchée la primitive \text{F} de f vérifiant \text{F}(1) = 0. On choisit pour cela un pas h = 0{,}2.
1. En choisissant h = 0{,}2, combien de points allons‑nous obtenir ?
2. Quelle formule doit‑on entrer, puis étendre dans la cellule D2, pour compléter la colonne D de la feuille de calcul ci‑dessous ?
3. En utilisant l'approximation affine donnée par \mathrm{F}(a+h) \approx \mathrm{F}(a)+h \times f(a), donner la formule à entrer et étendre dans la cellule C3 pour compléter la colonne C de la feuille de calcul ci‑dessus.
4. Afficher le nuage de points approchant la courbe représentative de la fonction y.
5. En complément du nuage de points représenté, utiliser le tableur pour faire apparaître la courbe de la fonction logarithme népérien définie sur ] 0\: ;+\infty[ par x \mapsto \ln (x). Quelle conjecture peut‑on émettre ?
Histoire des maths
Né à Bâle le 15 avril 1707, Leonhard Euler étudie les mathématiques sur les conseils de Johann Bernoulli, un ami de son père.
Il s'intéresse à toutes les branches des mathématiques avant de mourir à Saint‑Pétersbourg en 1783, à l'âge de 76 ans. Euler fonde ce qu'on appelle aujourd'hui l'analyse fonctionnelle, en donnant une définition précise de la notion de fonction.
Il s'intéresse à toutes les branches des mathématiques avant de mourir à Saint‑Pétersbourg en 1783, à l'âge de 76 ans. Euler fonde ce qu'on appelle aujourd'hui l'analyse fonctionnelle, en donnant une définition précise de la notion de fonction.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 101
Tableur
[Représenter.]
Soit f la fonction définie sur [1\: ; 10] par f(x)=\frac{1}{\sqrt{x}}.
On cherche à approcher, en utilisant la méthode d'Euler, la primitive de f \operatorname{sur}[1 \:; 10] vérifiant \mathrm{F}(1)=2.
1. À l'aide d'une feuille de calcul, déterminer le nuage de points associés à l'approximation de la courbe représentative de \text{F} obtenus à l'aide de la méthode d'Euler. On utilisera un pas h = 0{,}1.
2. Tracer la représentation graphique de la fonction x \mapsto 2 \sqrt{x}. Que peut‑on observer ?
On cherche à approcher, en utilisant la méthode d'Euler, la primitive de f \operatorname{sur}[1 \:; 10] vérifiant \mathrm{F}(1)=2.
1. À l'aide d'une feuille de calcul, déterminer le nuage de points associés à l'approximation de la courbe représentative de \text{F} obtenus à l'aide de la méthode d'Euler. On utilisera un pas h = 0{,}1.
2. Tracer la représentation graphique de la fonction x \mapsto 2 \sqrt{x}. Que peut‑on observer ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 102
Tableur
[Représenter.]
Soit f la fonction définie sur \mathrm{I}=[0 \:; 0{,}5] par : f(x)=\frac{1}{1-x^{2}}.
À l'aide de la méthode d'Euler, on veut déterminer de manière approchée la primitive \mathrm{F} de f sur [0 \:; 0{,}5] vérifiant \mathrm{F}(0)=1. On choisit un pas h=0{,}05.
1. En choisissant un pas de 0{,}05, avec combien de points allons‑nous approcher la courbe représentative de la primitive cherchée ?
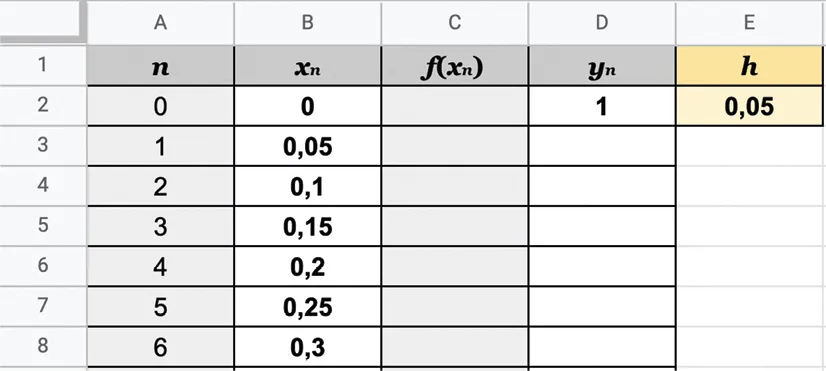
2. a. Quelle formule doit‑on entrer en C2 afin de calculer les images de x_n ?
b. En utilisant l'approximation affine \mathrm{F}(a+h) \approx \mathrm{F}(a)+h \times f(a), donner la formule à entrer en D3 pour compléter par copie la colonne D de la feuille de calcul.
3. Afficher le nuage de points approchant la courbe représentative de la fonction \text{F.}
4. En complément du nuage de points, utiliser le tableur pour faire apparaître la courbe représentative de la fonction g définie par g(x)=\operatorname{argth}(x)+1.
Aide
Sur tableur, la fonction x \mapsto \operatorname{argth}(x) s'utilise avec la commande {\color{purple}\text{ATANH}}.
Quelle conjecture peut‑on émettre ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 103
Tableur
[Représenter.]
Soit f la fonction définie sur \mathrm{I}=[0 \:; 10] par : f(x)=\frac{1}{\sqrt{1+x^{2}}}.
On souhaite déterminer, par la méthode d'Euler, une approximation de la courbe représentative de la primitive \mathrm{F} de f vérifiant \mathrm{F}(0)=0. On choisira dans cet exercice un pas h=0{,}5.
1. En utilisant l'approximation affine \mathrm{F}(a+h) \approx \mathrm{F}(a)+h \times f(a), compléter le tableau ci‑dessous.
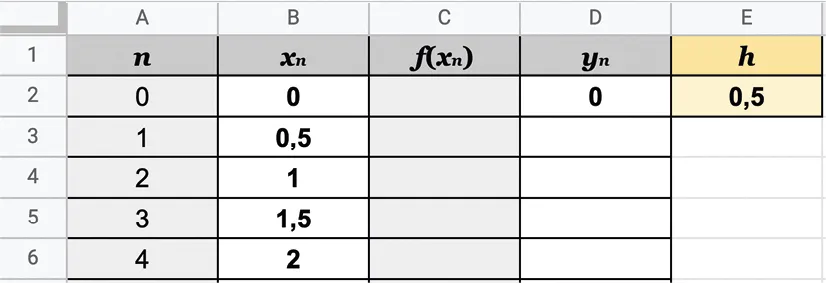
2. Construire le nuage de points approchant la courbe représentative de la fonction \text{F.}
3. Tracer, à l'aide du logiciel utilisé, la courbe représentative de la fonction \operatorname{argsh}(x). Que peut-on constater ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
