Une méthode numérique d'approximation de primitives : la méthode d'Euler

On cherche à trouver sur \text{I} la primitive \text{F} d'une fonction f vérifiant \text{F}(x_0) = y_0.
\text{F} étant une primitive de f, on a, par définition, \mathrm{F}^{\prime}(x)=f(x).
La méthode d'Euler est une méthode numérique qui permet de construire une approximation de la courbe représentative de \text{F} sur un intervalle \text{I.}

Lorsque h est proche de 0 et que a appartient à \text{I,} une approximation de \text{F} en a + h est donnée par l'égalité \mathrm{F}(a+h) \approx \mathrm{F}(a)+h \times \mathrm{F}^{\prime}(a) (voir

chapitre 9

).

• On choisit un pas h > 0 ;
• on pose, pour tout entier naturel n, x_{n+1}=x_{n}+h et y_{n+1}=y_{n}+h \times f\left(x_{n}\right) ;
• on définit les points \mathrm{M}\left(x_{n} ; y_{n}\right) proches de la courbe représentative de \text{F.}

On cherche à construire de manière approchée la primitive \text{F} de la fonction f définie sur [0\:;0{,}5] par f(x)=-\frac{1}{\sqrt{1-x^{2}}} et vérifiant \mathrm{F}(0)=\frac{\pi}{2}.

On va construire un nuage de points permettant d'approcher la représentation graphique de \text{F} avec un pas valant, par exemple, 0{,}05.

L'égalité \mathrm{F}(0)=\frac{\pi}{2} donne x_0 =0 et y_{0}=\frac{\pi}{2}.

Les valeurs successives de x_n s'obtiennent en ajoutant h à chaque fois (ici 0{,}05). Les valeurs successives de y_n s'obtiennent à l'aide de l'approximation y_{n+1} = y_n + h \times f(x_n).

On obtient le tableau ci‑dessous, en inscrivant dans la cellule B2 la valeur de x_0, soit 0, dans la cellule C2 la formule =-1/sqrt(1-B2^2), correspondant à la fonction f, dans la cellule D2 la valeur de y_0, soit \frac{\pi}{2} et en E2 la valeur du pas choisi, ici 0{,}05.


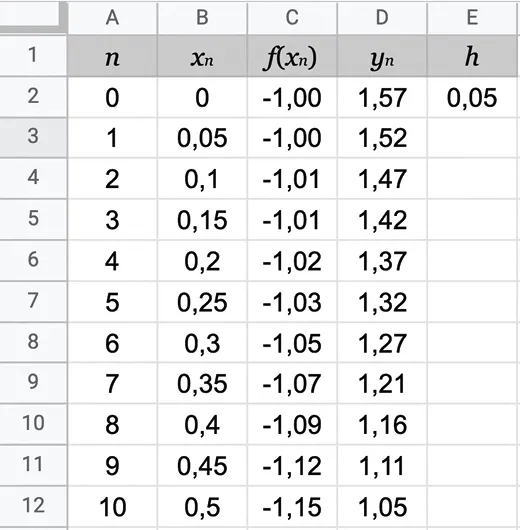
Enfin, on complète la cellule D3 avec l'approximation =D2+$E$2*C2. On étire ensuite toutes ces formules vers le bas.
On obtient le nuage suivant.


La courbe représentée ci‑dessus est celle de la fonction {\color{purple}\bm{\arccos}}, qui correspond à la primitive de f cherchée. On observe que les points obtenus par la méthode d'Euler sont effectivement très proches de la courbe représentative de la fonction {\color{purple}\bm{\arccos}}.