Mathématiques 1re Techno
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Analyse
Ch. 1
Suites
Ch. 2
Fonctions
Ch. 3
Dérivation
Partie 2 : Statistiques et probabilités
Ch. 4
Fréquences conditionnelles et probabilités conditionnelles
Ch. 5
Variables aléatoires
Automatismes
Partie 3 : Géométrie
Ch. 6
Trigonométrie
Ch. 7
Produit scalaire
Ch. 8
Nombres complexes
Partie 4 : Analyse
Ch. 9
Compléments sur la dérivation
Ch. 10
Primitives
Révisions Genially
Chapitre 7
Entraînement 2
Produit scalaire et orthogonalité
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 86
[Raisonner.]
On se place dans un repère orthonormé. Déterminer si les vecteurs \vec{u} et \vec{v} sont orthogonaux.
1. \vec{u}\left(\begin{array}{c} 3 \\ -7 \end{array}\right) et \vec{v}\left(\begin{array}{c} 14 \\ 6 \end{array}\right).
2. \vec{u}\left(\begin{array}{l} \frac{4}{5} \\ \frac{5}{9} \end{array}\right) et \vec{v}\left(\begin{array}{l} -\frac{1}{2} \\ \frac{18}{25} \end{array}\right).
3. \vec{u}\left(\begin{array}{c} -10 \\ 2 \end{array}\right) et \vec{v}\left(\begin{array}{c} 5 \\ -1 \end{array}\right).
1. \vec{u}\left(\begin{array}{c} 3 \\ -7 \end{array}\right) et \vec{v}\left(\begin{array}{c} 14 \\ 6 \end{array}\right).
2. \vec{u}\left(\begin{array}{l} \frac{4}{5} \\ \frac{5}{9} \end{array}\right) et \vec{v}\left(\begin{array}{l} -\frac{1}{2} \\ \frac{18}{25} \end{array}\right).
3. \vec{u}\left(\begin{array}{c} -10 \\ 2 \end{array}\right) et \vec{v}\left(\begin{array}{c} 5 \\ -1 \end{array}\right).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Consigne
Pour les et
Soient \mathrm{A}, \mathrm{B}, \mathrm{C} et \text{D} quatre points du plan muni d'un repère orthonormé. Étudier l'orthogonalité des droites (\mathrm{AB}) et \text {(CD)}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 87
[Raisonner.]
1.
\mathrm{A}(-7 \: ; 4), \mathrm{B}(-1 \: ; 6), \mathrm{C}(-10 \: ; 3) et \mathrm{D}(-8 \: ;-3).
2. \mathrm{A}(2 \: ; 4), \mathrm{B}(-1 \: ; 3), \mathrm{C}(2 \: ; 1) et \mathrm{D}(-11 \: ; 5).
3. \mathrm{A}(4 \: ;-1), \mathrm{B}(1 \: ; 4), \mathrm{C}(7 ;-6) et \mathrm{D}(14 \: ;-2).
2. \mathrm{A}(2 \: ; 4), \mathrm{B}(-1 \: ; 3), \mathrm{C}(2 \: ; 1) et \mathrm{D}(-11 \: ; 5).
3. \mathrm{A}(4 \: ;-1), \mathrm{B}(1 \: ; 4), \mathrm{C}(7 ;-6) et \mathrm{D}(14 \: ;-2).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 88
[Raisonner.]
1.
\mathrm{A}\left(\frac{1}{2} \: ;-\frac{3}{2}\right), \mathrm{B}\left(\frac{2}{5} \: ; \frac{3}{5}\right), \mathrm{C}(1 \: ;-12) et \mathrm{D}\left(15 \: ;-\frac{34}{3}\right).
2. \mathrm{A}(2 \sqrt{2} \: ;-2 \sqrt{2}), \mathrm{B}(-2 \: ; 2), \mathrm{C}(\sqrt{3} \: ;-\sqrt{3}) et \mathrm{D}(3 \sqrt{3} \: ; \sqrt{3}).
3. \mathrm{A}(1-\sqrt{3} \: ; 2), \mathrm{B}(\sqrt{3} \: ; 1), \mathrm{C}(\sqrt{3} \: ;-5) et \mathrm{D}(3 \sqrt{3}+1 \: ; 6).
2. \mathrm{A}(2 \sqrt{2} \: ;-2 \sqrt{2}), \mathrm{B}(-2 \: ; 2), \mathrm{C}(\sqrt{3} \: ;-\sqrt{3}) et \mathrm{D}(3 \sqrt{3} \: ; \sqrt{3}).
3. \mathrm{A}(1-\sqrt{3} \: ; 2), \mathrm{B}(\sqrt{3} \: ; 1), \mathrm{C}(\sqrt{3} \: ;-5) et \mathrm{D}(3 \sqrt{3}+1 \: ; 6).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 89
[Chercher.]
Soient \mathrm{A}(5 \: ;-2), \mathrm{B}(x \: ;-1), \mathrm{C}(-3 \: ; 4) et \mathrm{D}(7 \: ;-4) quatre points du plan muni d'un repère orthonormé.
Dans chaque cas, déterminer le réel x tel que les vecteurs donnés soient orthogonaux.
1. \overrightarrow{\mathrm{AB}} et \overrightarrow{\mathrm{CD}}
2. \overrightarrow{\mathrm{AB}} et \overrightarrow{\mathrm{AC}}
3. \overrightarrow{\mathrm{AC}} et \overrightarrow{\mathrm{BD}}
4. \overrightarrow{\mathrm{BC}} et \overrightarrow{\mathrm{AD}}
Dans chaque cas, déterminer le réel x tel que les vecteurs donnés soient orthogonaux.
1. \overrightarrow{\mathrm{AB}} et \overrightarrow{\mathrm{CD}}
2. \overrightarrow{\mathrm{AB}} et \overrightarrow{\mathrm{AC}}
3. \overrightarrow{\mathrm{AC}} et \overrightarrow{\mathrm{BD}}
4. \overrightarrow{\mathrm{BC}} et \overrightarrow{\mathrm{AD}}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 90
Vrai / Faux
[Raisonner.]
Soit \text{ABCD} un carré de centre \text{S} tel que \mathrm{AB}=8. On note \mathrm{E}, \mathrm{F}, \mathrm{G} et \text{H} les milieux respectifs des segments [\mathrm{AB}],[\mathrm{BC}],[\mathrm{CD}] et [\mathrm{AD}].

Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse en justifiant la réponse.
1. \overrightarrow{\mathrm{AE}} \cdot \overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{AE}} \cdot \overrightarrow{\mathrm{AB}}
2. \overrightarrow{\mathrm{EH}} \cdot \overrightarrow{\mathrm{FG}}=0
3. \overrightarrow{\mathrm{AB}} \cdot \overrightarrow{\mathrm{SC}}=\overrightarrow{\mathrm{AB}} \cdot \overrightarrow{\mathrm{EB}}
4. \overrightarrow{\mathrm{DS}} \cdot \overrightarrow{\mathrm{EB}}=\overrightarrow{\mathrm{AE}} \cdot \overrightarrow{\mathrm{AE}}
5. \overrightarrow{\mathrm{GF}} \cdot \overrightarrow{\mathrm{GE}}=\overrightarrow{\mathrm{SF}} \cdot \overrightarrow{\mathrm{SE}}
6. \overrightarrow{\mathrm{BH}} \cdot \overrightarrow{\mathrm{FD}}=\overrightarrow{\mathrm{ES}} \cdot \overrightarrow{\mathrm{FF}}

Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse en justifiant la réponse.
1. \overrightarrow{\mathrm{AE}} \cdot \overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{AE}} \cdot \overrightarrow{\mathrm{AB}}
2. \overrightarrow{\mathrm{EH}} \cdot \overrightarrow{\mathrm{FG}}=0
3. \overrightarrow{\mathrm{AB}} \cdot \overrightarrow{\mathrm{SC}}=\overrightarrow{\mathrm{AB}} \cdot \overrightarrow{\mathrm{EB}}
4. \overrightarrow{\mathrm{DS}} \cdot \overrightarrow{\mathrm{EB}}=\overrightarrow{\mathrm{AE}} \cdot \overrightarrow{\mathrm{AE}}
5. \overrightarrow{\mathrm{GF}} \cdot \overrightarrow{\mathrm{GE}}=\overrightarrow{\mathrm{SF}} \cdot \overrightarrow{\mathrm{SE}}
6. \overrightarrow{\mathrm{BH}} \cdot \overrightarrow{\mathrm{FD}}=\overrightarrow{\mathrm{ES}} \cdot \overrightarrow{\mathrm{FF}}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 91
[Raisonner.]
Soit \text{ABCD} un rectangle tel que \mathrm{AD}=6 et \mathrm{AB}=2 \times \mathrm{AD}.
On définit les points \text{E} et \text{F} par les relations vectorielles suivantes : {\overrightarrow{\mathrm{AE}}=\frac{5}{3} \overrightarrow{\mathrm{AD}}} et {\overrightarrow{\mathrm{AF}}=\frac{1}{3} \overrightarrow{\mathrm{AC}}.}
Démontrer que les droites \text{(AF)} et \text{(EF)} sont perpendiculaires.
On définit les points \text{E} et \text{F} par les relations vectorielles suivantes : {\overrightarrow{\mathrm{AE}}=\frac{5}{3} \overrightarrow{\mathrm{AD}}} et {\overrightarrow{\mathrm{AF}}=\frac{1}{3} \overrightarrow{\mathrm{AC}}.}
Démontrer que les droites \text{(AF)} et \text{(EF)} sont perpendiculaires.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 92
[Raisonner.]
Soit \text{ABCD} un rectangle tel que \mathrm{AB}=6 et \mathrm{AD}=2.

Calculer \overrightarrow{\mathrm{AB}} \cdot \overrightarrow{\mathrm{AC}}.

Calculer \overrightarrow{\mathrm{AB}} \cdot \overrightarrow{\mathrm{AC}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
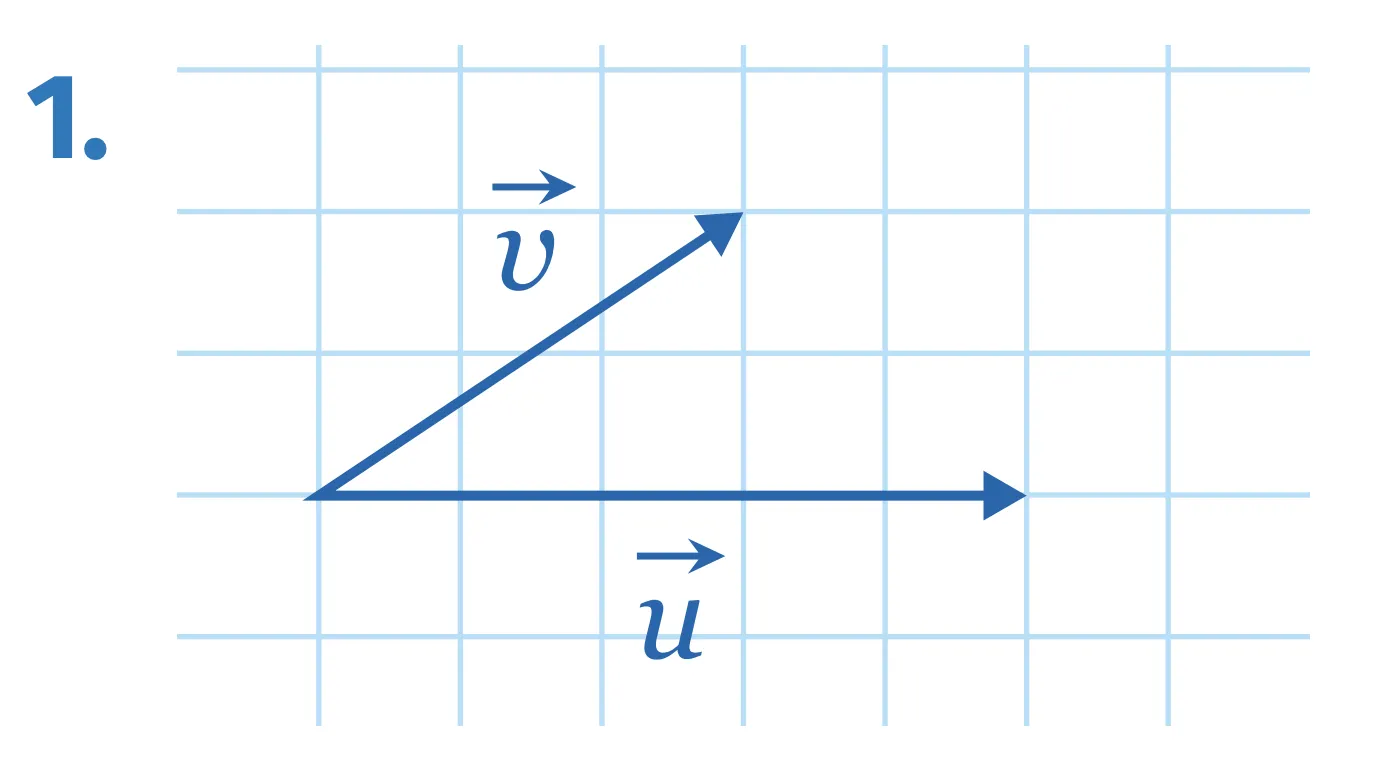
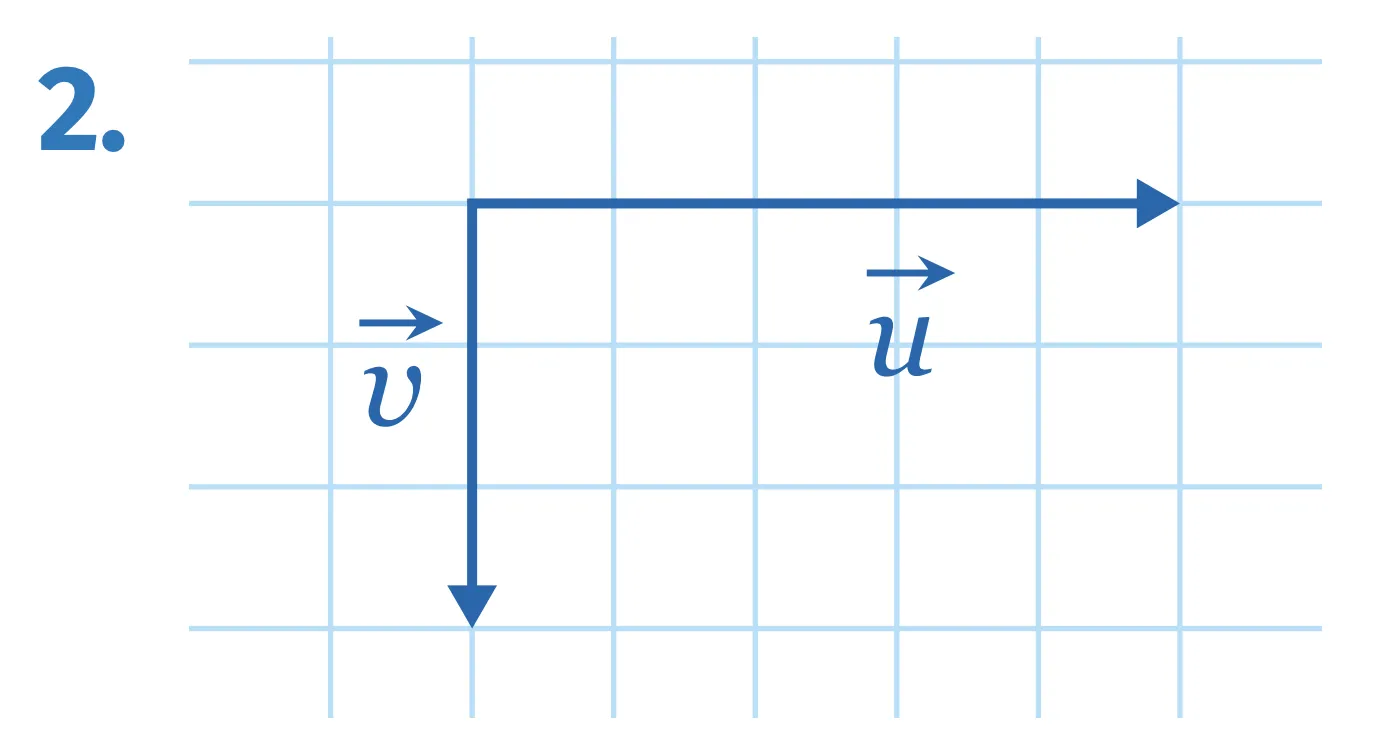
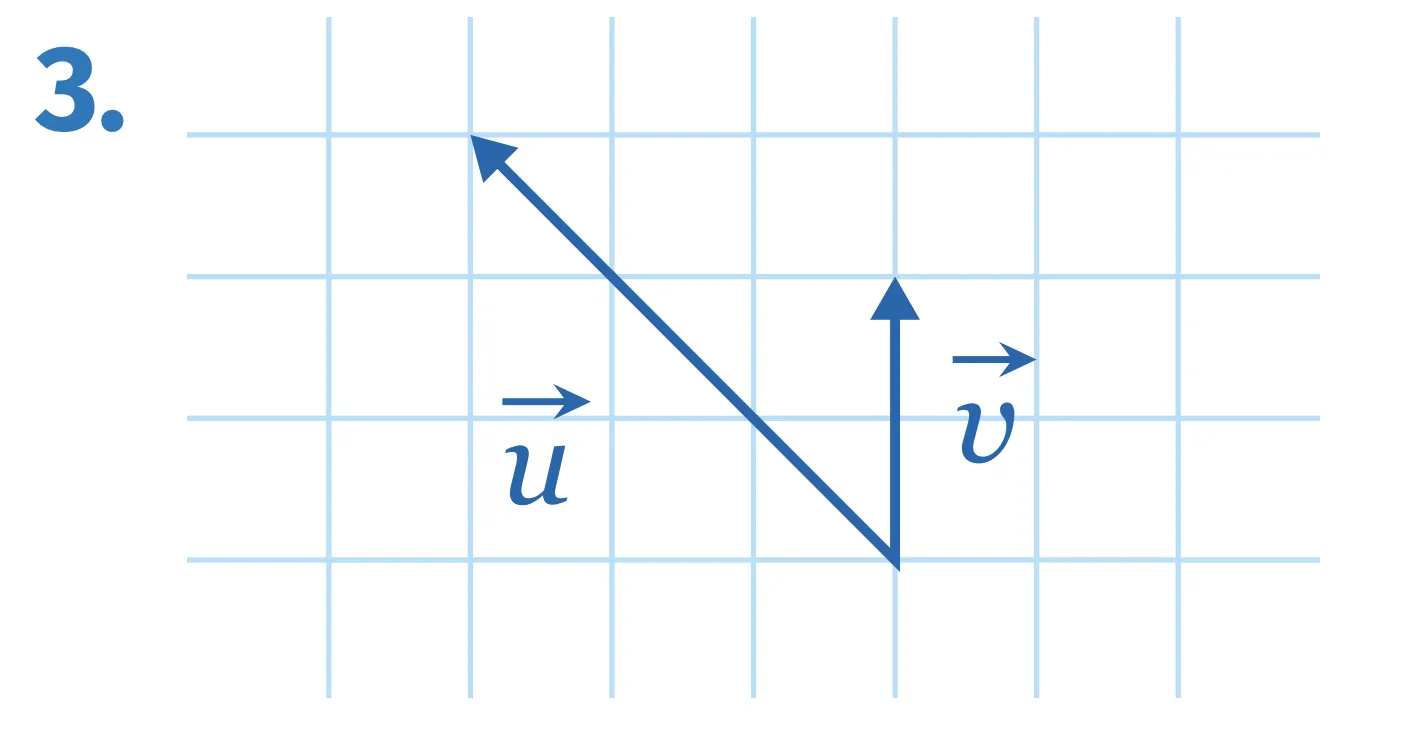
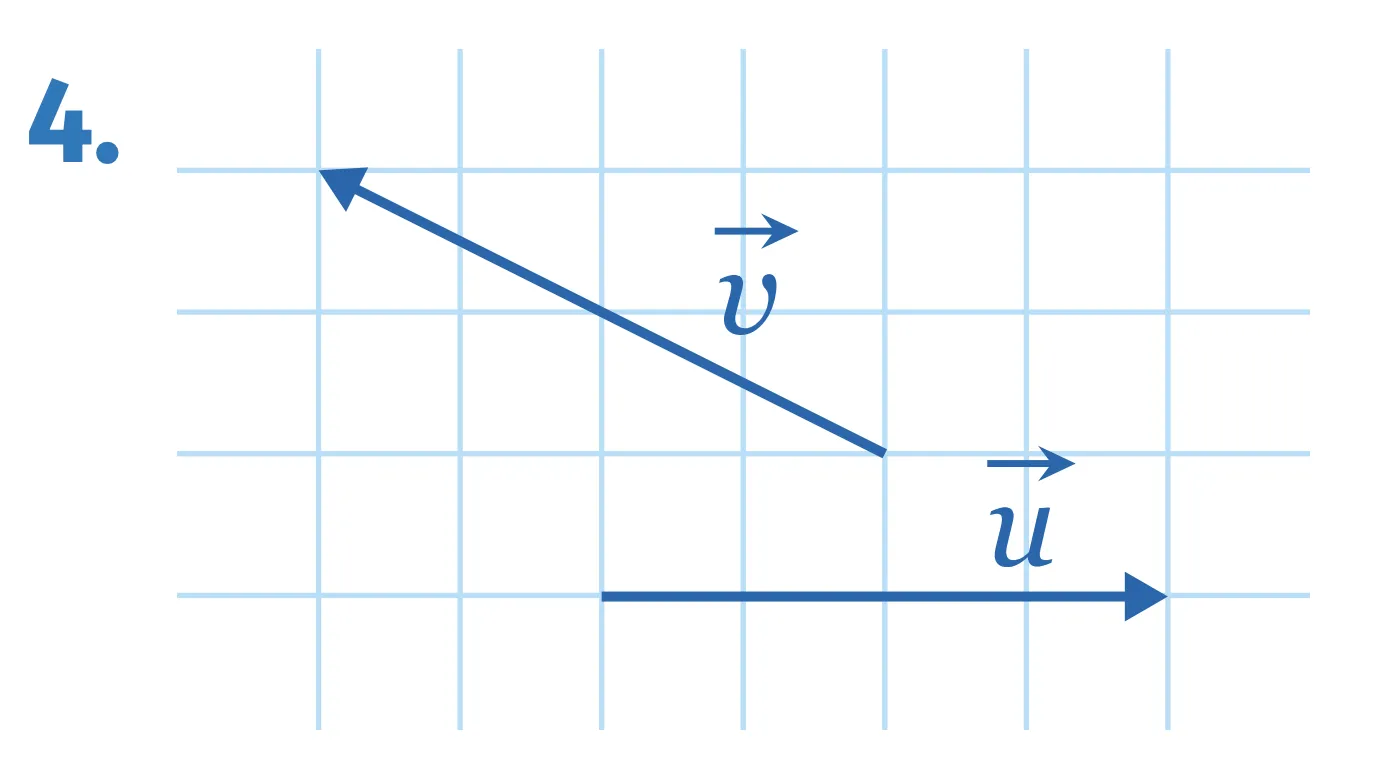
Exercice 93
[Représenter.]
Dans les figures ci‑dessous, chaque carreau correspond à un carré de côté 1. Dans chaque cas, calculer \vec{u} \cdot \vec{v}.












Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 94
GeoGebra
[Modéliser.]
Dans un repère orthonormé, on considère les points \mathrm{A}(2 \: ; a+1), \mathrm{B}(a \: ; 3 a-2), \mathrm{C}(a+1 \: ; 2) et \mathrm{D}(-a-4 \: ; 3 a-3), où a désigne un nombre réel.
1. Ouvrir le logiciel GeoGebra.
a. Définir un curseur a variant de -5 à 5 avec un incrément de 0{,}5.
b. Définir ensuite les points \mathrm{A}, \mathrm{B}, \mathrm{C} et \text{D}.
c. En faisant varier le curseur a, déterminer la valeur de a telle que les droites \text{(AB)} et \text{(CD)} soient perpendiculaires.
2. a. Exprimer les coordonnées des vecteurs \overrightarrow{\mathrm{AB}} et \overrightarrow{\mathrm{CD}} en fonction de a.
b. Démontrer la conjecture émise à la question 1. c.
1. Ouvrir le logiciel GeoGebra.
a. Définir un curseur a variant de -5 à 5 avec un incrément de 0{,}5.
b. Définir ensuite les points \mathrm{A}, \mathrm{B}, \mathrm{C} et \text{D}.
c. En faisant varier le curseur a, déterminer la valeur de a telle que les droites \text{(AB)} et \text{(CD)} soient perpendiculaires.
2. a. Exprimer les coordonnées des vecteurs \overrightarrow{\mathrm{AB}} et \overrightarrow{\mathrm{CD}} en fonction de a.
b. Démontrer la conjecture émise à la question 1. c.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 95
[Représenter.]
Dans un repère orthonormé (\mathrm{O} \: ; \vec{i}, \vec{j}) du plan, on considère un vecteur \vec{u} de norme 5 tel qu'une mesure de l'angle entre les vecteurs \vec{i} et \vec{u} soit \frac{\pi}{4}.

Déterminer, en fonction de \vec{i}, la projection orthogonale de \vec{u} sur l'axe des abscisses.

Déterminer, en fonction de \vec{i}, la projection orthogonale de \vec{u} sur l'axe des abscisses.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 96
Exercice inversé
Soit \text{ABCD} un trapèze rectangle.

Déterminer tous les produits scalaires égaux à 4.

Déterminer tous les produits scalaires égaux à 4.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 97
Exercice inversé
Dans un repère orthonormé du plan, on considère \mathrm{A}(1 \: ; 2) et \mathrm{B}(-3 \: ; 5).
1. Proposer des coordonnées de deux points \text{C} et \text{D} tels que \text{(AB)} et \text{(CD)} soient perpendiculaires.
2. Proposer des coordonnées de deux points \text{E} et \text{F} tels que \text{(AE)} et \text{(BF)} soient perpendiculaires.
1. Proposer des coordonnées de deux points \text{C} et \text{D} tels que \text{(AB)} et \text{(CD)} soient perpendiculaires.
2. Proposer des coordonnées de deux points \text{E} et \text{F} tels que \text{(AE)} et \text{(BF)} soient perpendiculaires.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
