Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Thème 1 : Une longue histoire de la matière
Ch. 1
Les éléments chimiques
Ch. 2
Des édifices ordonnés : les cristaux
Ch. 3
Une structure complexe : la cellule
Thème 2 : Le Soleil, notre source d'énergie
Ch. 4
Le rayonnement solaire
Ch. 5
Le bilan radiatif terrestre
Ch. 6
Énergie solaire et photosynthèse
Ch. 7
Le bilan thermique du corps humain
Thème 3 : La Terre, un astre singulier
Ch. 8
La forme de la Terre
Ch. 9
L'histoire de l’âge de la Terre
Ch. 10
La Terre dans l’Univers
Thème 4 : Son et musique, porteurs d'information
Ch. 11
Le son, phénomène vibratoire
Ch. 12
Musique et nombres
Ch. 13
Le son, une information à coder
Ch. 14
Entendre la musique
Projet Experimental et Numérique
Livret Maths
Annexes
Chapitre 2
Exercices
L'atelier des apprentis
10 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Les silicates d'alumine, témoins d'une histoire
✔ Relier la structure d'une roche à des conditions physiques
Les silicates d'alumine permettent de reconstruire une histoire géologique. On étudie un gneiss à sillimanite (roche métamorphique) échantillonné en surface.
Retrouvez le parcours subi par la roche, expliquant la présence de sillimanite et sa localisation en surface.
Les silicates d'alumine permettent de reconstruire une histoire géologique. On étudie un gneiss à sillimanite (roche métamorphique) échantillonné en surface.
Question
Retrouvez le parcours subi par la roche, expliquant la présence de sillimanite et sa localisation en surface.
Doc.
Diagramme P/T et domaines de stabilité de trois silicates d'alumine
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Les deux structures cristallines courantes du fer
✔ Calculer la masse volumique d'un cristal
Le fer présente plusieurs structures cristallines dites allotropiques. Le fer \alpha (alpha) possède une structure type cubique centrée tandis que le fer \gamma (gamma) possède une structure type cubique à faces centrées de paramètre a = 0\text{,}356 nm.
Masse d'un atome de fer : m_{\text{Fe}} = 9\text{,}27 \times 10^{-26} kg
1. Représentez la maille de la structure du fer \gamma en perspective cavalière et déduisez-en le rayon atomique du fer dans ce cas.
Le fer présente plusieurs structures cristallines dites allotropiques. Le fer \alpha (alpha) possède une structure type cubique centrée tandis que le fer \gamma (gamma) possède une structure type cubique à faces centrées de paramètre a = 0\text{,}356 nm.
Données
Masse d'un atome de fer : m_{\text{Fe}} = 9\text{,}27 \times 10^{-26} kg
1. Représentez la maille de la structure du fer \gamma en perspective cavalière et déduisez-en le rayon atomique du fer dans ce cas.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
2. Calculez la masse volumique du fer dans cette structure.
Doc.
Diagramme de phase des variétés allotropiques du ferLe zoom est accessible dans la version Premium.
Instant maths
Retrouvez des rappels de cours et des exercices d'application sur la perspective cavalière .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3CaCO3 dans tous ses états ! Une affaire de système cristallin
✔ Confronter des données nouvelles à ses connaissances
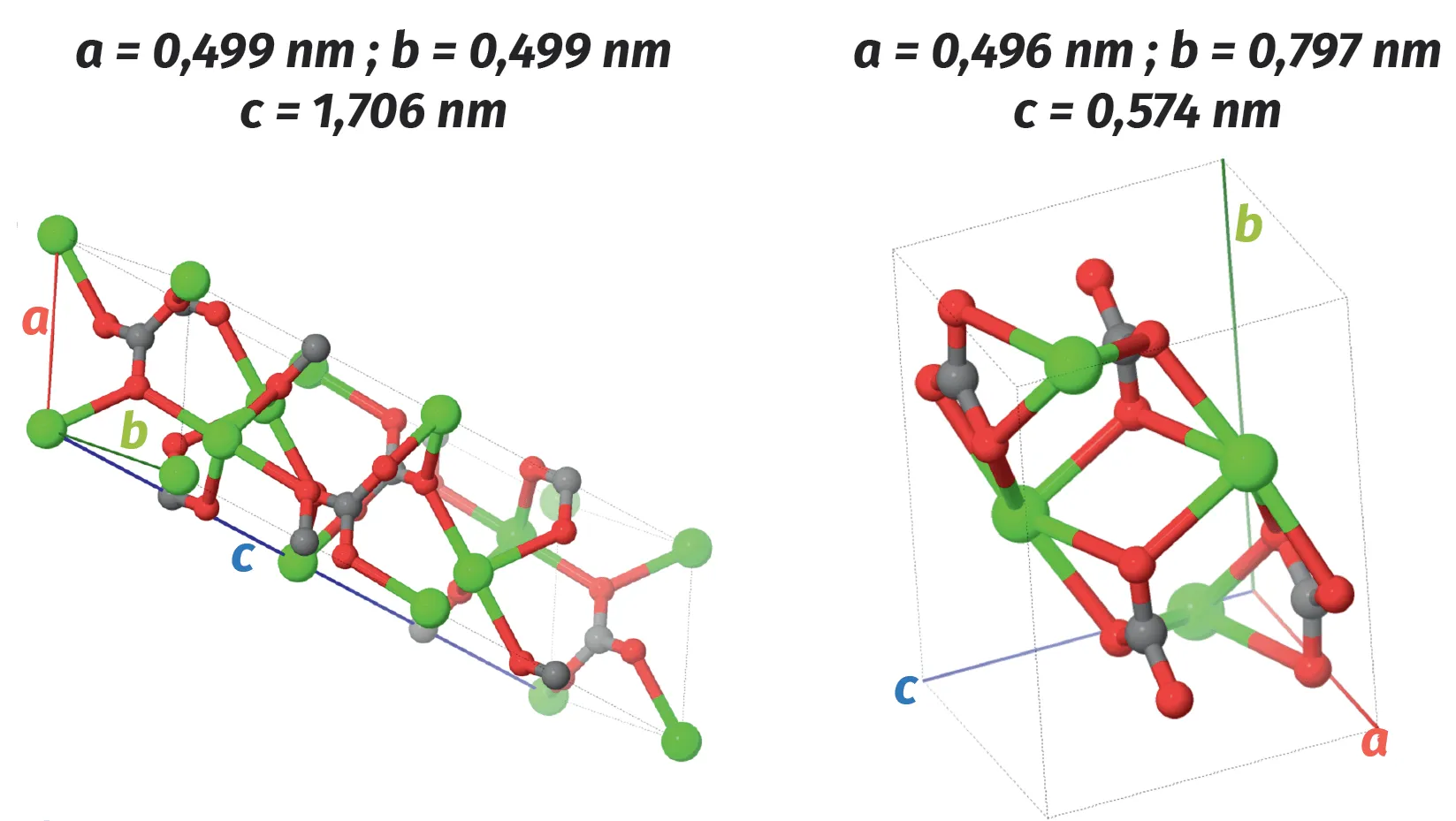
Le carbonate de calcium a pour formule chimique CaCO3. Les géologues le connaissent sous différentes formes de cristaux dont les plus connus sont la calcite et l'aragonite.
1. D'après les modèles moléculaires, ces minéraux cristallisent-ils dans les structures cubiques ou CFC ? Justifiez à l'aide des paramètres de maille.
2. Grâce à vos connaissances complétées par une recherche sur Internet, trouvez des structures d'organismes vivants constituées de ces cristaux.
Le carbonate de calcium a pour formule chimique CaCO3. Les géologues le connaissent sous différentes formes de cristaux dont les plus connus sont la calcite et l'aragonite.
1. D'après les modèles moléculaires, ces minéraux cristallisent-ils dans les structures cubiques ou CFC ? Justifiez à l'aide des paramètres de maille.
2. Grâce à vos connaissances complétées par une recherche sur Internet, trouvez des structures d'organismes vivants constituées de ces cristaux.
Doc.
Modèles cristallins de la calcite et de l'aragonite
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ALa carboglace
✔ Déterminer les paramètres géométriques d'une maille
La carboglace, de formule chimique CO2, correspond à la forme solide du dioxyde de carbone. Elle cristallise sous la forme d'un réseau cubique à faces centrées.
Masse d'une molécule de CO2 : m = 7\text{,}31 \times 10^{-26} kg
La masse volumique de la carboglace vaut
⍴ =1,56×103 kg ·m^{-3}
1. En supposant que la carboglace cristallise selon une structure CFC, établir le nombre de molécules par maille.
2. En déduire le paramètre ɑ de la maille.
3. En utilisant le théorème de Pythagore pour déterminer la diagonale d'une face de la maille en fonction de ɑ, en déduire la distance D entre deux atomes de carbone de deux molécules voisines selon cette diagonale.
La carboglace, de formule chimique CO2, correspond à la forme solide du dioxyde de carbone. Elle cristallise sous la forme d'un réseau cubique à faces centrées.
Données
1. En supposant que la carboglace cristallise selon une structure CFC, établir le nombre de molécules par maille.
2. En déduire le paramètre ɑ de la maille.
3. En utilisant le théorème de Pythagore pour déterminer la diagonale d'une face de la maille en fonction de ɑ, en déduire la distance D entre deux atomes de carbone de deux molécules voisines selon cette diagonale.
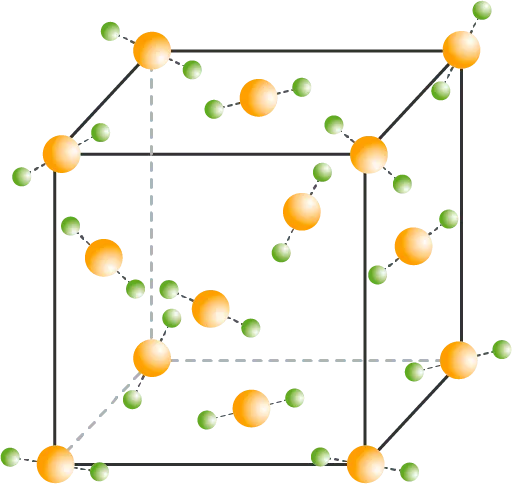
Doc.
Carboglace et structure cristalline
Le zoom est accessible dans la version Premium.
Le zoom est accessible dans la version Premium.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah