Physique-Chimie 1re Spécialité
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
1. Constitution et transformations de la matière
Ch. 1
Composition chimique d'un système
Ch. 2
Composition chimique des solutions
Ch. 3
Évolution d'un système chimique
Ch. 4
Réactions d'oxydoréduction
Ch. 5
Détermination d'une quantité de matière par titrage
Livret Bac : Thème 1
Ch. 6
De la structure à la polarité d'une entité
Ch. 7
Interpréter les propriétés d’une espèce chimique
Ch. 8
Structure des entités organiques
Ch. 9
Synthèse d'espèces chimiques organiques
Ch. 10
Conversions d'énergie au cours d'une combustion
Livret Bac : Thème 1 bis
2. Mouvement et interactions
Ch. 11
Modélisation d'interactions fondamentales
Ch. 12
Description d'un fluide au repos
Ch. 13
Mouvement d'un système
Livret Bac : Thème 2
3. L'énergie, conversions et transferts
Ch. 14
Études énergétiques en électricité
Ch. 15
Études énergétiques en mécanique
Livret Bac : Thème 3
4. Ondes et signaux
Ch. 16
Ondes mécaniques
Ch. 17
Images et couleurs
Ch. 18
Modèles ondulatoire et particulaire de la lumière
Livret Bac : Thème 4
Méthode
Fiches méthode
Fiche méthode compétences
Annexes
Chapitre 2
Cours
Composition chimique des solutions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Espèce colorée en solution
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
AConcentration d'une espèce dissoute
La concentration d'un soluté en solution s'exprime en utilisant :
Ces deux concentrations sont liées par la relation :
\gamma=c \cdot M \quad{M} étant la masse molaire du soluté en g·mol-1.
Dans le cas d'un soluté ionique, les espèces présentes en solution après dissolution sont différentes du soluté initialement dissous.
[\mathrm{X}]=\dfrac{n_{\mathrm{X}}}{V_{\text {solution }}} exprime la concentration en quantité de matière de l'espèce \text{X} en mol·L-1, avec n_{X} en mol et V_\text {solution } en L.
- soit la concentration en masse \gamma :
\gamma=\dfrac{m_{\text { soluté }}}{V_{\text {solution }}} avec \gamma en g·L-1 ; la masse m_\text{ soluté} en g ; et le volume V_\text {solution} de la solution en L. - soit la concentration c en quantité de matière :
c=\dfrac{n_{\text { soluté }}}{V_{\text{solution }}} avec c en mol·L-1 ; la quantité de matière n_\text { soluté } en mol ; le volume V_\text{solution } de la solution en L.
Ces deux concentrations sont liées par la relation :
\gamma=c \cdot M \quad{M} étant la masse molaire du soluté en g·mol-1.
Dans le cas d'un soluté ionique, les espèces présentes en solution après dissolution sont différentes du soluté initialement dissous.
[\mathrm{X}]=\dfrac{n_{\mathrm{X}}}{V_{\text {solution }}} exprime la concentration en quantité de matière de l'espèce \text{X} en mol·L-1, avec n_{X} en mol et V_\text {solution } en L.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La concentration c informe sur la quantité de soluté
apportée par unité de volume et la notation [\text{X}] renseigne la concentration de l'espèce chimique \text{X} effectivement présente dans la solution.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
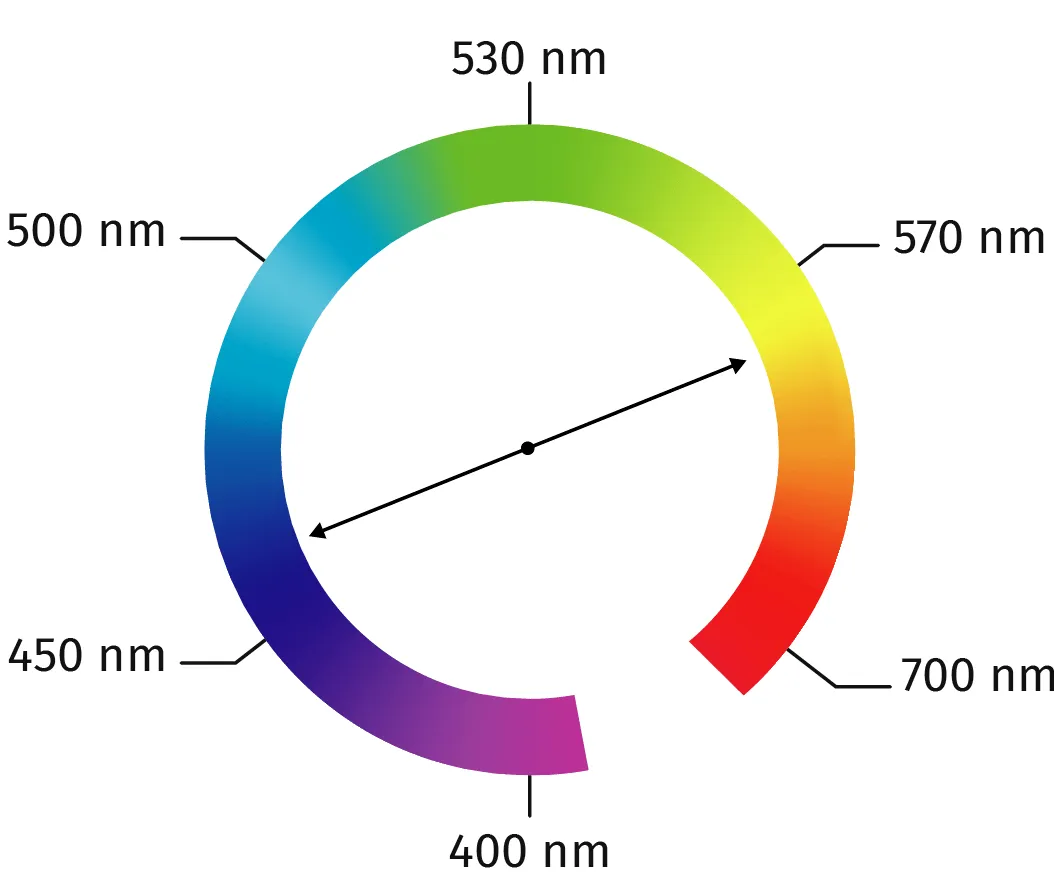
Doc. 1 Cercle chromatique simplifié

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
B Couleur d'une solution
Lorsqu'une solution est traversée par de la lumière blanche. Certaines
radiations sont absorbées et d'autres sont transmises. La couleur perçue d'une solution est complémentaire des radiations absorbées qui traversent la solution. Des couleurs complémentaires
sont diamètralement opposées sur le cercle chromatique (doc. 1).Plus la concentration d'une espèce chimique colorée en solution est élévée, plus les radiations sont absorbées, et plus la solution est foncée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
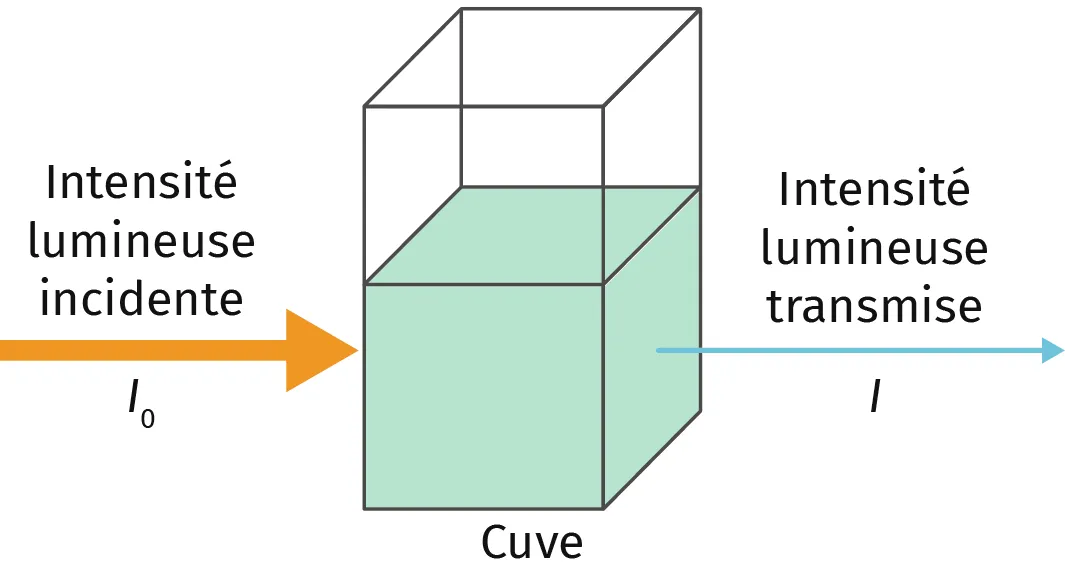
Doc. 2 Absorbance d'une solution

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
C Absorbance
Pour une longueur d'onde donnée, l'absorbance A quantifie la proportion des radiations incidentes d'intensité I_{0} absorbées en mesurant l'intensité des radiations non absorbées I (doc. 2). Pour une espèce chimique, la courbe A = f(\lambda) est appelée spectre d'absorption. Elle permet de déterminer la longueur d'onde, notée \lambda_{\text{max}}, de l'absorbance maximale, notée A_{\text{max}} et correspondant à la couleur complémentaire de la solution (doc. 3).Un spectrophotomètre permet d'effectuer des mesures d'absorbance sur une gamme de longueurs d'onde qui s'étend sur les ultraviolets proches (200 nm à 400 nm) et le domaine visible (400 nm à 800 nm).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 3 Le bleu de méthylène

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application
On dissout une masse m = 0,15 g de chlorure de cobalt de formule \text{Co}\text{Cl}_{2} dans un volume V_{sol} de 50,0 mL d'eau. L'équation de dissolution est : \text{Co}\text{Cl}_{2}(s) → \text{Co}^{2+} (aq) + 2\:\text{Cl}^{-} (aq).
1. Calculer la concentration en masse puis en quantité de matière de soluté dissous.
2. Calculer la concentration d'ions cobalt (II) et d'ions chlorure dissous en solution.
1. \gamma=\dfrac{m}{V}=\dfrac{0\text{,}15}{50\text{,}0 \times 10^{-3}}=3\text{,}0 g·L-1.
Conversion : c=\dfrac{\gamma}{M\left(\mathrm{CoCl}_{2}\right)}=\dfrac{3\text{,}0}{58\text{,}9+2 \times 35\text{,}5}=2\text{,}3 \times 10^{-2} mol·L-1.
2. D'après l'équation de dissolution, 1 mole de chlorure de cobalt produit 1 mole d'ions cobalt (II) et 2 moles d'ions chlorure. Ainsi :
[\text{Co}^{2+}(aq)] =c=2\text{,}3 \times 10^{-2} mol·L-1 et
[\text{Cl}^{-}(aq)] =2 c=4\text{,}6 \times 10^{-2} mol·L-1.
1. Calculer la concentration en masse puis en quantité de matière de soluté dissous.
2. Calculer la concentration d'ions cobalt (II) et d'ions chlorure dissous en solution.
Corrigé
1. \gamma=\dfrac{m}{V}=\dfrac{0\text{,}15}{50\text{,}0 \times 10^{-3}}=3\text{,}0 g·L-1.
Conversion : c=\dfrac{\gamma}{M\left(\mathrm{CoCl}_{2}\right)}=\dfrac{3\text{,}0}{58\text{,}9+2 \times 35\text{,}5}=2\text{,}3 \times 10^{-2} mol·L-1.
2. D'après l'équation de dissolution, 1 mole de chlorure de cobalt produit 1 mole d'ions cobalt (II) et 2 moles d'ions chlorure. Ainsi :
[\text{Co}^{2+}(aq)] =c=2\text{,}3 \times 10^{-2} mol·L-1 et
[\text{Cl}^{-}(aq)] =2 c=4\text{,}6 \times 10^{-2} mol·L-1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 4 Solution de chlorure de cobalt


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Masses molaires en g·mol-1 :
M(\text{Cl})= 35\text{,}5 ;
M(\text{Co})= 58\text{,}9.
M(\text{Cl})= 35\text{,}5 ;
M(\text{Co})= 58\text{,}9.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Dosage spectrophotométrique par étalonnage
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ALoi de Beer-Lambert
Pour une longueur d'onde \lambda donnée, l'absorbance A_{\lambda} d'une espèce chimique en solution diluée est proportionnelle à la concentration c en quantité de matière de cette espèce chimique, à l'épaisseur l de solution traversée et à \epsilon_{\lambda}, le coefficient d'extinction molaire (qui dépend de la nature de l'espèce chimique) : c'est la loi de Beer-Lambert.
Pour des conditions expérimentales données (\lambda, \epsilon_{\lambda} et l fixés) :
avec \text{k} le coefficient de proportionnalité en L·mol-1.
A_{\lambda}=\varepsilon_{\lambda} \cdot l \cdot c
avec A_\lambda sans unité, \epsilon_{\lambda} en L·mol-1·cm-1, l en cm et c en mol·L-1.Pour des conditions expérimentales données (\lambda, \epsilon_{\lambda} et l fixés) :
A_{\lambda}=\text{k} \cdot c
avec \text{k} le coefficient de proportionnalité en L·mol-1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Dans le cas de plusieurs espèces chimiques colorées
en solution, l'absorbance est additive :
A=A(1)+A(2)+\ldots+A(n).
A=A(1)+A(2)+\ldots+A(n).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 5 Courbe d'étalonnage

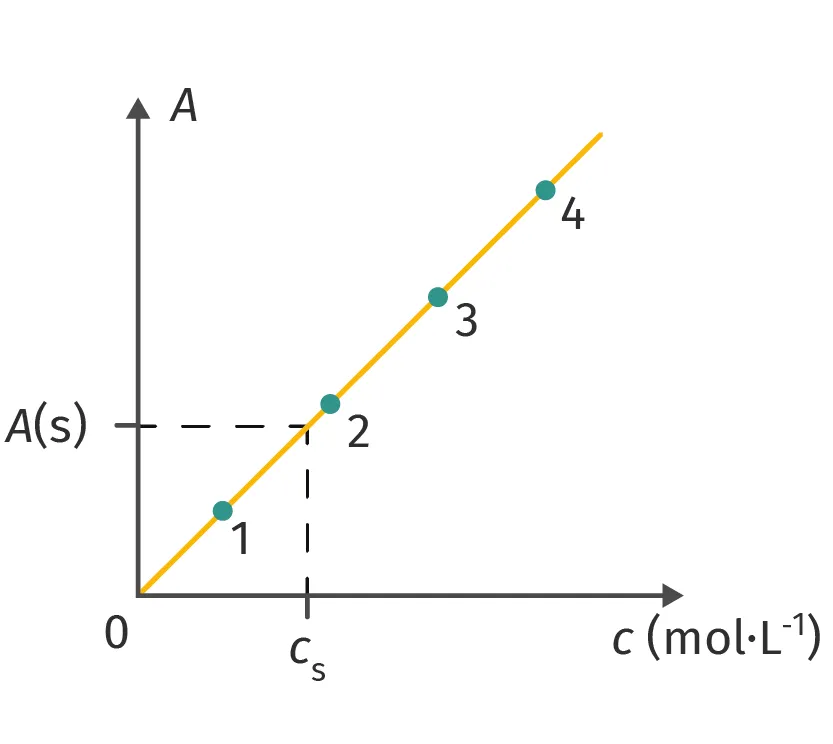
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BDosage spectrophotométrique
par étalonnage
Étapes d'un dosage spectrophotométrique par étalonnage :
1. Déterminer la longueur d'onde \lambda_{\text{max}} pour laquelle le spectre d'absorption de l'espèce chimique présente une absorbance maximale.
2. Pour la longueur d'onde \lambda_{\text{max}}, mesurer l'absorbance des solutions étalons et réaliser la droite d'étalonnage représentant la loi de Beer-Lambert, A_{\lambda}=k \cdot c.
3. Mesurer l'absorbance de la solution à doser et déterminer sa concentration en exploitant la droite d'étalonnage (doc. 5).
1. Déterminer la longueur d'onde \lambda_{\text{max}} pour laquelle le spectre d'absorption de l'espèce chimique présente une absorbance maximale.
2. Pour la longueur d'onde \lambda_{\text{max}}, mesurer l'absorbance des solutions étalons et réaliser la droite d'étalonnage représentant la loi de Beer-Lambert, A_{\lambda}=k \cdot c.
3. Mesurer l'absorbance de la solution à doser et déterminer sa concentration en exploitant la droite d'étalonnage (doc. 5).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une mesure d'absorbance peut être réalisée à n'importe quelle valeur de longueur d'onde. Régler le spectrophotomètre sur la valeur \lambda_{\text{max}} permet de comparer des valeurs plus grandes et minimiser ainsi les incertitudes.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
