Chapitre 2
Bilan
Composition chimique des solutions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Principales notions
La concentration d'une espèce chimique en solution peut s'exprimer de deux façons :
c=\dfrac{n_{\text { soluté }}}{V_{\text {solution }}} (en mol·L-1) ou \gamma=\dfrac{m_{\text { soluté }}}{V_{\text {solution }}} (en g·L-1).
Elles sont liées par la relation : \gamma=c \cdot M.
Avec m_\text{ soluté} en g, n_{\text { soluté }} en mol, V_{\text {solution }} en L et M en g·mol-1.
c=\dfrac{n_{\text { soluté }}}{V_{\text {solution }}} (en mol·L-1) ou \gamma=\dfrac{m_{\text { soluté }}}{V_{\text {solution }}} (en g·L-1).
Elles sont liées par la relation : \gamma=c \cdot M.
Avec m_\text{ soluté} en g, n_{\text { soluté }} en mol, V_{\text {solution }} en L et M en g·mol-1.
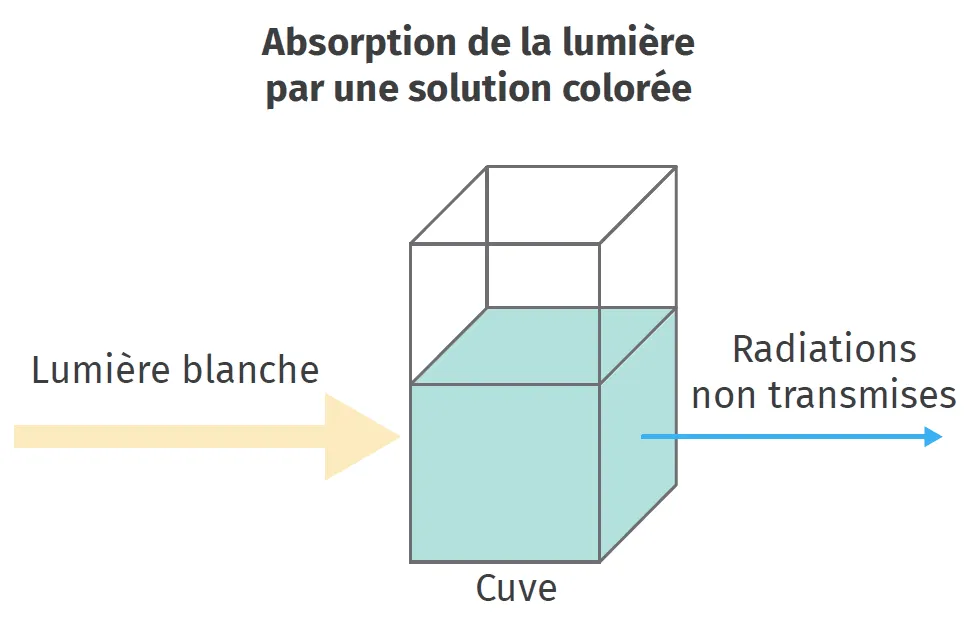
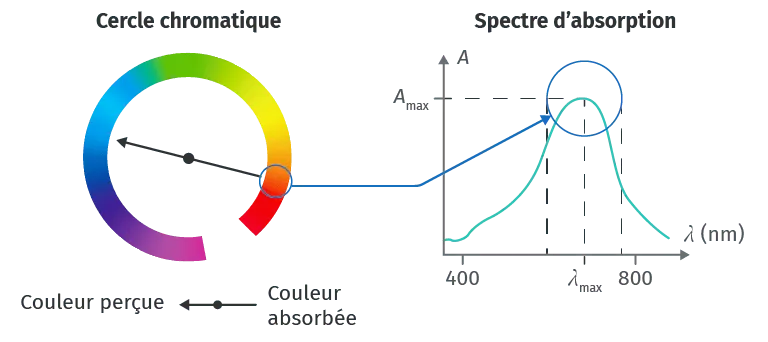
Une espèce chimique peut être caractérisée par son spectre d'absorption qui représente l'évolution de l'absorbance en fonction des longueurs d'onde des radiations qui la traversent.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les éléments essentiels de la modélisation
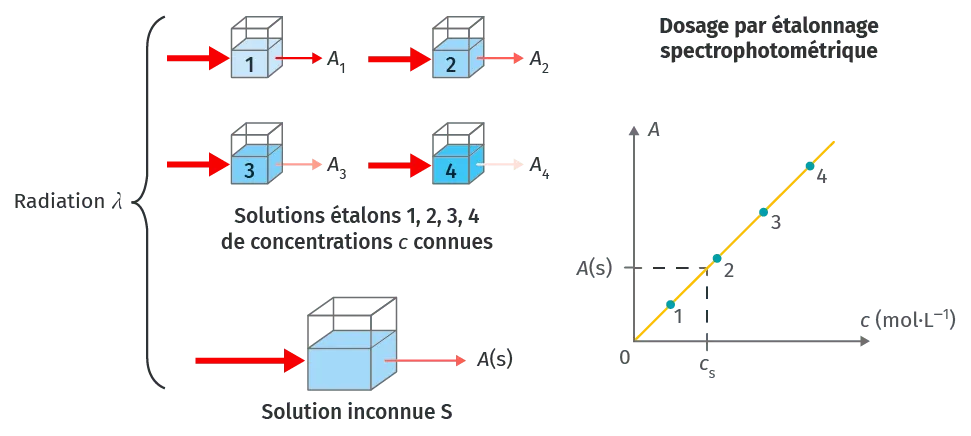
Pour une longueur d'onde donnée, l'absorbance d'une espèce chimique colorée en solution est proportionnelle à la concentration de cette espèce chimique.
La loi de Beer-Lambert s'écrit :
A_{\lambda}=k \cdot c=\epsilon_{\lambda} \cdot l \cdot c
avec A_{\lambda} sans unité, \epsilon_{\lambda} en L·mol-1·cm-1, l en cm et c en mol·L-1.
La loi de Beer-Lambert s'écrit :
A_{\lambda}=k \cdot c=\epsilon_{\lambda} \cdot l \cdot c
avec A_{\lambda} sans unité, \epsilon_{\lambda} en L·mol-1·cm-1, l en cm et c en mol·L-1.
Cette propriété permet de doser une espèce chimique par étalonnage spectrophotométrique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les limites de la modélisation
Les conditions de validité de la loi de Beer-Lambert sont les suivantes :
- les espèces chimiques présentes en solution ne doivent pas réagir ensemble ;
- la solution doit être homogène ;
- la radiation incidente doit être monochromatique ;
- la radiation incidente ne doit pas faire réagir les espèces chimiques en solution ;
- les valeurs d'absorbance ne doivent pas être trop importantes (la valeur 1 est communément admise comme limite).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Réalisez une et reprenez les principales notions du chapitre !
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
