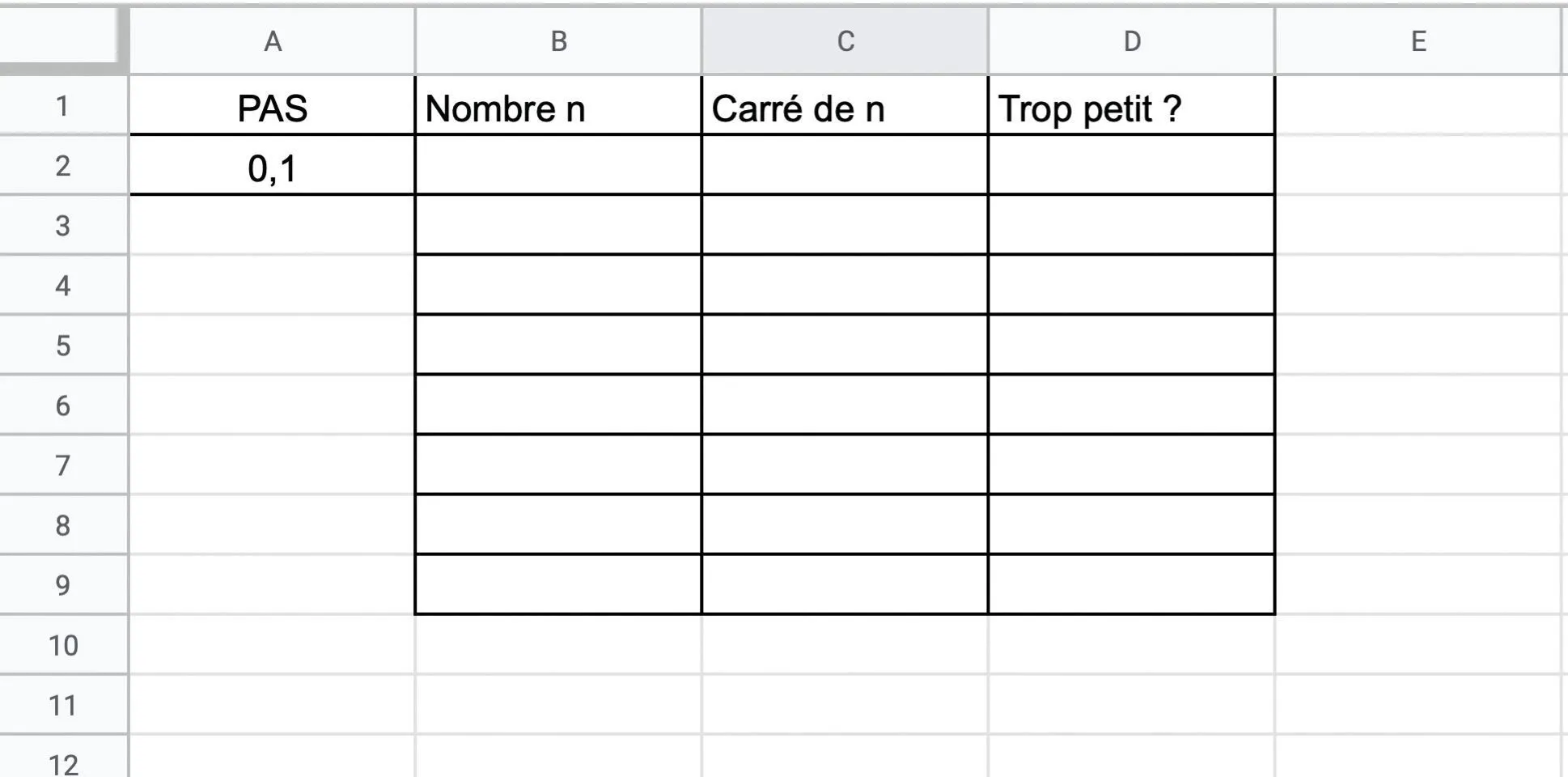
1. Recopier la feuille de calcul. Dans B2, écrire le nombre a trouvé dans la question préliminaire.

2. a. Dans B3, écrire une formule qui permet, lorsqu'elle est étirée vers le bas, d'obtenir tous les nombres entre a et b avec un pas égal à A2.

b. Dans C2, écrire une formule qui permet, lorsqu'elle est étirée vers le bas, d'obtenir les carrés de tous les nombres de la colonne B.

3. En déduire alors un encadrement à 0{,}1 près de \sqrt{2} . Donner la valeur approchée de \sqrt{2} par défaut à 10^{-1} près.

4. Modifer la feuille de calcul pour obtenir une valeur approchée par défaut de \sqrt{2} à 10^{-2} près.

1. On complétera le programme suivant au fur et à mesure.

def RacineDeux(pas) :
  essai = ...
  while ... :
    essai = ...
  return(...)

2. Que représente la variable \bf{pas} dans la définition de la fonction ?

3. Quelle valeur faut-il affecter à la variable \bf{essai} pour l'initialiser à la ligne 2 ?

4. Compléter le critère d'arrêt de la boucle \bf{tant\: que} à la ligne 3.

5. Compléter les lignes 4 et 5 pour obtenir le résultat recherché.

6. À l'aide du programme, déterminer une valeur approchée par défaut de \sqrt{2} à 10^{-1}, puis à 10^{-2} près.

1. a. Tracer la représentation graphique de la fonction f définie pour tout x \in \R par f(x) = x^2 - 2 .

b. Justifier que trouver une valeur approchée de \sqrt{2} revient à trouver une valeur approchée de la solution positive de f(x) = 0 .

c. Sélectionner l'outil Inspecteur de fonction (voir ci-dessous), puis cliquer approximativement sur le point d'intersection, dont l'abscisse est positive, de la courbe avec l'axe des abscisses.


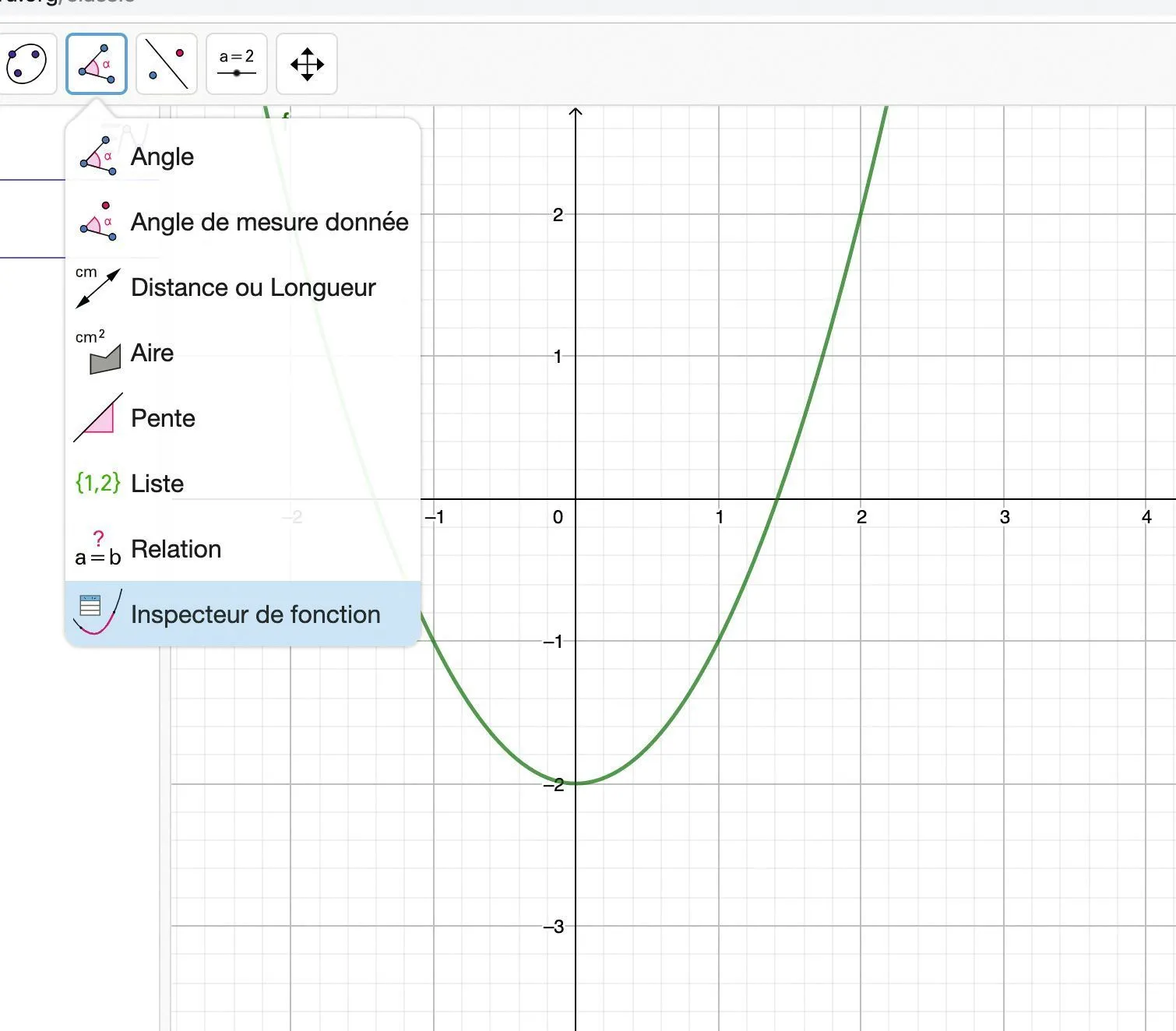
d. Sélectionner l'onglet « points » et entrer la valeur 0{,}1 pour le pas.

2. Quel nombre a-t-on ainsi approché ?

3. Donner une valeur approchée par défaut de \sqrt{2} à 10^{-2} près.