Enseignement scientifique 1re
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Thème 1 : Une longue histoire de la matière
Ch. 1
Les éléments chimiques
Ch. 2
Des édifices ordonnés : les cristaux
Ch. 3
Une structure complexe : la cellule
Thème 2 : Le Soleil, notre source d'énergie
Ch. 4
Le rayonnement solaire
Ch. 5
Le bilan radiatif terrestre
Ch. 6
Énergie solaire et photosynthèse
Ch. 7
Le bilan thermique du corps humain
Thème 3 : La Terre, un astre singulier
Ch. 8
La forme de la Terre
Ch. 9
L'histoire de l’âge de la Terre
Ch. 10
La Terre dans l’Univers
Thème 4 : Son et musique, porteurs d'information
Ch. 11
Le son, phénomène vibratoire
Ch. 12
Musique et nombres
Ch. 13
Le son, une information à coder
Ch. 14
Entendre la musique
Projet Experimental et Numérique
Livret Maths
Annexes
Livret maths 1
S'entraîner au calcul
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Introduction
En sciences, la création de modèles destinés à expliquer notre réalité est toujours allée de pair avec le développement d'outils mathématiques.
Vous trouverez au sein de ce livret maths, tous les outils mathématiques utilisés en classe d'enseignement scientifique.
Vous trouverez au sein de ce livret maths, tous les outils mathématiques utilisés en classe d'enseignement scientifique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Point de cours 1Révisions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
Dans une expression numérique sans parenthèses, on effectue :
- dʼabord les multiplications et les divisions, de gauche à droite ;
- puis les additions et les soustractions, également de gauche à droite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
Dans une expression numérique qui contient des parenthèses, on effectue :
Quand il y a des parenthèses imbriquées, on effectue dʼabord les calculs entre les parenthèses les plus intérieures.
- en priorité les calculs entre les parenthèses ;
- puis on procède comme pour une expression numérique sans parenthèses.
Quand il y a des parenthèses imbriquées, on effectue dʼabord les calculs entre les parenthèses les plus intérieures.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemples
\text{A} = 20 − 2 × 3 + 12 ÷ 6 = 20 − 6 + 2 = 14 + 2 = 16
\text{B} = (3 × (7 − 3)) + 1 = (3×4) + 1 = 12 + 1 = 13
\text{B} = (3 × (7 − 3)) + 1 = (3×4) + 1 = 12 + 1 = 13
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercices
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Effectuez les calculs suivants.
a. 5 \times 9-25 \div 5
b. 7 \times(64-54)
c. 45-30 \div(8-3)
b. 7 \times(64-54)
c. 45-30 \div(8-3)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2 Effectuez les calculs suivants.
a. 5+8-4 \times 3
b. 36 \div 6+7 \times 6
c. 4+63 \div 9+2
b. 36 \div 6+7 \times 6
c. 4+63 \div 9+2
d. 81-11 \times 6 \div 3
e. 40 \div 8+8 \times 8
f. 12 \times 6 \div 8 \times 7
e. 40 \div 8+8 \times 8
f. 12 \times 6 \div 8 \times 7
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3 Effectuez les calculs suivants.
a. (1+4 \times 8)+2
b. 72 \div(16 \div 2)
c. 7 \times 6+(18 \div 9)
b. 72 \div(16 \div 2)
c. 7 \times 6+(18 \div 9)
d. 20-(8 \times 4-20)
e. 35 \div 7 \times(47-12)
f. (15+2) \times 3+4
e. 35 \div 7 \times(47-12)
f. (15+2) \times 3+4
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Point de cours 2Proportionnalité
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
Deux grandeurs sont proportionnelles si les valeurs de l'une sont obtenues en multipliant les valeurs de
l'autre toujours par un même nombre, appelé le coefficient de proportionnalité.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Le prix payé à la station service est proportionnel au volume d'essence mis dans le réservoir du véhicule. Le coefficient de proportionnalité est le prix au litre.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Point de cours 3Représentation de la proportionnalité
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
On peut toujours représenter une situation de proportionnalité à l'aide d'un tableau de proportionnalité.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Chez le primeur, 5 kg de pommes coûtent 6 euros. On peut représenter cette situation à l'aide d'un tableau.
| Masse (kg) | 5 | 15 |
| Prix (euros) | 6 | 18 |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
Une situation de proportionnalité est modélisée par une fonction linéaire et, dans un repère, elle est
représentée par une droite qui passe par l'origine de ce repère. Le coefficient de proportionnalité correspond alors au coefficient directeur de cette droite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
Un pourcentage traduit une proportion. C'est une fraction dont le dénominateur vaut 100. Déterminer un
pourcentage revient à calculer cette proportion.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Dans une classe de 25 élèves il y a 7 filles. Pour déterminer le pourcentage de filles, on peut remplir un tableau de proportionnalité. On trouve 28 % :

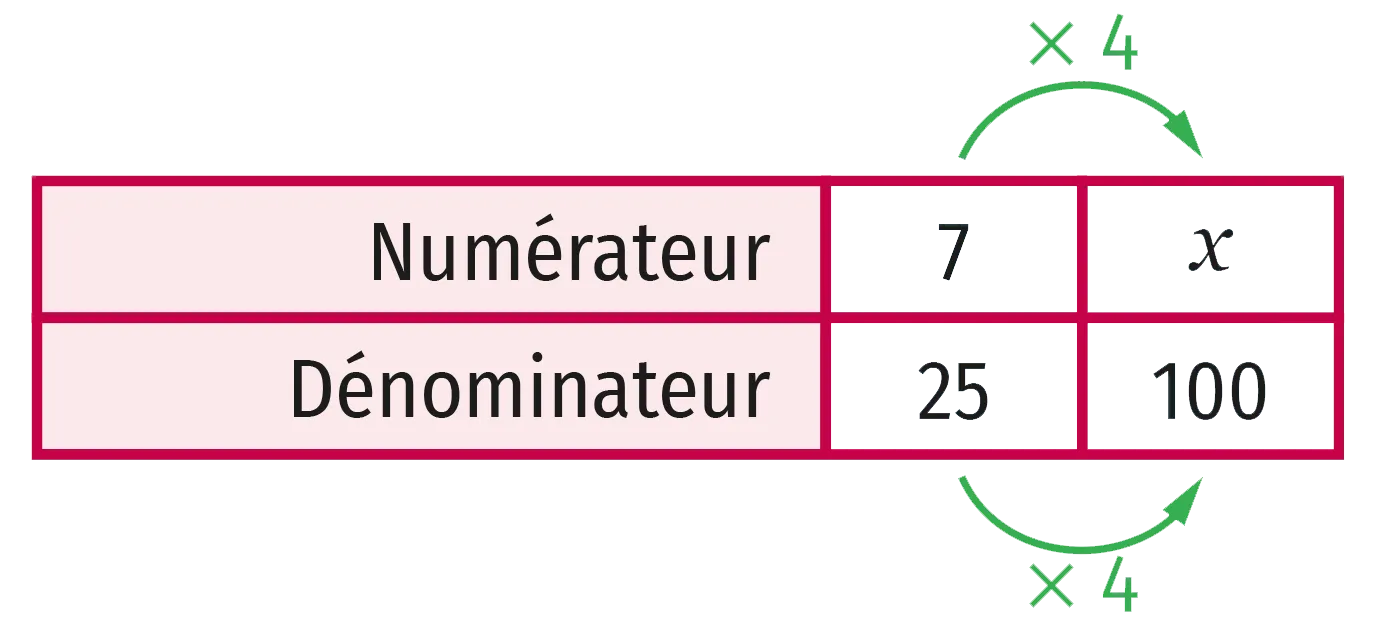
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercices
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4 Identifiez les grandeurs proportionnelles.
a. La longueur du côté dʼun carré et son périmètre.
b. Le nombre de sommets dʼun polygone et la somme de ses angles.
b. Le nombre de sommets dʼun polygone et la somme de ses angles.
c. La longueur du côté dʼun carré et son aire.
d. Le nombre de lettres dans un mot et le nombre des voyelles dans le mot.
d. Le nombre de lettres dans un mot et le nombre des voyelles dans le mot.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5 Complétez les tableaux de proportionnalité
suivants.
a.
b.
c.
d.
e.
f.
| 3 | 7 | 10 | 13 | \times 7 |
b.
| 5 | 9 | 2 | 6 | \times 0{,}5 |
c.
| 1 | 3{,}5 | 7 | 2{,}5 | \times \frac{2}{5} |
d.
| 1 | 2 | 10 | 6 | \times |
| 6 |
e.
| 5 | 20 | \times | ||
| 8 | 12 | 16 |
f.
| 2 | 5{,}5 | 7{,}5 | \times | |
| 0{,}55 | 101{,}5 |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6 Si jʼachète 3 places de cinéma, je paie 5 €. Si jʼen
achète 10, ça me coûte 15 €, donc :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7 La classe de 2de 4.
La classe de 2de 4 du lycée Duruy est composée de 38 élèves, dont 16 filles.
Quel est le pourcentage de filles en 2de 4 ?
Quel est le pourcentage de filles en 2de 4 ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8 Le laiton jaune est un alliage métallique de cuivre
et de zinc. Un morceau de 650 g de laiton jaune contient 403 g de cuivre.
a. Quel est le pourcentage de cuivre contenu dans ce morceau de laiton jaune ?
b. Quel est le pourcentage de zinc contenu dans ce morceau de laiton jaune ?
b. Quel est le pourcentage de zinc contenu dans ce morceau de laiton jaune ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9 Effectuez les calculs suivants.
Sur une carte dʼéchelle \dfrac{1}{200\;000} , la maison dʼAbdel est
à 1,25 cm de son collège.
Quelle est la distance réelle entre son collège et sa maison en ligne droite ?
Quelle est la distance réelle entre son collège et sa maison en ligne droite ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10 Quel est le prix de
13 pralinés ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Point de cours 4Calcul littéral
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
- Une expression littérale est une expression dans laquelle des lettres représentent des nombres. Ces lettres sont appelées des variables.
- Deux expressions littérales sont « égales » si elles donnent le même résultat pour n'importe quelles valeurs attribuées aux lettres de l'expression.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
Identités remarquables. Pour tous nombres a et b, on a :
| forme factorisée | forme développée | |
| (a+b)^{2} | = | a^{2}+2 a b+b^{2} |
| (a-b)^{2} | = | a^{2}-2 a b+b^{2} |
| (a+b)(a-b) | = | a^{2}-b^{2} |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
- 3 x+8=4 x(2-x) est une expression littérale.
Quels que soient les nombres a et b, on a : (a-b)^{2}=a^{2}-2 a b+b^{2}. - \begin{array}{l}{4 x(2-x)=4 x \times 2-4 x \times x} \\ {4 x(2-x)=8 x-4 x^{2}}\end{array}
- \begin{array}{l}{3-2 z(5 z-4)=3-2 z \times 5 z-2 z \times(-4)} \\ {3-2 z(5 z-4)=3-10 z^{2}+8 z}\end{array}
- (2 x-5)(3+4 x)=6 x+8 x^{2}-15-20 x
- Soit \text{A}=(4+3 z)(2 z+1)-(5+7 z)(z+3)
\begin{array}{l}{\text{A}=8 z+4+6 z^{2}+3 z-\left(5 z+15+7 z^{2}+21 z\right)} \\ {\text{A}=z^{2}-15 z-11}\end{array} - (3 x+7)^{2}=9 x^{2}+42 x+49
- (5-2 y)^{2}=25-20 y+4 y^{2}
- (z+3)(z-3)=z^{2}-9
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercices
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
11 Périmètre d'un cercle.
Le lien entre le diamètre d et le rayon r d'un cercle est
donné par la formule d = 2r.
Pour calculer le périmètre P, on applique la formule P=2 \pi r. Complétez le tableau suivant.
Pour calculer le périmètre P, on applique la formule P=2 \pi r. Complétez le tableau suivant.
|
r en cm |
d en cm |
Valeur arrondie |
|
5,0 | ||
|
8,0 | ||
|
4,0 | ||
|
7,5 | ||
|
2,5 |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
12 Calculez le volume de
ce parallélépipède rectangle pour :
a. z = 2
b. z = 8
c. z = 4\text{,}5
b. z = 8
c. z = 4\text{,}5

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
13 Distance de freinage.
À lʼautoécole, on apprend que « la distance de freinage d est le centième du carré de la vitesse v ».
Exprimez cette règle par une formule.
Exprimez cette règle par une formule.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
14 Factorisez les expressions suivantes.
a. 3 x+9
b. 27-9 y
c. 12 x+18 y
b. 27-9 y
c. 12 x+18 y
d. 13 x+2 x
e. x y+4 y
f. x^{2}+3 x
e. x y+4 y
f. x^{2}+3 x
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
15 Un paquetage.
a. De quelle longueur de
ficelle a-t-on besoin pour ficeler le paquet ci-contre de longueur 40 cm, de largeur 30 cm et de hauteur 10 cm, de la façon indiquée, sans compter les nœuds ?
b. Donnez la longueur de la ficelle en fonction des dimensions L, l et h du paquet.
b. Donnez la longueur de la ficelle en fonction des dimensions L, l et h du paquet.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
16 Éliminez toutes les parenthèses et réduisez les
expressions au maximum.
a. 3,5 e+2,2 e+e \times 2
b. c \times(3+11)+c+2
c. 1\text{,}7-(2\text{,}4 \times a-2\text{,}4)
d. (2 a+3) \times 3+8 a
b. c \times(3+11)+c+2
c. 1\text{,}7-(2\text{,}4 \times a-2\text{,}4)
d. (2 a+3) \times 3+8 a
e. (x+y) \times(z+4)
f. 3-(-6+a) \times 20
g. (a+1) \times(b+1)-2
h. (a-3) \times(a+1)-4 a
f. 3-(-6+a) \times 20
g. (a+1) \times(b+1)-2
h. (a-3) \times(a+1)-4 a
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17 Réduisez les expressions au maximum.
a. (7+a) \times(b+1)
b. (3\text{,}2-x) \times(2+x)
c. (y-1\text{,}5) \times(y-1)
d. (a b+1) \times(a+b)
e. -1-a \times(3-a)
f. (x+4)^{2}
g. (x-4)^{2}
b. (3\text{,}2-x) \times(2+x)
c. (y-1\text{,}5) \times(y-1)
d. (a b+1) \times(a+b)
e. -1-a \times(3-a)
f. (x+4)^{2}
g. (x-4)^{2}
h. (x+4) \times(x-4)
i. (-x-4) \times(-x-4)
j. (-4-4) \times(-x-x)
k. (a+b) \times(a-c)
l. (-2 \times a) \times(a+4)
m. (x+2)^{3}
n. (x-2)^{3}
i. (-x-4) \times(-x-4)
j. (-4-4) \times(-x-x)
k. (a+b) \times(a-c)
l. (-2 \times a) \times(a+4)
m. (x+2)^{3}
n. (x-2)^{3}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Point de cours 5Équations à une inconnue
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
- Résoudre une équation, c'est trouver toutes les valeurs que l'on peut donner à x pour que l'égalité soit vraie. Ces valeurs sont appelées solutions de l'équation.
- Méthode de résolution : on applique des opérations successives aux deux membres de lʼéquation dans le but dʼavoir lʼinconnue dʼun seul côté. On obtient ainsi la valeur de lʼinconnue. On vérifie que chaque valeur trouvée est bien solution de lʼéquation.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
Un produit est nul si et seulement si au moins lʼun de ses facteurs est nul.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
- 3 \times 2+2=8
2+6=8
Donc avec x = 2, l'égalité 3x + 2 = x + 6 est vérifiée. 2 est une solution de cette équation. - 5 x+6=8-2 x
7x + 6 = 8
7x = 2
x=\dfrac{2}{7}
Si on remplace x par cette valeur alors l'égalité de départ est bien vérifiée. - (3 x-8)(x+7)=0 est une équation produit nul
d'inconnue x.
Soit (3 x-8)=0 ou (x+7)=0
Soit x=\dfrac{8}{3} ou x = -7
Cette équation admet donc deux solutions :
\dfrac{8}{3} et -7.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercices
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
18 Résolvez les équations suivantes.
a. 3 x+7=-13-2 x
b. 3(2 x-3)=27
c. 6(x-3)=3 x
b. 3(2 x-3)=27
c. 6(x-3)=3 x
d. 2 x-9=(5 x+7) \times(-3)
e. 0\text{,}5 x-2\text{,}6=3 x+1\text{,}4
f. 8 x=(5 x-3) \times(-0\text{,}2)
e. 0\text{,}5 x-2\text{,}6=3 x+1\text{,}4
f. 8 x=(5 x-3) \times(-0\text{,}2)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19 Résolvez les équations suivantes.
a. 6 x-4=3 \times(2-x)
b. 2 \times \pi \times x=10
c. -\dfrac{1}{2}=\dfrac{1}{4} x+5
b. 2 \times \pi \times x=10
c. -\dfrac{1}{2}=\dfrac{1}{4} x+5
d. 0\text{,}5 x+2=3 x-8
e. 2 x=3 \times \pi
f. \dfrac{1}{3} x+\dfrac{2}{3} x=5+2 x
e. 2 x=3 \times \pi
f. \dfrac{1}{3} x+\dfrac{2}{3} x=5+2 x
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20 Résolvez les équations suivantes.
a. (x+1) \times(x-2)=0
b. (3 x+2) \times(-4 x+5)=0
c. x^{2}-2 x+1=(x+1)(-2 x+7)
b. (3 x+2) \times(-4 x+5)=0
c. x^{2}-2 x+1=(x+1)(-2 x+7)
d. (3 x+2)(-4 x+5)=0
e. (2 x+5)^{2}=0
e. (2 x+5)^{2}=0
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21 Aires et périmètres.

a. Déterminez la valeur de x pour laquelle les deux rectangles ont la même aire.
b. Déterminez la valeur de x pour laquelle les deux rectangles ont le même périmètre.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22 Périmètre d'une figure géométrique.

Aude veut former la figure illustrée ci-dessus avec un fil métallique de 96 cm de longueur.
Quelle est la valeur maximale que l'on peut choisir pour x ?
Quelle est la valeur maximale que l'on peut choisir pour x ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
