Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
1. Constitution et transformations de la matière
Ch. 1
Composition chimique d'un système
Ch. 2
Composition chimique des solutions
Ch. 3
Évolution d'un système chimique
Ch. 4
Réactions d'oxydoréduction
Ch. 5
Détermination d'une quantité de matière par titrage
Livret Bac : Thème 1
Ch. 6
De la structure à la polarité d'une entité
Ch. 7
Interpréter les propriétés d’une espèce chimique
Ch. 8
Structure des entités organiques
Ch. 9
Synthèse d'espèces chimiques organiques
Ch. 10
Conversions d'énergie au cours d'une combustion
Livret Bac : Thème 1 bis
2. Mouvement et interactions
Ch. 11
Modélisation d'interactions fondamentales
Ch. 12
Description d'un fluide au repos
Ch. 13
Mouvement d'un système
Livret Bac : Thème 2
3. L'énergie, conversions et transferts
Ch. 14
Études énergétiques en électricité
Ch. 15
Études énergétiques en mécanique
Livret Bac : Thème 3
4. Ondes et signaux
Ch. 16
Ondes mécaniques
Ch. 17
Images et couleurs
Ch. 18
Modèles ondulatoire et particulaire de la lumière
Livret Bac : Thème 4
Méthode
Fiches méthode
Fiche méthode compétences
Annexes
Chapitre 15
Activité 3 - Activité expérimentale
80 min
Étude d'un pendule avec un smartphone
10 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Problématique de l'activité
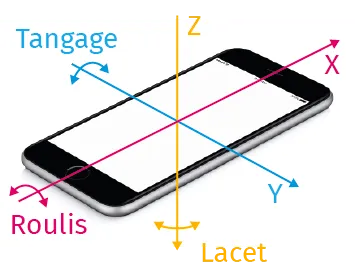
Un smartphone est doté de multiples capteurs. L'un d'entre eux, le gyromètre,
permet de déterminer très précisément les vitesses angulaires de l'appareil
autour de trois axes.
Comment exploiter ce capteur pour l'étude des oscillations d'un pendule ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 1Le modèle du pendule simple
Le zoom est accessible dans la version Premium.
Un pendule simple est une masse suspendue à un fil supposé inextensible et dont on néglige la masse, et qui oscille autour de sa position d'équilibre \mathrm{M}_{0}, point le plus bas de sa trajectoire. L'étude énergétique du pendule simple nécessite de déterminer à chaque instant :
La relation entre vitesse angulaire \omega (rad·s-1) et la vitesse linéaire v (m·s‑1) est donnée par : v=\omega \cdot l avec l la longueur du fil (m).
- l'énergie potentielle E_{\mathrm{p}}=m \cdot g \cdot z de l'objet suspendu, z étant à un instant donné l'altitude de l'objet de masse m par rapport à \mathrm{M}_{0}\:;
- l'énergie cinétique E_{\mathrm{c}}=\dfrac{1}{2} m \cdot v^{2}\:;
- v étant la vitesse de cet objet.
La relation entre vitesse angulaire \omega (rad·s-1) et la vitesse linéaire v (m·s‑1) est donnée par : v=\omega \cdot l avec l la longueur du fil (m).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 2Application avec Phyphox
Suspendre un smartphone en position verticale et faire l'acquisition de sa vitesse angulaire
\omega. Une acquisition de qualité exige d'éviter tout mouvement de rotation de
l'appareil sur lui-même. Utiliser la fonction « gyroscope » de Phyphox. Dans les « paramètres », cocher la case « départ retardé » et prendre une durée de mesures de 10 à 15 s environ. L'exportation des données se fait au format CSV, tabulation, virgule décimale.
Retrouvez l'application .
Retrouvez l'application .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 3L'exploitation des données sous Regressi
- Repérer l'axe de rotation principal (\omega_{x}, \omega_{y} ou \omega_{z}).
- Détermination de l'angle de rotation theta : l'angle de rotation theta a une valeur nulle quand le smartphone passe au plus bas de sa trajectoire à l'instant où la vitesse angulaire passe par un maximum. Une fois cet instant repéré, supprimer toutes les données qui le précèdent. Créer alors la grandeur calculée theta (cocher la méthode d'Euler exprimée en radian) :
theta(i) = theta[i-1] + (\omega)*(Time[i]-Time[i-1]) avec theta(0) = 0. - Il est dès lors possible de créer les grandeurs E_{\mathrm{c}} et E_{\mathrm{pp}}, et de tracer leur courbe représentative en fonction du temps.
Téléchargez le logiciel .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions
Compétence(s)
REA : Acquérir des données grâce à des
capteurs
VAL : Traiter, exploiter, modéliser numériquement un ensemble de mesures
VAL : Traiter, exploiter, modéliser numériquement un ensemble de mesures
1. Doc. 1 Exprimer l'énergie cinétique E_{\mathrm{c}} d'un pendule en fonction de la masse suspendue m, de la longueur l et de la vitesse angulaire \omega. Exprimer l'énergie potentielle E_{\mathrm{pp}} en fonction de m, l et de l'intensité du champ de pesanteur g.
2. Doc. 2 Proposer un montage permettant de faire l'acquisition de la vitesse angulaire du pendule à partir d'un smartphone. Après validation, faire cette acquisition.
3. Doc. 3 Ouvrir le fichier des données sous Regressi et créer les grandeurs énergie cinétique E_{\mathrm{c}}, angle de rotation theta, énergie potentielle E_{\mathrm{pp}} et énergie mécanique E_{\mathrm{m}}=E_{\mathrm{c}}+E_{\mathrm{p}}, puis visualiser leurs représentations graphiques en fonction du temps.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
4. L'énergie mécanique est-elle conservée au cours du temps ? Justifier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Synthèse de l'activité
Quels sont les atouts d'un smartphone pour faire l'acquisition des données dans l'étude énergétique d'un pendule ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah