Mathématiques Terminale Spécialité
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Rappels de première
Algèbre et géométrie
Ch. 1
Combinatoire et dénombrement
Ch. 2
Vecteurs, droites et plans de l’espace
Ch. 3
Orthogonalité et distances dans l’espace
Analyse
Ch. 4
Suites
Ch. 5
Limites de fonctions
Ch. 6
Continuité
Ch. 7
Compléments sur la dérivation
Ch. 8
Logarithme népérien
Ch. 9
Fonctions trigonométriques
Ch. 10
Primitives - Équations différentielles
Ch. 11
Calcul intégral
Probabilités
Ch. 12
Loi binomiale
Ch. 13
Sommes de variables aléatoires
Ch. 14
Loi des grands nombres
Annexes
Exercices transversaux
Grand Oral
Apprendre à démontrer
Cahier d'algorithmique et de programmation
Chapitre 6
Cours 2
Le théorème des valeurs intermédiaires
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ACas général
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Théorème des valeurs intermédiaires
Si f est continue sur [a\,;b] alors, pour tout réel k compris entre f(a) et f(b), l'équation f(x) = k admet au moins une solution dans [a\,;b].
Autrement dit, tout réel k compris entre f(a) et f(b) admet au moins un antécédent par f dans [a\,;b].
Autrement dit, tout réel k compris entre f(a) et f(b) admet au moins un antécédent par f dans [a\,;b].

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On peut aussi utiliser des limites si f n'est pas définie en a ou b ou bien encore des limites en -\infty ou en +\infty.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le théorème des valeurs intermédiaires indique s'il existe une solution. Il ne
permet pas un calcul effectif de celle‑ci.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
Voir exercice p. 209.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode - 3
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Soit f la fonction définie sur \mathbb{R} par f: x \mapsto \mathrm{e}^{3 x}+x.
Montrer que, pour tout k \in\left[1\,;1+\mathrm{e}^{3}\right], l'équation f(x) = k admet au moins une solution dans [0\,;1].
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Vérifier d'abord que la fonction est continue sur l'intervalle considéré.
- Calculer f(a) puis f(b).
- Appliquer le théorème des valeurs intermédiaires.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
f est continue sur \mathbb{R} donc sur [0\,;1] comme somme de fonctions continues sur \mathbb{R}. Or f(0)=1 et f(1)=1+\mathrm{e}^{3}. D'après le théorème des valeurs intermédiaires, pour tout k appartenant à l'intervalle \left[1\,;1+\mathrm{e}^{3}\right], l'équation f(x) = k admet au moins une solution dans [0\,;1].
Pour s'entraîner
Exercices et p. 202
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BCas des fonctions strictement monotones
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Corollaire
Si f est continue et strictement monotone sur [a\,;b] alors, pour tout réel k compris entre f(a) et f(b), l'équation f(x) = k admet une unique solution dans [a\,;b].
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On peut aussi étendre ce corollaire aux intervalles ouverts en utilisant les limites.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
Voir exercice p. 206.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode - 4
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Soit la fonction f: x \mapsto x^{3}-3 x^{2}-1 définie sur \mathbb{R}.
Quel est le nombre de solutions de l'équation f(x) = 4 sur \mathbb{R} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- On détermine f^\prime et son signe.
- On dresse le tableau de variations de f.
- On se sert des extremums pour localiser les intervalles où peuvent se trouver les solutions.
- On applique le corollaire du théorème des valeurs intermédiaires sur ces intervalles.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
f est une fonction polynôme, elle est donc continue sur \mathbb{R}.
Pour tout x \in \mathbb{R}, f^{\prime}(x)=3 x^{2}-6 x=3 x(x-2).

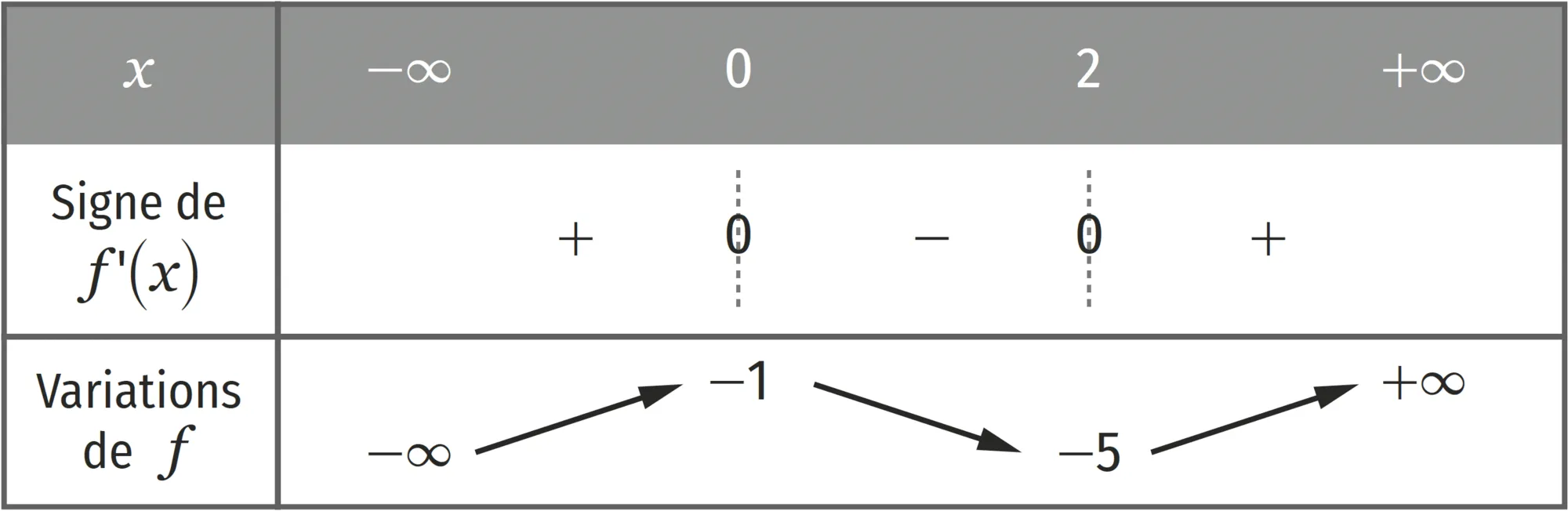
Sur ]-\infty\,;2], le maximum de f vaut -1 donc f(x) = 4 n'a pas de solution sur cet intervalle.
Sur [2\,;+\infty[, f est continue et strictement croissante. 4 \in[-5\,;+\infty[ donc, d'après le corollaire du théorème des valeurs intermédiaires ci‑dessus, il existe un unique a \in[2\,;+\infty[ tel que f(a) = 4.
Donc l'équation f(x) = 4 n'admet qu'une seule solution sur \mathbb{R}.
Pour tout x \in \mathbb{R}, f^{\prime}(x)=3 x^{2}-6 x=3 x(x-2).


Sur ]-\infty\,;2], le maximum de f vaut -1 donc f(x) = 4 n'a pas de solution sur cet intervalle.
Sur [2\,;+\infty[, f est continue et strictement croissante. 4 \in[-5\,;+\infty[ donc, d'après le corollaire du théorème des valeurs intermédiaires ci‑dessus, il existe un unique a \in[2\,;+\infty[ tel que f(a) = 4.
Donc l'équation f(x) = 4 n'admet qu'une seule solution sur \mathbb{R}.
Pour s'entraîner
Exercices et p. 203
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
