f désigne une fonction continue sur \mathbb{R}. Déterminer, en justifiant, si l'équation f(x) = 0 admet au moins une solution sur [1\,; 2] lorsque :

1. f(1) \times f(2)>0.

2. f(1) \times f(2)=0.

3. f(1) \times f(2) \lt 0.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Flash

f est une fonction continue sur \mathbb{R} dont voici le tableau de variations.

maths spé - chapitre 6 - continuité - exercice 59

Combien de solutions dans \mathbb{R} les équations suivantes admettent‑elles ?
f(x)=0 ; f(x)=3 ; f(x)=10.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

60
[Calculer.]
Soit la fonction f: x \mapsto x^{3}+2 x^{2}-3 x-1 définie sur \mathbb{R}.
Quel est le nombre exact de solutions de l'équation f(x) = 0 sur \mathbb{R} ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

61
[Calculer.]
Soit la fonction g: x \mapsto \mathrm{e}^{-x}-3 définie sur \mathbb{R}.
Démontrer que l'équation g(x) = 0 admet une unique solution sur \mathbb{R}.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

[Calculer.]
On considère la fonction f définie sur \mathbb{R} par f(x)=x \mathrm{e}^{-x}+1.

1. Démontrer que l'équation f(x) = 0 admet une unique solution \alpha sur \mathbb{R}.

2. Déterminer un encadrement de \alpha à 10^{-1} près.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

63
[Calculer.]
Soit la fonction f: x \mapsto x^{3}+x+1 définie sur \mathbb{R}.

1. Dresser le tableau de variations de f sur \mathbb{R}.

Cliquez pour accéder à une zone de dessin

2. Démontrer que l'équation f(x) = 0 admet une unique solution sur [-1\,;0].

3. Trouver toutes les valeurs du réel k pour que l'équation f(x) = k admette une unique solution sur [-1\,;0].

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

64
[Calculer.]
Soit la fonction h: x \mapsto \mathrm{e}^{x}+x définie sur \mathbb{R}.

1. Montrer que l'équation h(x) = 0 admet une unique solution réelle.

2. En proposer un encadrement d'amplitude 0{,}1.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

65
[Calculer.]
On considère la fonction f définie sur \mathbb{R} par :

f(x)=(3 x-4) \mathrm{e}^{-x}.

1. Démontrer que l'équation f(x) = 0 admet une unique solution \alpha sur [0\,;4].

2. Déterminer un encadrement de \alpha à 10^{-3} près.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

66
[Calculer.]
Soient deux fonctions f_{1}: x \mapsto \mathrm{e}^{x} et f_{2}: x \mapsto-x+2 définies sur \mathbb{R}.
Démontrer que l'équation f_{1}(x)=f_{2}(x) admet une unique solution sur [0\,;1].

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

[Chercher.]
Montrer que l'équation 2 \mathrm{e}^{2 x}=\sqrt{5-x} admet une unique solution \alpha sur ]-\infty\,;5] et que \alpha \in[0\,;1].

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

68
[Chercher.]
Montrer que l'équation 2(x-1) \mathrm{e}^{x-1}=x^{2} admet une unique solution \alpha sur \mathbb{R} et que \alpha \in[1{,}7\,; 1{,}8].

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

[Raisonner.]
Soit n un entier naturel. On considère une fonction polynôme de degré n : f: x \mapsto a_{n} x^{n}+\ldots+a_{1} x+a_{0} où a_{i} \in \mathbb{R} pour tout i de 0 à n et a_{n} \neq 0.

Démontrer que toute fonction polynôme de degré impair admet au moins une racine réelle.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

70
[Communiquer.]

Voici un programme écrit en Python.
Expliquer, en justifiant, à quel problème permet de répondre ce programme.

Code Python : fonction fct() utilisant la méthode de dichotomie pour trouver une racine de la fonction f(x) = exp(x) - 2.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

71
[Chercher.]
On considère une fonction f continue sur l'intervalle [a\,;b]. Compléter ce code Python pour obtenir en retour un encadrement à eps près d'une solution de f(x) = 1.

def fct(a, b, eps):
	while b - a > eps:
		m = (a + b)/2
		if ...:
			b = ...
		else:
			a = ...
	return a, b

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

72
[Raisonner.]
On considère la fonction f définie sur \mathbb{R} par :

f(x)=(x+2) \mathrm{e}^{-0,5 x}.

Un logiciel de calcul formel permet d'obtenir le résultat suivant.

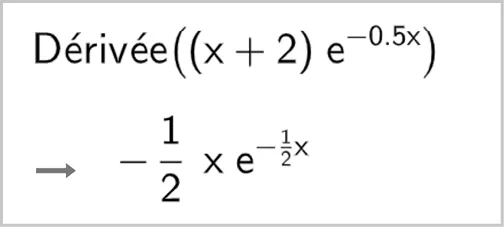
Image d'une formule mathématique montrant le calcul de la dérivée de (x+2)e^-0.5x.

1. Démontrer que l'équation f(x) = 0{,}1 admet une unique solution \alpha sur [0\,; 50].

2. En donner un encadrement de \alpha à 10^{-2} près.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Démo

[Raisonner.]
On souhaite démontrer la proposition suivante : « Si f est continue et strictement monotone sur \mathrm{I}=[a\,;b] alors, pour tout k compris entre f(a) et f(b), l'équation f(x) = k admet une unique solution dans \text{I}. »

1. Démontrer qu'il existe au moins une solution sur \text{I} à l'équation f(x) = k.

2. Raisonnons par l'absurde et supposons qu'il existe deux réels distincts \alpha et \beta dans \text{I} tels que f(\alpha)=f(\beta)=k.
En utilisant la stricte monotonie de f, terminer la démonstration de la proposition.

Afficher la correction

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.