Mathématiques Terminale Spécialité
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Rappels de première
Algèbre et géométrie
Ch. 1
Combinatoire et dénombrement
Ch. 2
Vecteurs, droites et plans de l’espace
Ch. 3
Orthogonalité et distances dans l’espace
Analyse
Ch. 4
Suites
Ch. 5
Limites de fonctions
Ch. 6
Continuité
Ch. 7
Compléments sur la dérivation
Ch. 8
Logarithme népérien
Ch. 9
Fonctions trigonométriques
Ch. 10
Primitives - Équations différentielles
Ch. 11
Calcul intégral
Probabilités
Ch. 12
Loi binomiale
Ch. 13
Sommes de variables aléatoires
Ch. 14
Loi des grands nombres
Annexes
Exercices transversaux
Grand Oral
Apprendre à démontrer
Cahier d'algorithmique et de programmation
Chapitre 6
Entraînement 1
Notion de continuité
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
47
Flash
Si \lim \limits_{\substack{x \rightarrow 3 \\ x>3}} f(x)=\lim \limits_{\substack{x \rightarrow 3 \\ x\lt3}} f(x), peut‑on conclure que f est continue en 3 ? Justifier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
48
Flash
Soient f et g deux fonctions continues sur \text{I}.
1. La fonction f + f \times g est‑elle continue sur \text{I} ?
2. La fonction (f-g)(f+g) est‑elle continue sur \text{I} ?
3. La fonction \frac{f-g}{f+g} est‑elle continue sur \text{I} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
46
Flash
Parmi les fonctions suivantes, lesquelles sont continues en 0 ? Justifier.
1. f: x \mapsto x \mathrm{e}^{x}
2. g: x \mapsto \sqrt{x}
3. h: x \mapsto \frac{1}{x}
4. k: x \mapsto \frac{x}{x+1}
5. m: x \mapsto x^{3}+\sqrt{x}
6. n: x \mapsto \frac{\mathrm{e}^{x}}{\mathrm{e}^{x}+1}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
49
[Représenter.]
La partie entière d'un réel x, notée \mathrm{E}(x), est le nombre entier relatif n tel que n \leqslant x \lt n+1.
1. Calculer \mathrm{E}(3{,}4), \mathrm{E}(2) et \mathrm{E}(-4{,}6).
2. Tracer la représentation graphique de la fonction \mathrm{E}: x \mapsto \mathrm{E}(x) sur [-5\,; 5].
Cliquez pour accéder à une zone de dessin
3. Que peut‑on conjecturer graphiquement sur la continuité de la fonction \mathrm{E} ?
4. Calculer \lim \limits_{\substack{x \rightarrow 1 \\ x >1}} \mathrm{E}(x) et \lim \limits_{\substack{x \rightarrow 1 \\ x \lt 1}} \mathrm{E}(x). Conclure.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
50
[Raisonner.]
Justifier la continuité de la fonction f: x \mapsto \frac{\mathrm{e}^{x} \sqrt{x}}{x^{2}+1} sur \mathrm{I}=[0\,; +\infty[.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
51
[Modéliser.]
On souhaite utiliser GeoGebra pour étudier la continuité en 0 de la fonction f définie par :
1. Recopier et valider les lignes suivantes sur le logiciel.

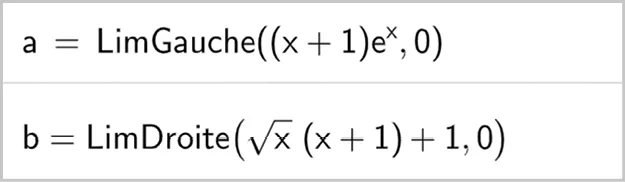
2. Que peut‑on en conclure ?
f: x \mapsto\left\{\begin{array}{r}(x+1) \mathrm{e}^{x} \text { si } x \lt 0 \\ 1 \text { si } x=0 \\ \sqrt{x}(x+1)+1 \text { si } x \lt 0\end{array}\right..
1. Recopier et valider les lignes suivantes sur le logiciel.

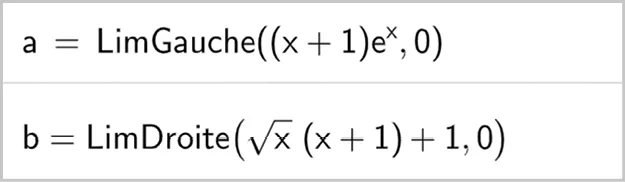
2. Que peut‑on en conclure ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
52
Démo
[Raisonner.]
On considère la fonction f: x \mapsto \sqrt{x} définie pour x \in[0\,;+\infty]. Montrer que f est continue en 0 sans être dérivable en 0.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
53
Démo
[Raisonner.]
Soit f: x \mapsto|x| définie sur \mathbb{R}. Montrer que f est continue en 0 sans être dérivable en 0.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
54
[Calculer.]
Trouver la valeur de k telle que la fonction définie par f: x \mapsto\left\{\begin{aligned} x^{2}+\mathrm{e}^{x-1} & \text { si } x \leqslant 1 \\ x+k & \text { si } x>1 \end{aligned}\right. soit continue sur \mathbb{R}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
55
[Raisonner.]
Justifier la continuité de la fonction f définie sur ] 1\,;+\infty[ par f(x)=x-\frac{1}{x-1}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
56
[Raisonner.]
Justifier la continuité de la fonction f définie sur \mathbb{R} par f(x)=\mathrm{e}^{|x|}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
57
[Communiquer.]
Justifier la continuité de f: x \mapsto 1-x^{2}+\sqrt{1-x^{2}} sur l'intervalle [-1\,; 1].
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
