Méthode par dichotomie

Soit f la fonction définie sur \mathbb{R} par f(x)=\mathrm{e}^{0,5 x}+x^{2}-4. On veut déterminer un encadrement d'une solution \alpha de l'équation f(x) = 0 sur [0\,; 2].
La dichotomie consiste à partager l'intervalle [a\,; b] en deux. On calcule m=\frac{a+b}{2}.
Il y a alors deux possibilités : soit f(a) \times f(m) \lt 0, soit f(m) \times f(b) \lt 0. On choisit le sous‑intervalle où il y a le changement de signe car il contient \alpha et on poursuit.
Ici, a = 0 et b = 2 donc m = 1.
f(a) \times f(m)>0 donc f(a) et f(m) ont le même signe donc \alpha \notin[a\,; m].
f(m) \times f(b) \lt 0 donc f(m) et f(b) sont de signes contraires donc \alpha \in[m\,; b]. Questions préliminaires :
1. Étudier le sens de variation de f sur [0\,; 2].

2. En déduire que f(x) = 0 admet une unique solution \alpha sur [0\,; 2].

À l'aide d'un tableur, on construit ce tableau. (Fichier téléchargeable

ici

.)


1. Quelle formule doit‑on entrer en E2 et F2 pour obtenir respectivement l'image de b par f et l'image de m par f ?

2. En utilisant la fonction SI(test ; valeur_si_vrai ; valeur_si_faux), quelle formule doit‑on entrer en A3 et B3 pour appliquer la méthode de dichotomie ?

3. a. Recopier les formules vers le bas et la droite pour obtenir un résultat semblable à celui‑ci :


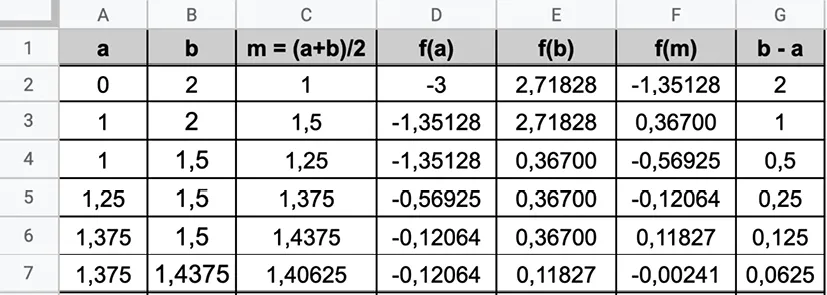
b. Continuer jusqu'à déterminer un encadrement de \alpha à 10^{-4} près.

1. Écrire sous Python une fonction retournant l'expression f(x).

2. Compléter la fonction dichotomie qui retourne un encadrement de \alpha avec une précision epsilon donnée.

from math import *
def f(x):
	return ...

def dichotomie(a, b, epsilon):
	while b - a > epsilon:
		m = (a + b)/2
		if f(a)*f(m) "= ... :
			b = ...
		else:
			a = ...
	return a, b

3. Donner alors un encadrement à 10^{-4} près de \alpha.